Menu Close

1-calculate-U-n-0-1-ln-x-ln-1-x-n-dx-n-gt-0-2-find-nature-of-U-n-and-nU-n-

Tinku Tara 0 Comments
Pin




Question Number 94340 by mathmax by abdo last updated on 20/May/20
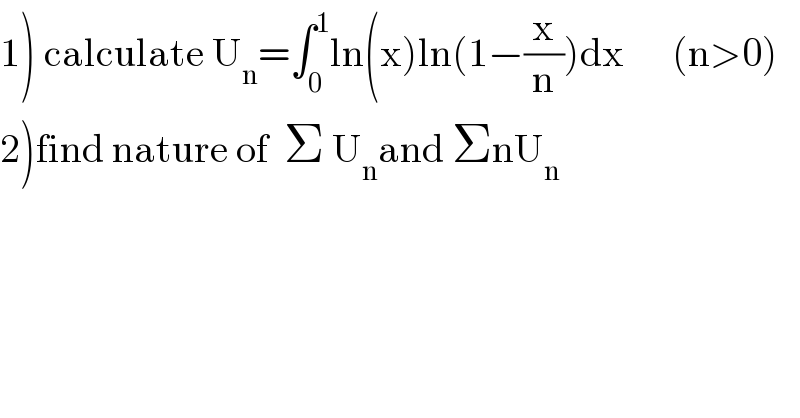
1) calculate U_n =∫_0 ^1 ln(x)ln(1−(x/n))dx (n>0) 2)find nature of Σ U_n and ΣnU_n
$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)\mathrm{dx}\:\:\:\:\:\:\left(\mathrm{n}>\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{find}\:\mathrm{nature}\:\mathrm{of}\:\:\Sigma\:\mathrm{U}_{\mathrm{n}} \mathrm{and}\:\Sigma\mathrm{nU}_{\mathrm{n}} \\ $$
Answered by abdomathmax last updated on 19/May/20
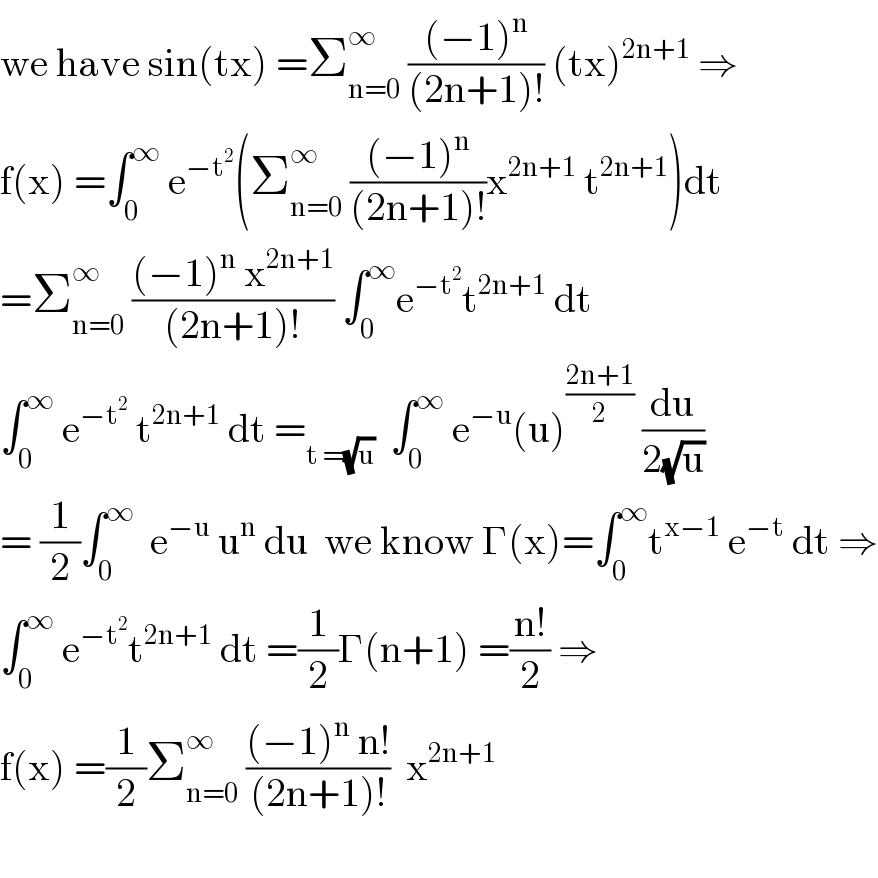
we have sin(tx) =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!)) (tx)^(2n+1) ⇒ f(x) =∫_0 ^∞ e^(−t^2 ) (Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))x^(2n+1) t^(2n+1) )dt =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) ∫_0 ^∞ e^(−t^2 ) t^(2n+1) dt ∫_0 ^∞ e^(−t^2 ) t^(2n+1) dt =_(t =(√u)) ∫_0 ^∞ e^(−u) (u)^((2n+1)/2) (du/(2(√u))) = (1/2)∫_0 ^∞ e^(−u) u^n du we know Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt ⇒ ∫_0 ^∞ e^(−t^2 ) t^(2n+1) dt =(1/2)Γ(n+1) =((n!)/2) ⇒ f(x) =(1/2)Σ_(n=0) ^∞ (((−1)^n n!)/((2n+1)!)) x^(2n+1)
$$\mathrm{we}\:\mathrm{have}\:\mathrm{sin}\left(\mathrm{tx}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\left(\mathrm{tx}\right)^{\mathrm{2n}+\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{t}^{\mathrm{2n}+\mathrm{1}} \right)\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{t}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \:\mathrm{t}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{dt}\:=_{\mathrm{t}\:=\sqrt{\mathrm{u}}} \:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{u}} \left(\mathrm{u}\right)^{\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{u}}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{u}} \:\mathrm{u}^{\mathrm{n}} \:\mathrm{du}\:\:\mathrm{we}\:\mathrm{know}\:\Gamma\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{t}^{\mathrm{2n}+\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\mathrm{n}+\mathrm{1}\right)\:=\frac{\mathrm{n}!}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{n}!}{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\:\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 20/May/20
the Q here is developp at integr serie ∫_0 ^∞ e^(−t^2 ) sin(tx)dt
$$\mathrm{the}\:\mathrm{Q}\:\mathrm{here}\:\mathrm{is}\:\mathrm{developp}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \:\mathrm{sin}\left(\mathrm{tx}\right)\mathrm{dt} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *