Question Number 99578 by mathmax by abdo last updated on 21/Jun/20
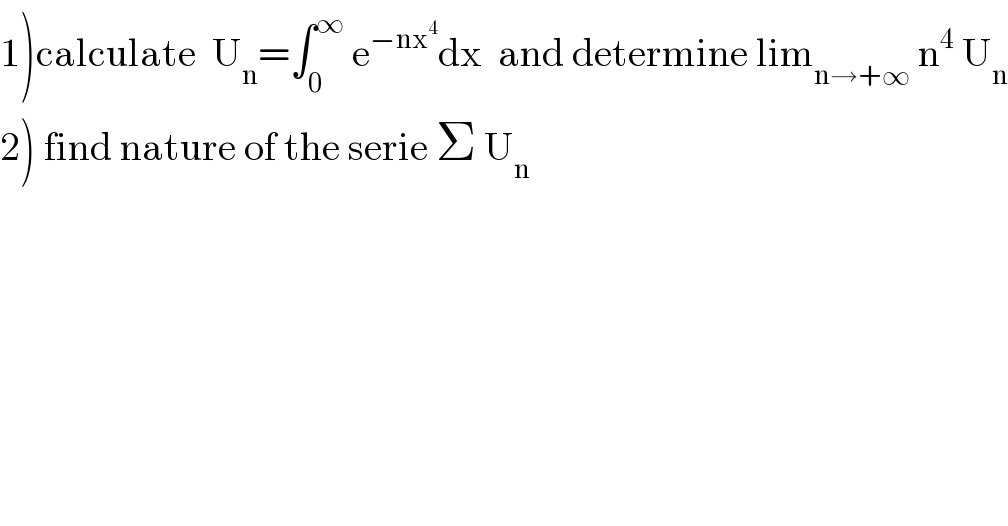
$$\left.\mathrm{1}\right)\mathrm{calculate}\:\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{nx}^{\mathrm{4}} } \mathrm{dx}\:\:\mathrm{and}\:\mathrm{determine}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{n}^{\mathrm{4}} \:\mathrm{U}_{\mathrm{n}} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{the}\:\mathrm{serie}\:\Sigma\:\mathrm{U}_{\mathrm{n}} \\ $$
Answered by maths mind last updated on 22/Jun/20
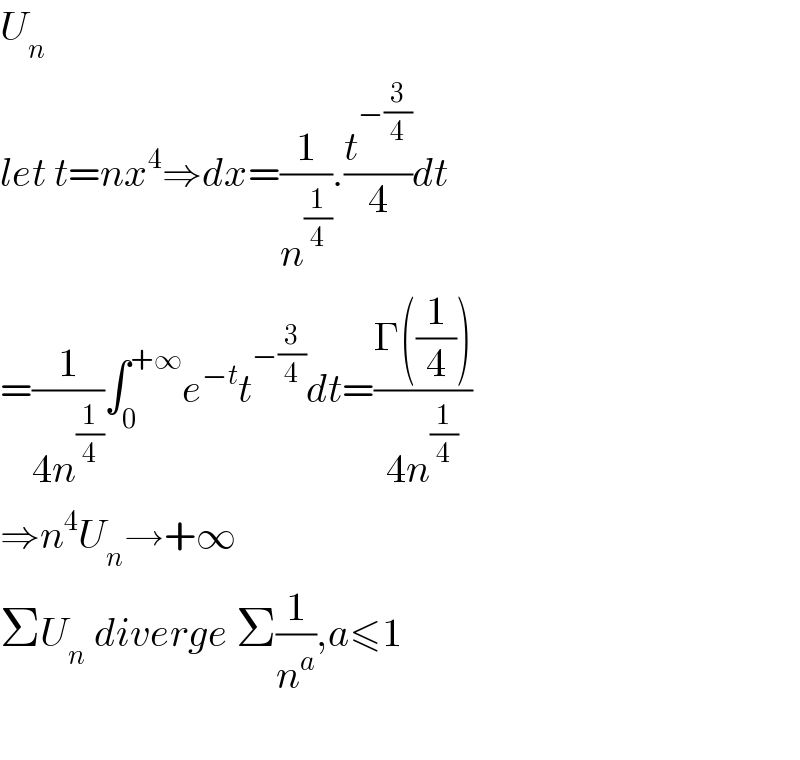
$${U}_{{n}} \\ $$$${let}\:{t}={nx}^{\mathrm{4}} \Rightarrow{dx}=\frac{\mathrm{1}}{{n}^{\frac{\mathrm{1}}{\mathrm{4}}} }.\frac{{t}^{−\frac{\mathrm{3}}{\mathrm{4}}} }{\mathrm{4}}{dt}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{n}^{\frac{\mathrm{1}}{\mathrm{4}}} }\int_{\mathrm{0}} ^{+\infty} {e}^{−{t}} {t}^{−\frac{\mathrm{3}}{\mathrm{4}}} {dt}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}{n}^{\frac{\mathrm{1}}{\mathrm{4}}} } \\ $$$$\Rightarrow{n}^{\mathrm{4}} {U}_{{n}} \rightarrow+\infty \\ $$$$\Sigma{U}_{{n}} \:{diverge}\:\Sigma\frac{\mathrm{1}}{{n}^{{a}} },{a}\leqslant\mathrm{1} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 22/Jun/20
![1) U_n =∫_0 ^∞ e^(−n x^4 ) dx we do the changement nx^4 =t ⇒x^4 =(t/n) ⇒ x =(1/n^(1/4) )t^(1/4) ⇒ U_n =(1/((^4 (√n))))∫_0 ^∞ e^(−t) (1/4) t^((1/4)−1) dt =(1/(4(^4 (√n))))×Γ((1/4)) U_n =(n^(−(1/4)) /4) Γ((1/4)) ⇒n^4 U_n =(n^((15)/4) /4)Γ((1/4))→+∞ (n→∞) 2)Σ_(n=1) ^∞ U_n =(1/4)Γ((1/4))Σ_(n=1) ^∞ (1/n^(1/4) ) and Σ_(n=1) ^∞ (1/n^(1/4) ) have tbe same nature of ∫_1 ^(+∞) (dt/t^(1/4) ) =∫_1 ^(+∞) t^(−(1/4)) dt =[(1/(−(1/4)+1)) t^(−(1/4)+1) ]_0 ^(+∞) =[(4/3) t^(3/4) ]_0 ^∞ =+∞ ⇒ Σ u_n is divergent...](https://www.tinkutara.com/question/Q99642.png)
$$\left.\mathrm{1}\right)\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{n}\:\mathrm{x}^{\mathrm{4}} } \mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{nx}^{\mathrm{4}} \:=\mathrm{t}\:\Rightarrow\mathrm{x}^{\mathrm{4}} \:=\frac{\mathrm{t}}{\mathrm{n}}\:\Rightarrow \\ $$$$\mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{4}}} }\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\Rightarrow\:\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{1}}{\left(^{\mathrm{4}} \sqrt{\mathrm{n}}\right)}\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{4}\left(^{\mathrm{4}} \sqrt{\mathrm{n}}\right)}×\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{n}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{4}}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:\Rightarrow\mathrm{n}^{\mathrm{4}} \:\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{n}^{\frac{\mathrm{15}}{\mathrm{4}}} }{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\rightarrow+\infty\:\left(\mathrm{n}\rightarrow\infty\right) \\ $$$$\left.\mathrm{2}\right)\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{U}_{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{4}}} }\:\:\mathrm{and}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{4}}} }\:\mathrm{have}\:\mathrm{tbe}\:\mathrm{same}\:\mathrm{nature}\:\mathrm{of} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}} }\:=\int_{\mathrm{1}} ^{+\infty} \:\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}}\:\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}} \right]_{\mathrm{0}} ^{+\infty} \:=\left[\frac{\mathrm{4}}{\mathrm{3}}\:\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{4}}} \right]_{\mathrm{0}} ^{\infty} \:=+\infty\:\Rightarrow \\ $$$$\Sigma\:\mathrm{u}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{divergent}… \\ $$
