Question Number 27531 by sirigidiravikumar@gmail.com last updated on 08/Jan/18
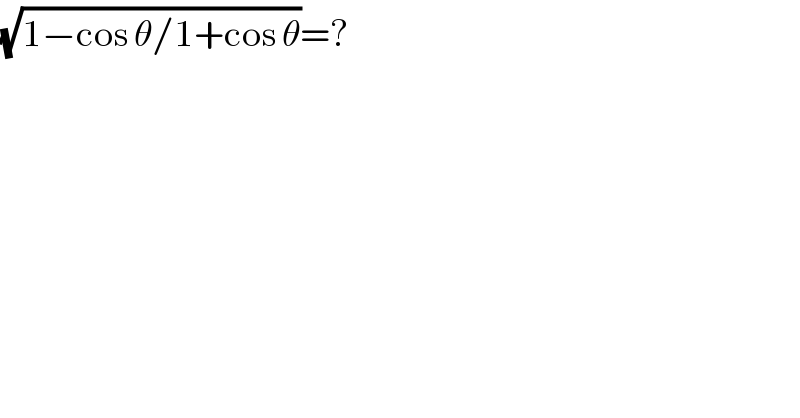
$$\sqrt{\mathrm{1}−\mathrm{cos}\:\theta/\mathrm{1}+\mathrm{cos}\:\theta}=? \\ $$
Commented by Rasheed.Sindhi last updated on 08/Jan/18
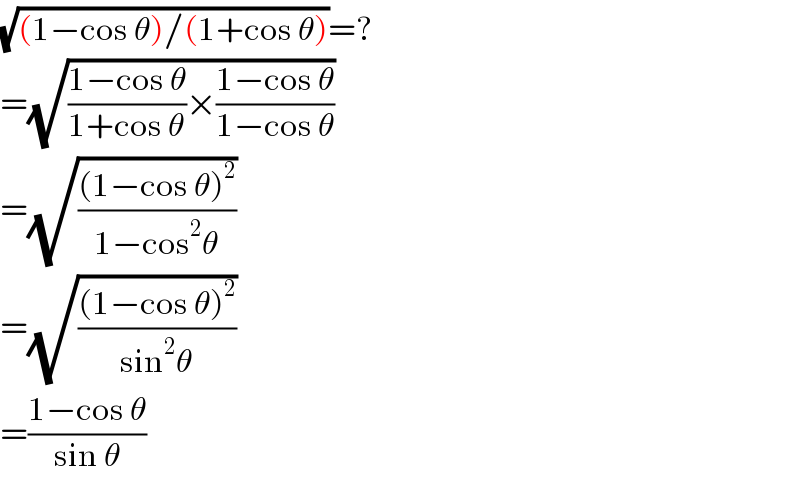
$$\sqrt{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)/\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}=? \\ $$$$=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}×\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}−\mathrm{cos}\:\theta}} \\ $$$$=\sqrt{\frac{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta}} \\ $$$$=\sqrt{\frac{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \theta}} \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta} \\ $$
Commented by sirigidiravikumar@gmail.com last updated on 08/Jan/18
thank you sir
Commented by abdo imad last updated on 08/Jan/18
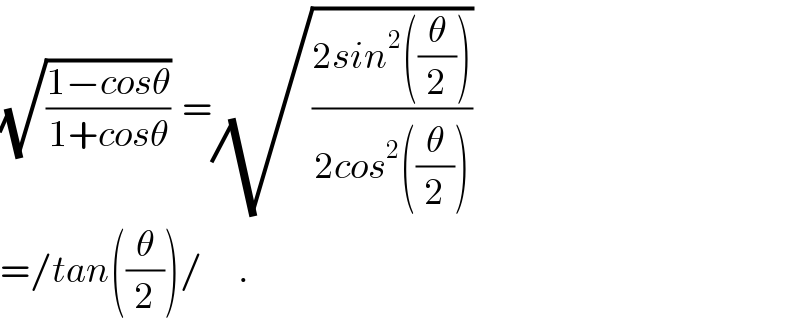
$$\sqrt{\frac{\mathrm{1}−{cos}\theta}{\mathrm{1}+{cos}\theta}}\:\:=\sqrt{\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}} \\ $$$$=/{tan}\left(\frac{\theta}{\mathrm{2}}\right)/\:\:\:\:\:\:. \\ $$
Commented by prakash jain last updated on 08/Jan/18

$$/\mathrm{tan}\:\frac{\theta}{\mathrm{2}}/=\mid\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\mid \\ $$$$\mathrm{Just}\:\mathrm{calrifying}\:\mathrm{since}\:\mathrm{some}\:\mathrm{new} \\ $$$$\mathrm{users}\:\mathrm{may}\:\mathrm{not}\:\mathrm{be}\:\mathrm{aware}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{notation}\:\mathrm{that}\:\mathrm{you}\:\mathrm{are}\:\mathrm{using}. \\ $$
Commented by abdo imad last updated on 08/Jan/18
$${thanks}\:{prakash}… \\ $$
