Question Number 18114 by ibraheem160 last updated on 15/Jul/17
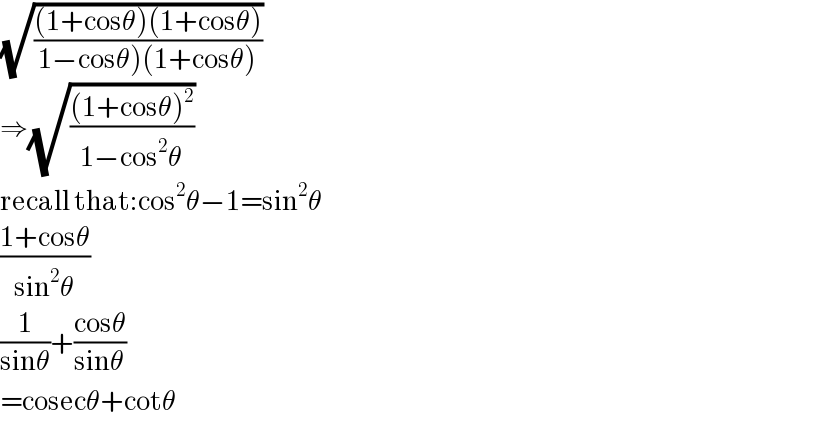
$$\sqrt{\frac{\left(\mathrm{1}+\mathrm{cos}\theta\right)\left(\mathrm{1}+\mathrm{cos}\theta\right)}{\left.\mathrm{1}−\mathrm{cos}\theta\right)\left(\mathrm{1}+\mathrm{cos}\theta\right)}} \\ $$$$\Rightarrow\sqrt{\frac{\left(\mathrm{1}+\mathrm{cos}\theta\right)^{\mathrm{2}} }{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta}} \\ $$$$\mathrm{recall}\:\mathrm{that}:\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{1}=\mathrm{sin}^{\mathrm{2}} \theta \\ $$$$\frac{\mathrm{1}+\mathrm{cos}\theta}{\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\theta}+\frac{\mathrm{cos}\theta}{\mathrm{sin}\theta} \\ $$$$=\mathrm{cosec}\theta+\mathrm{cot}\theta \\ $$
