Question Number 174346 by cortano1 last updated on 30/Jul/22
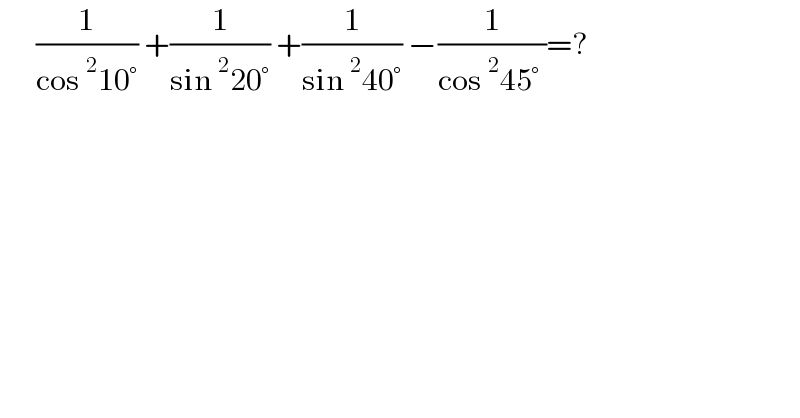
$$\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{10}°}\:+\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{20}°}\:+\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{40}°}\:−\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{45}°\:}=? \\ $$
Answered by behi834171 last updated on 30/Jul/22
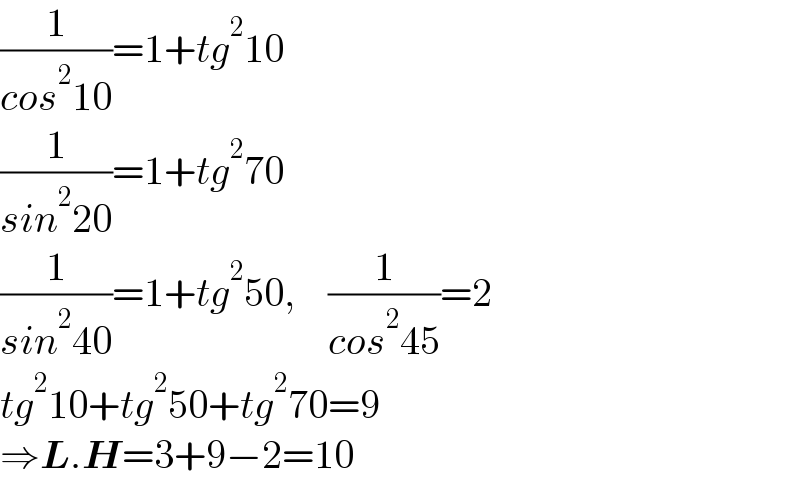
$$\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \mathrm{10}}=\mathrm{1}+{tg}^{\mathrm{2}} \mathrm{10} \\ $$$$\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \mathrm{20}}=\mathrm{1}+{tg}^{\mathrm{2}} \mathrm{70} \\ $$$$\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \mathrm{40}}=\mathrm{1}+{tg}^{\mathrm{2}} \mathrm{50},\:\:\:\:\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \mathrm{45}}=\mathrm{2} \\ $$$${tg}^{\mathrm{2}} \mathrm{10}+{tg}^{\mathrm{2}} \mathrm{50}+{tg}^{\mathrm{2}} \mathrm{70}=\mathrm{9} \\ $$$$\Rightarrow\boldsymbol{{L}}.\boldsymbol{{H}}=\mathrm{3}+\mathrm{9}−\mathrm{2}=\mathrm{10} \\ $$
Commented by cortano1 last updated on 31/Jul/22
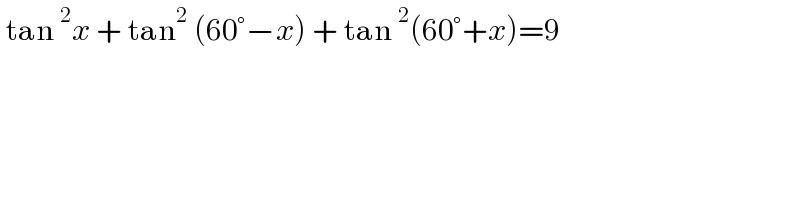
$$\:\mathrm{tan}\:^{\mathrm{2}} {x}\:+\:\mathrm{tan}^{\mathrm{2}} \:\left(\mathrm{60}°−{x}\right)\:+\:\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{60}°+{x}\right)=\mathrm{9} \\ $$
