Question Number 146230 by mathdanisur last updated on 12/Jul/21
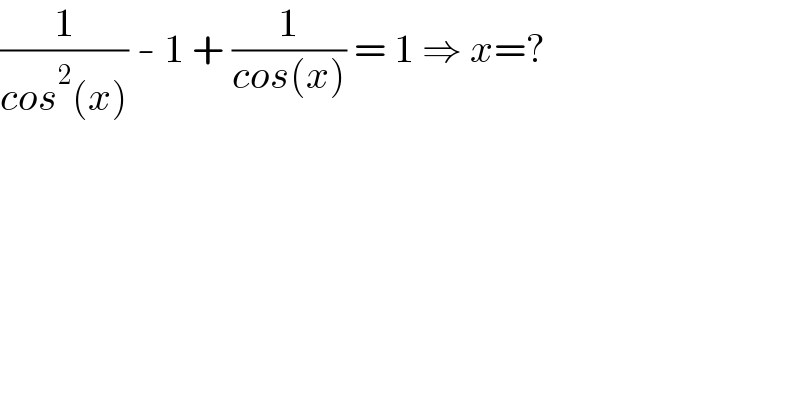
$$\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)}\:-\:\mathrm{1}\:+\:\frac{\mathrm{1}}{{cos}\left({x}\right)}\:=\:\mathrm{1}\:\Rightarrow\:{x}=? \\ $$
Answered by qaz last updated on 12/Jul/21

$$\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\mathrm{1}+\mathrm{sec}\:\mathrm{x}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sec}\:\mathrm{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sec}\:\mathrm{x}=−\mathrm{2}\:\mathrm{or}\:\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{x}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\mathrm{or}\:\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{k}\pi\pm\frac{\pi}{\mathrm{3}}\:\mathrm{or}\:\mathrm{2k}\pi…..\left(\mathrm{k}\in\mathbb{Z}\right) \\ $$
Commented by mathdanisur last updated on 12/Jul/21

$${cool}\:{Ser}\:{thanks} \\ $$
