Menu Close

1-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 163829 by milandou last updated on 11/Jan/22
∫(1/(cos x))
$$\int\frac{\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$
Commented by MJS_new last updated on 11/Jan/22
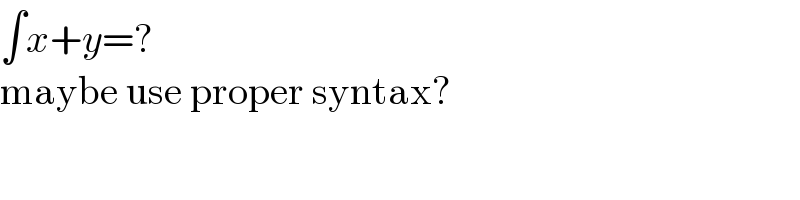
∫x+y=? maybe use proper syntax?
$$\int{x}+{y}=? \\ $$$$\mathrm{maybe}\:\mathrm{use}\:\mathrm{proper}\:\mathrm{syntax}? \\ $$
Answered by Ar Brandon last updated on 11/Jan/22
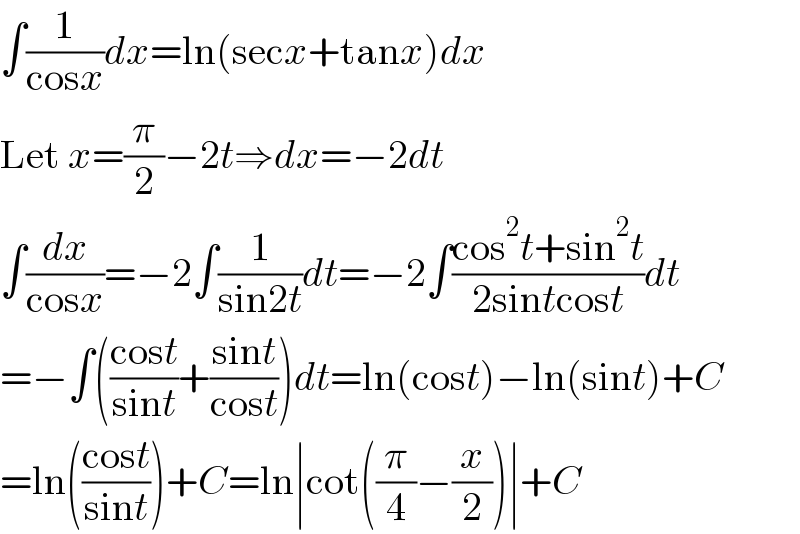
∫(1/(cosx))dx=ln(secx+tanx)dx Let x=(π/2)−2t⇒dx=−2dt ∫(dx/(cosx))=−2∫(1/(sin2t))dt=−2∫((cos^2 t+sin^2 t)/(2sintcost))dt =−∫(((cost)/(sint))+((sint)/(cost)))dt=ln(cost)−ln(sint)+C =ln(((cost)/(sint)))+C=ln∣cot((π/4)−(x/2))∣+C
$$\int\frac{\mathrm{1}}{\mathrm{cos}{x}}{dx}=\mathrm{ln}\left(\mathrm{sec}{x}+\mathrm{tan}{x}\right){dx} \\ $$$$\mathrm{Let}\:{x}=\frac{\pi}{\mathrm{2}}−\mathrm{2}{t}\Rightarrow{dx}=−\mathrm{2}{dt} \\ $$$$\int\frac{{dx}}{\mathrm{cos}{x}}=−\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{sin2}{t}}{dt}=−\mathrm{2}\int\frac{\mathrm{cos}^{\mathrm{2}} {t}+\mathrm{sin}^{\mathrm{2}} {t}}{\mathrm{2sin}{t}\mathrm{cos}{t}}{dt} \\ $$$$=−\int\left(\frac{\mathrm{cos}{t}}{\mathrm{sin}{t}}+\frac{\mathrm{sin}{t}}{\mathrm{cos}{t}}\right){dt}=\mathrm{ln}\left(\mathrm{cos}{t}\right)−\mathrm{ln}\left(\mathrm{sin}{t}\right)+{C} \\ $$$$=\mathrm{ln}\left(\frac{\mathrm{cos}{t}}{\mathrm{sin}{t}}\right)+{C}=\mathrm{ln}\mid\mathrm{cot}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\mid+{C} \\ $$
Answered by Ar Brandon last updated on 11/Jan/22
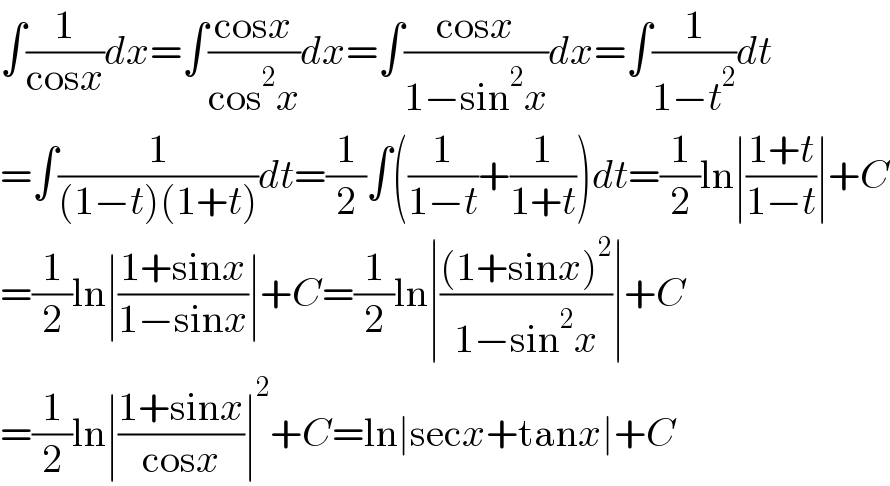
∫(1/(cosx))dx=∫((cosx)/(cos^2 x))dx=∫((cosx)/(1−sin^2 x))dx=∫(1/(1−t^2 ))dt =∫(1/((1−t)(1+t)))dt=(1/2)∫((1/(1−t))+(1/(1+t)))dt=(1/2)ln∣((1+t)/(1−t))∣+C =(1/2)ln∣((1+sinx)/(1−sinx))∣+C=(1/2)ln∣(((1+sinx)^2 )/(1−sin^2 x))∣+C =(1/2)ln∣((1+sinx)/(cosx))∣^2 +C=ln∣secx+tanx∣+C
$$\int\frac{\mathrm{1}}{\mathrm{cos}{x}}{dx}=\int\frac{\mathrm{cos}{x}}{\mathrm{cos}^{\mathrm{2}} {x}}{dx}=\int\frac{\mathrm{cos}{x}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}}{dx}=\int\frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$=\int\frac{\mathrm{1}}{\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{sin}{x}}{\mathrm{1}−\mathrm{sin}{x}}\mid+{C}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\left(\mathrm{1}+\mathrm{sin}{x}\right)^{\mathrm{2}} }{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{sin}{x}}{\mathrm{cos}{x}}\mid^{\mathrm{2}} +{C}=\mathrm{ln}\mid\mathrm{sec}{x}+\mathrm{tan}{x}\mid+{C} \\ $$
Answered by stelor last updated on 12/Jan/22
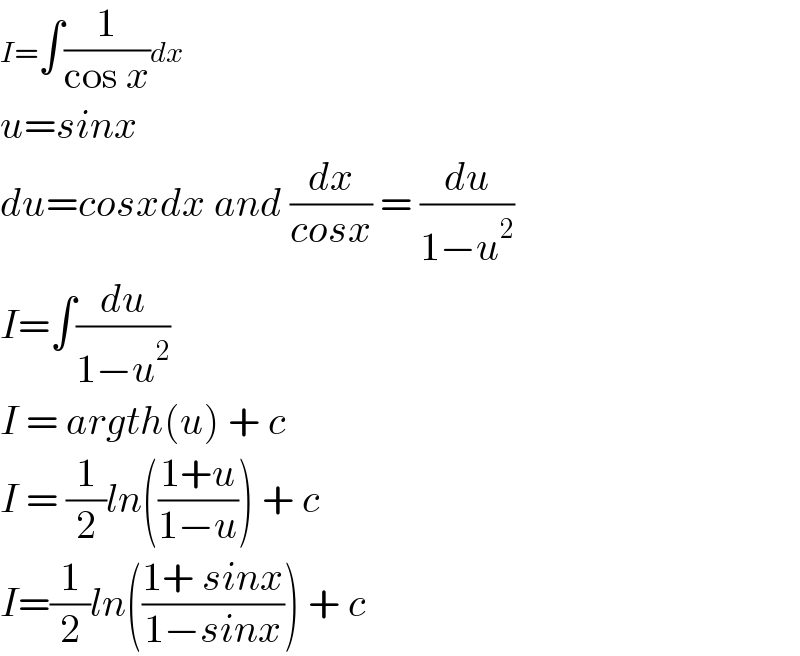
I=∫(1/(cos x))dx u=sinx du=cosxdx and (dx/(cosx)) = (du/(1−u^2 )) I=∫(du/(1−u^2 )) I = argth(u) + c I = (1/2)ln(((1+u)/(1−u))) + c I=(1/2)ln(((1+ sinx)/(1−sinx))) + c
$${I}=\int\frac{\mathrm{1}}{\mathrm{cos}\:{x}}{dx} \\ $$$${u}={sinx} \\ $$$${du}={cosxdx}\:{and}\:\frac{{dx}}{{cosx}}\:=\:\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$${I}=\int\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$${I}\:=\:{argth}\left({u}\right)\:+\:{c} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\right)\:+\:{c} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+\:{sinx}}{\mathrm{1}−{sinx}}\right)\:+\:{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *