Question Number 106295 by bobhans last updated on 04/Aug/20
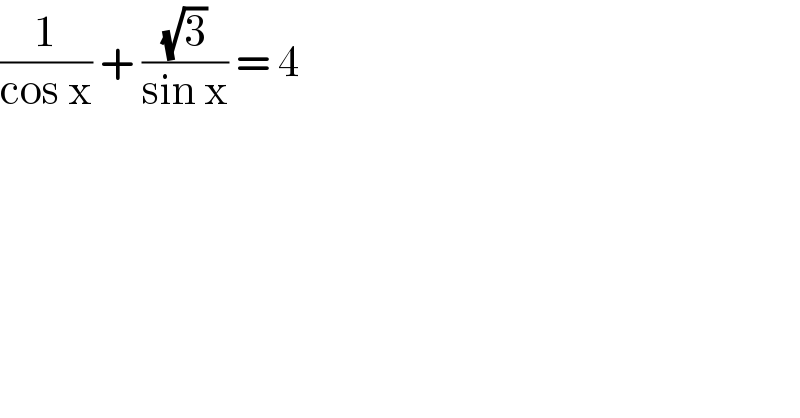
$$\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}}\:+\:\frac{\sqrt{\mathrm{3}}}{\mathrm{sin}\:\mathrm{x}}\:=\:\mathrm{4}\: \\ $$
Answered by bemath last updated on 04/Aug/20
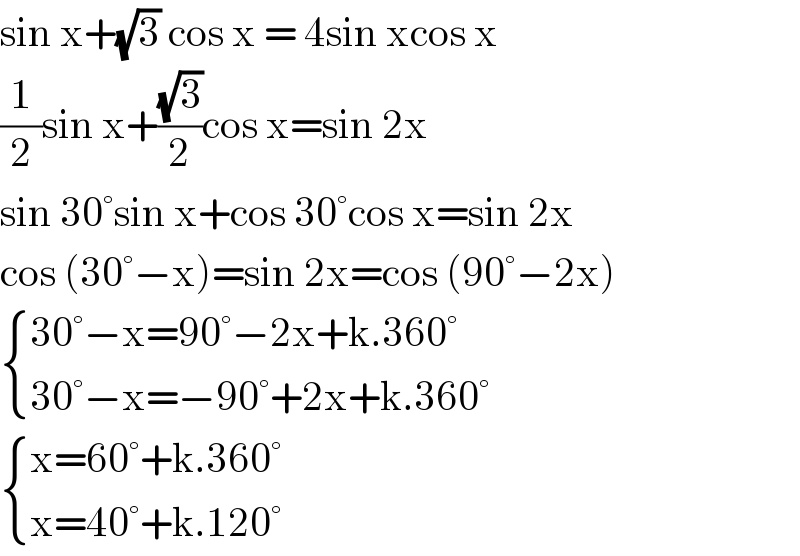
$$\mathrm{sin}\:\mathrm{x}+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{4sin}\:\mathrm{xcos}\:\mathrm{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\mathrm{x}=\mathrm{sin}\:\mathrm{2x} \\ $$$$\mathrm{sin}\:\mathrm{30}°\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{30}°\mathrm{cos}\:\mathrm{x}=\mathrm{sin}\:\mathrm{2x} \\ $$$$\mathrm{cos}\:\left(\mathrm{30}°−\mathrm{x}\right)=\mathrm{sin}\:\mathrm{2x}=\mathrm{cos}\:\left(\mathrm{90}°−\mathrm{2x}\right) \\ $$$$\begin{cases}{\mathrm{30}°−\mathrm{x}=\mathrm{90}°−\mathrm{2x}+\mathrm{k}.\mathrm{360}°}\\{\mathrm{30}°−\mathrm{x}=−\mathrm{90}°+\mathrm{2x}+\mathrm{k}.\mathrm{360}°}\end{cases} \\ $$$$\begin{cases}{\mathrm{x}=\mathrm{60}°+\mathrm{k}.\mathrm{360}°}\\{\mathrm{x}=\mathrm{40}°+\mathrm{k}.\mathrm{120}°}\end{cases} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Aug/20
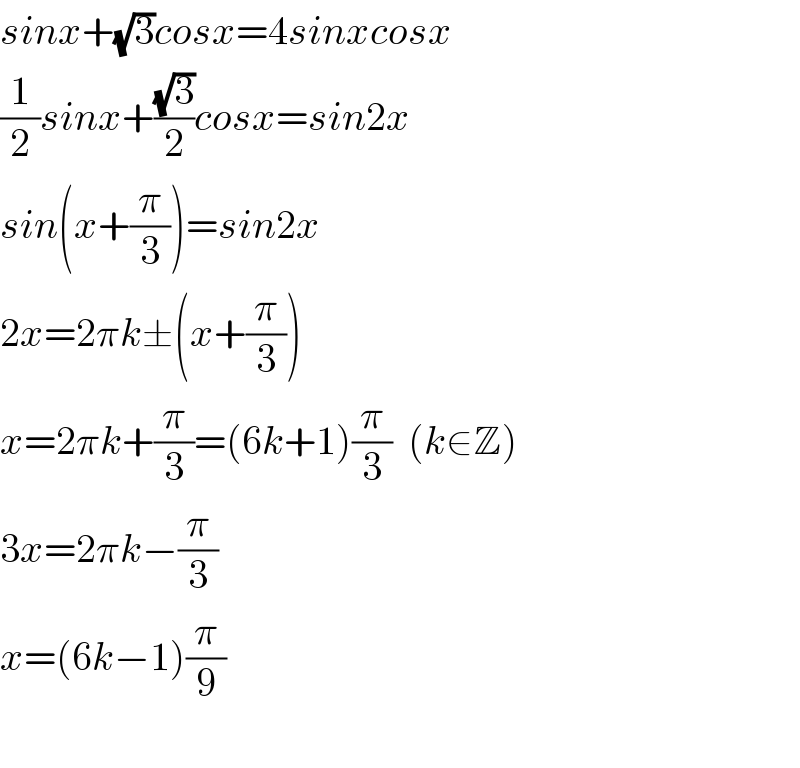
$${sinx}+\sqrt{\mathrm{3}}{cosx}=\mathrm{4}{sinxcosx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{sinx}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cosx}={sin}\mathrm{2}{x} \\ $$$${sin}\left({x}+\frac{\pi}{\mathrm{3}}\right)={sin}\mathrm{2}{x} \\ $$$$\mathrm{2}{x}=\mathrm{2}\pi{k}\pm\left({x}+\frac{\pi}{\mathrm{3}}\right) \\ $$$${x}=\mathrm{2}\pi{k}+\frac{\pi}{\mathrm{3}}=\left(\mathrm{6}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{3}}\:\:\left({k}\in\mathbb{Z}\right) \\ $$$$\mathrm{3}{x}=\mathrm{2}\pi{k}−\frac{\pi}{\mathrm{3}} \\ $$$${x}=\left(\mathrm{6}{k}−\mathrm{1}\right)\frac{\pi}{\mathrm{9}} \\ $$$$ \\ $$
