Menu Close

1-cosz-z-1-2-dz-z-1-2-cosz-z-1-2-dz-z-1-

Tinku Tara 0 Comments
Pin




Question Number 147213 by Mrsof last updated on 18/Jul/21
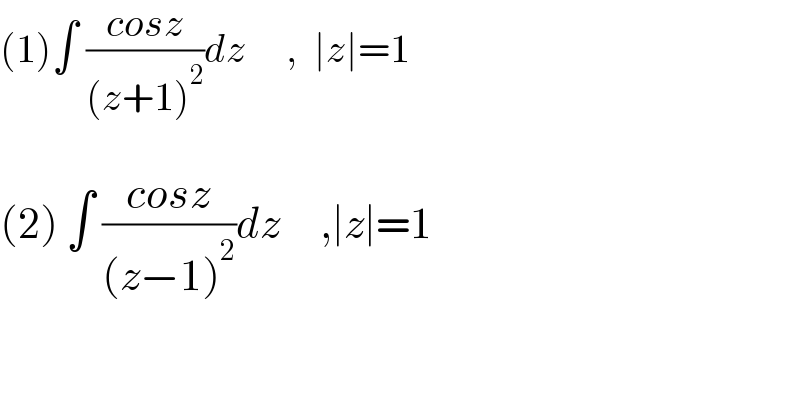
(1)∫ ((cosz)/((z+1)^2 ))dz , ∣z∣=1 (2) ∫ ((cosz)/((z−1)^2 ))dz ,∣z∣=1
$$\left(\mathrm{1}\right)\int\:\frac{{cosz}}{\left({z}+\mathrm{1}\right)^{\mathrm{2}} }{dz}\:\:\:\:\:,\:\:\mid{z}\mid=\mathrm{1} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\int\:\frac{{cosz}}{\left({z}−\mathrm{1}\right)^{\mathrm{2}} }{dz}\:\:\:\:\:,\mid{z}\mid=\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 19/Jul/21
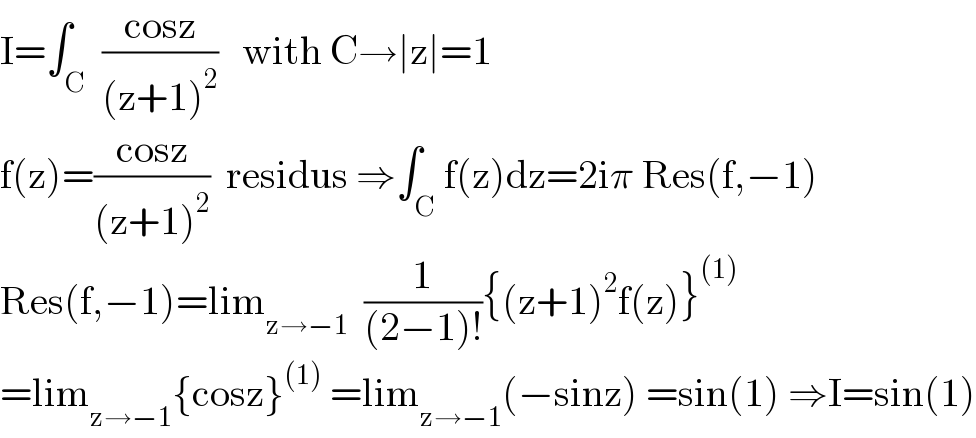
I=∫_C ((cosz)/((z+1)^2 )) with C→∣z∣=1 f(z)=((cosz)/((z+1)^2 )) residus ⇒∫_C f(z)dz=2iπ Res(f,−1) Res(f,−1)=lim_(z→−1) (1/((2−1)!)){(z+1)^2 f(z)}^((1)) =lim_(z→−1) {cosz}^((1)) =lim_(z→−1) (−sinz) =sin(1) ⇒I=sin(1)
$$\mathrm{I}=\int_{\mathrm{C}} \:\frac{\mathrm{cosz}}{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:\mathrm{with}\:\mathrm{C}\rightarrow\mid\mathrm{z}\mid=\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{cosz}}{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\mathrm{residus}\:\Rightarrow\int_{\mathrm{C}} \mathrm{f}\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},−\mathrm{1}\right) \\ $$$$\mathrm{Res}\left(\mathrm{f},−\mathrm{1}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{f}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\mathrm{cosz}\right\}^{\left(\mathrm{1}\right)} \:=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left(−\mathrm{sinz}\right)\:=\mathrm{sin}\left(\mathrm{1}\right)\:\Rightarrow\mathrm{I}=\mathrm{sin}\left(\mathrm{1}\right) \\ $$
Answered by mathmax by abdo last updated on 19/Jul/21
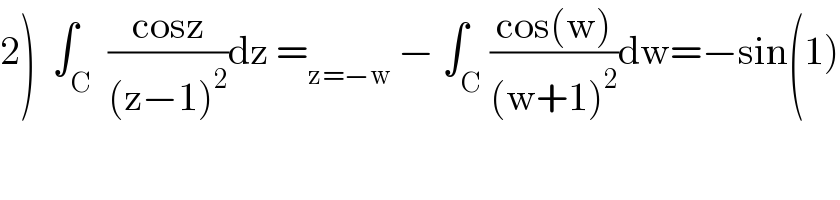
2) ∫_C ((cosz)/((z−1)^2 ))dz =_(z=−w) − ∫_C ((cos(w))/((w+1)^2 ))dw=−sin(1)
$$\left.\mathrm{2}\right)\:\:\int_{\mathrm{C}} \:\frac{\mathrm{cosz}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dz}\:=_{\mathrm{z}=−\mathrm{w}} \:−\:\int_{\mathrm{C}} \frac{\mathrm{cos}\left(\mathrm{w}\right)}{\left(\mathrm{w}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dw}=−\mathrm{sin}\left(\mathrm{1}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *