Menu Close

1-d-1-sin-2-2-2-d-1-cos-2-2-3-d-1-sin-2-1-cos-2-

Tinku Tara 0 Comments
Pin




Question Number 36738 by MJS last updated on 04/Jun/18
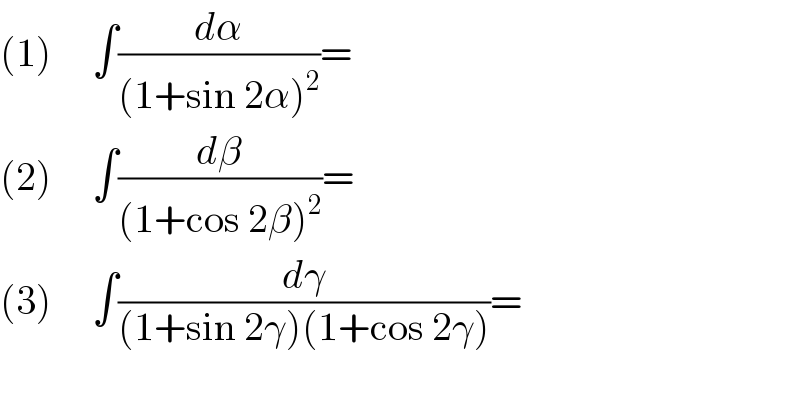
(1) ∫(dα/((1+sin 2α)^2 ))= (2) ∫(dβ/((1+cos 2β)^2 ))= (3) ∫(dγ/((1+sin 2γ)(1+cos 2γ)))=
$$\left(\mathrm{1}\right)\:\:\:\:\:\int\frac{{d}\alpha}{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}\alpha\right)^{\mathrm{2}} }= \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\int\frac{{d}\beta}{\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\beta\right)^{\mathrm{2}} }= \\ $$$$\left(\mathrm{3}\right)\:\:\:\:\:\int\frac{{d}\gamma}{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}\gamma\right)\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\gamma\right)}= \\ $$
Commented by behi83417@gmail.com last updated on 05/Jun/18
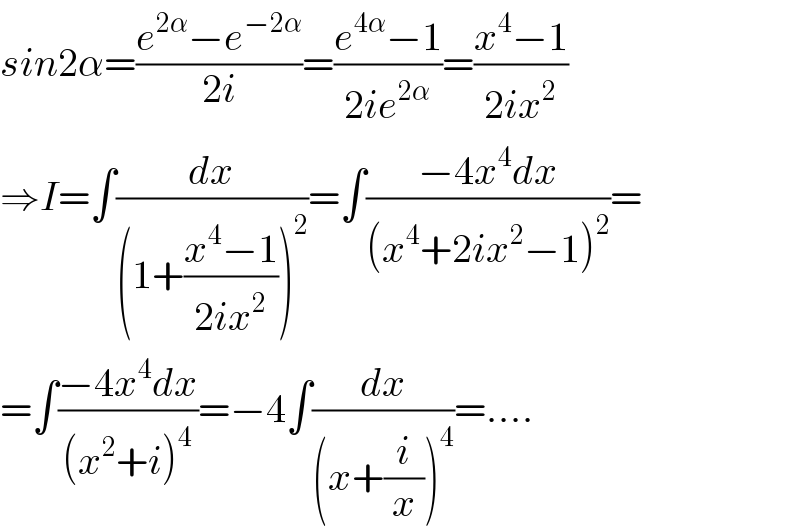
sin2α=((e^(2α) −e^(−2α) )/(2i))=((e^(4α) −1)/(2ie^(2α) ))=((x^4 −1)/(2ix^2 )) ⇒I=∫(dx/((1+((x^4 −1)/(2ix^2 )))^2 ))=∫((−4x^4 dx)/((x^4 +2ix^2 −1)^2 ))= =∫((−4x^4 dx)/((x^2 +i)^4 ))=−4∫(dx/((x+(i/x))^4 ))=....
$${sin}\mathrm{2}\alpha=\frac{{e}^{\mathrm{2}\alpha} −{e}^{−\mathrm{2}\alpha} }{\mathrm{2}{i}}=\frac{{e}^{\mathrm{4}\alpha} −\mathrm{1}}{\mathrm{2}{ie}^{\mathrm{2}\alpha} }=\frac{{x}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}{ix}^{\mathrm{2}} } \\ $$$$\Rightarrow{I}=\int\frac{{dx}}{\left(\mathrm{1}+\frac{{x}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}{ix}^{\mathrm{2}} }\right)^{\mathrm{2}} }=\int\frac{−\mathrm{4}{x}^{\mathrm{4}} {dx}}{\left({x}^{\mathrm{4}} +\mathrm{2}{ix}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\int\frac{−\mathrm{4}{x}^{\mathrm{4}} {dx}}{\left({x}^{\mathrm{2}} +{i}\right)^{\mathrm{4}} }=−\mathrm{4}\int\frac{{dx}}{\left({x}+\frac{{i}}{{x}}\right)^{\mathrm{4}} }=…. \\ $$
Commented by abdo.msup.com last updated on 05/Jun/18
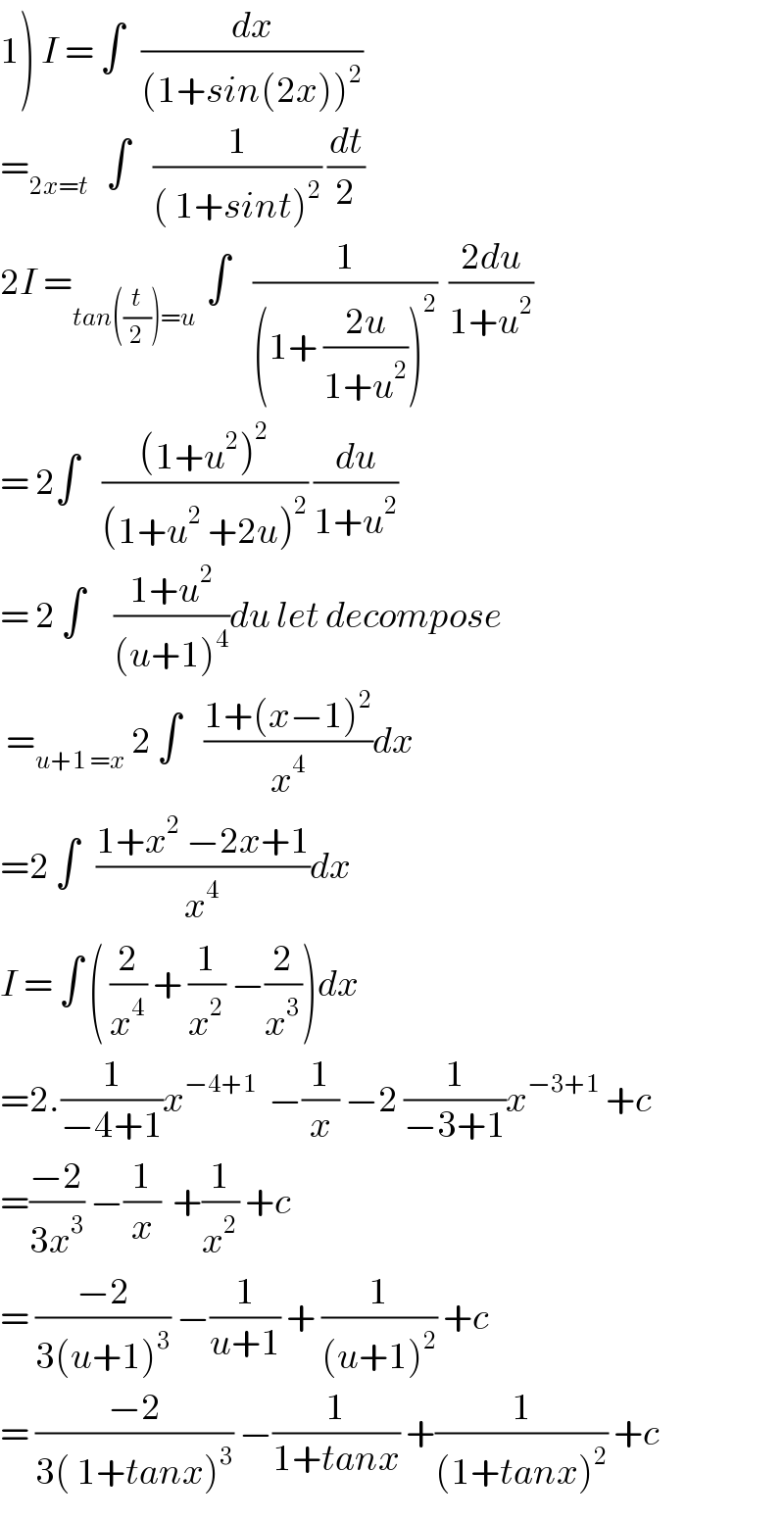
1) I = ∫ (dx/((1+sin(2x))^2 )) =_(2x=t) ∫ (1/(( 1+sint)^2 )) (dt/2) 2I =_(tan((t/2))=u ) ∫ (1/((1+ ((2u)/(1+u^2 )))^2 )) ((2du)/(1+u^2 )) = 2∫ (((1+u^2 )^2 )/((1+u^2 +2u)^2 )) (du/(1+u^2 )) = 2 ∫ ((1+u^2 )/((u+1)^4 ))du let decompose =_(u+1 =x) 2 ∫ ((1+(x−1)^2 )/x^4 )dx =2 ∫ ((1+x^2 −2x+1)/x^4 )dx I = ∫ ( (2/x^4 ) + (1/x^2 ) −(2/x^3 ))dx =2.(1/(−4+1))x^(−4+1) −(1/x) −2 (1/(−3+1))x^(−3+1) +c =((−2)/(3x^3 )) −(1/x) +(1/x^2 ) +c = ((−2)/(3(u+1)^3 )) −(1/(u+1)) + (1/((u+1)^2 )) +c = ((−2)/(3( 1+tanx)^3 )) −(1/(1+tanx)) +(1/((1+tanx)^2 )) +c
$$\left.\mathrm{1}\right)\:{I}\:=\:\int\:\:\:\frac{{dx}}{\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} } \\ $$$$=_{\mathrm{2}{x}={t}} \:\:\:\int\:\:\:\:\frac{\mathrm{1}}{\left(\:\mathrm{1}+{sint}\right)^{\mathrm{2}} }\:\frac{{dt}}{\mathrm{2}} \\ $$$$\mathrm{2}{I}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:} \:\int\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\int\:\:\:\:\frac{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{u}\right)^{\mathrm{2}} }\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\:\int\:\:\:\:\:\frac{\mathrm{1}+{u}^{\mathrm{2}} }{\left({u}+\mathrm{1}\right)^{\mathrm{4}} }{du}\:{let}\:{decompose} \\ $$$$\:=_{{u}+\mathrm{1}\:={x}} \:\mathrm{2}\:\int\:\:\:\:\frac{\mathrm{1}+\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{4}} }{dx} \\ $$$$=\mathrm{2}\:\int\:\:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} \:−\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{4}} }{dx} \\ $$$${I}\:=\:\int\:\left(\:\frac{\mathrm{2}}{{x}^{\mathrm{4}} }\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\right){dx} \\ $$$$=\mathrm{2}.\frac{\mathrm{1}}{−\mathrm{4}+\mathrm{1}}{x}^{−\mathrm{4}+\mathrm{1}} \:\:−\frac{\mathrm{1}}{{x}}\:−\mathrm{2}\:\frac{\mathrm{1}}{−\mathrm{3}+\mathrm{1}}{x}^{−\mathrm{3}+\mathrm{1}} \:+{c} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{3}{x}^{\mathrm{3}} }\:−\frac{\mathrm{1}}{{x}}\:\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+{c} \\ $$$$=\:\frac{−\mathrm{2}}{\mathrm{3}\left({u}+\mathrm{1}\right)^{\mathrm{3}} }\:−\frac{\mathrm{1}}{{u}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:+{c} \\ $$$$=\:\frac{−\mathrm{2}}{\mathrm{3}\left(\:\mathrm{1}+{tanx}\right)^{\mathrm{3}} }\:−\frac{\mathrm{1}}{\mathrm{1}+{tanx}}\:+\frac{\mathrm{1}}{\left(\mathrm{1}+{tanx}\right)^{\mathrm{2}} }\:+{c} \\ $$
Commented by abdo.msup.com last updated on 05/Jun/18
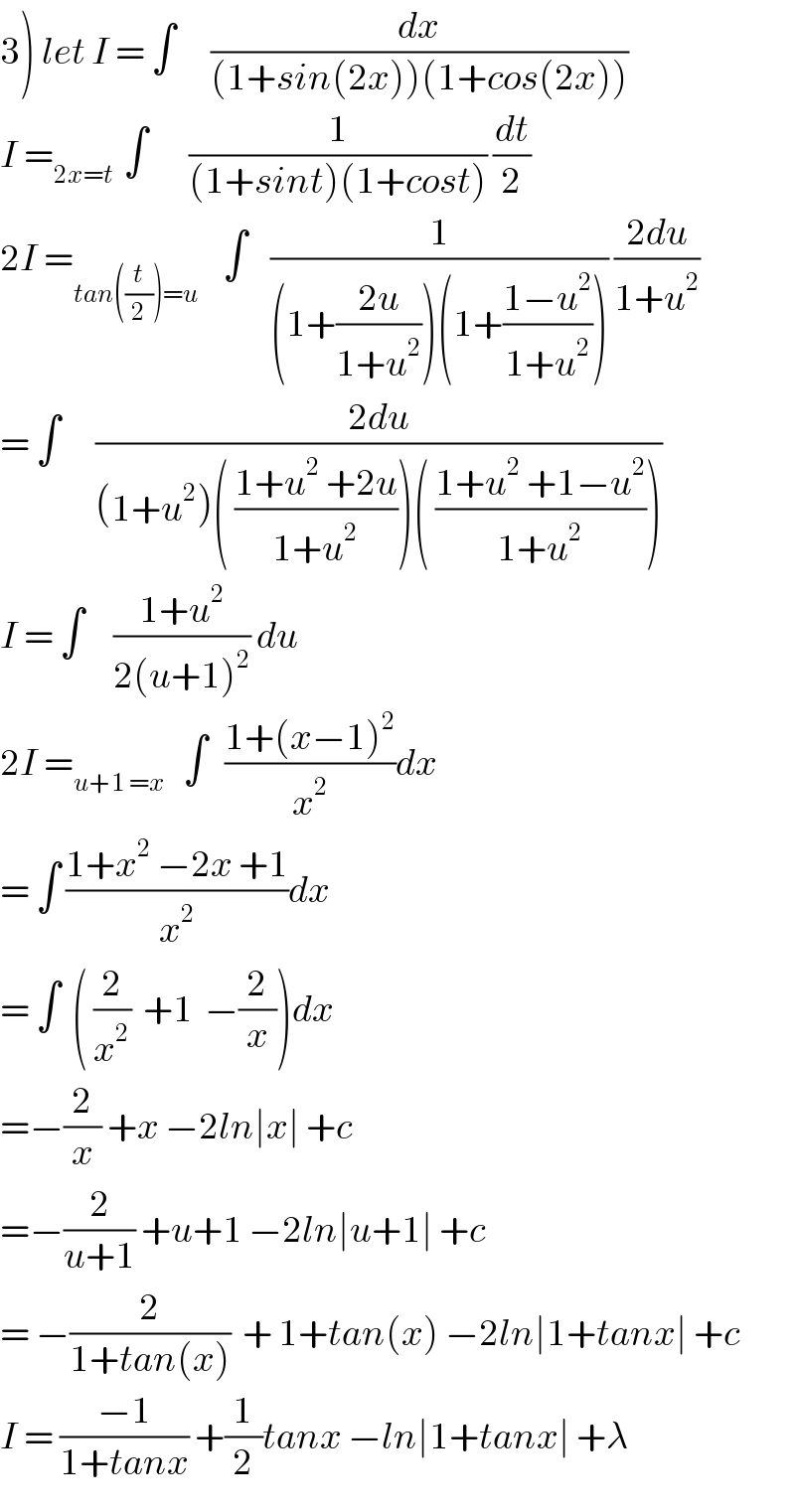
3) let I = ∫ (dx/((1+sin(2x))(1+cos(2x)))) I =_(2x=t ) ∫ (1/((1+sint)(1+cost))) (dt/2) 2I =_(tan((t/2))=u) ∫ (1/((1+((2u)/(1+u^2 )))(1+((1−u^2 )/(1+u^2 ))))) ((2du)/(1+u^2 )) = ∫ ((2du)/((1+u^2 )( ((1+u^2 +2u)/(1+u^2 )))( ((1+u^2 +1−u^2 )/(1+u^2 ))))) I = ∫ ((1+u^2 )/(2(u+1)^2 )) du 2I =_(u+1 =x) ∫ ((1+(x−1)^2 )/x^2 )dx = ∫ ((1+x^2 −2x +1)/x^2 )dx = ∫ ( (2/x^2 ) +1 −(2/x))dx =−(2/x) +x −2ln∣x∣ +c =−(2/(u+1)) +u+1 −2ln∣u+1∣ +c = −(2/(1+tan(x))) + 1+tan(x) −2ln∣1+tanx∣ +c I = ((−1)/(1+tanx)) +(1/2)tanx −ln∣1+tanx∣ +λ
$$\left.\mathrm{3}\right)\:{let}\:{I}\:=\:\int\:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\right)\left(\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)\right)} \\ $$$${I}\:=_{\mathrm{2}{x}={t}\:} \:\int\:\:\:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{sint}\right)\left(\mathrm{1}+{cost}\right)}\:\frac{{dt}}{\mathrm{2}} \\ $$$$\mathrm{2}{I}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\:\int\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\:\frac{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)\left(\:\frac{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)} \\ $$$${I}\:=\:\int\:\:\:\:\:\frac{\mathrm{1}+{u}^{\mathrm{2}} }{\mathrm{2}\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:{du} \\ $$$$\mathrm{2}{I}\:=_{{u}+\mathrm{1}\:={x}} \:\:\:\int\:\:\:\frac{\mathrm{1}+\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }{dx} \\ $$$$=\:\int\:\frac{\mathrm{1}+{x}^{\mathrm{2}} \:−\mathrm{2}{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$=\:\int\:\:\left(\:\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\:\:+\mathrm{1}\:\:−\frac{\mathrm{2}}{{x}}\right){dx} \\ $$$$=−\frac{\mathrm{2}}{{x}}\:+{x}\:−\mathrm{2}{ln}\mid{x}\mid\:+{c} \\ $$$$=−\frac{\mathrm{2}}{{u}+\mathrm{1}}\:+{u}+\mathrm{1}\:−\mathrm{2}{ln}\mid{u}+\mathrm{1}\mid\:+{c} \\ $$$$=\:−\frac{\mathrm{2}}{\mathrm{1}+{tan}\left({x}\right)}\:\:+\:\mathrm{1}+{tan}\left({x}\right)\:−\mathrm{2}{ln}\mid\mathrm{1}+{tanx}\mid\:+{c} \\ $$$${I}\:=\:\frac{−\mathrm{1}}{\mathrm{1}+{tanx}}\:+\frac{\mathrm{1}}{\mathrm{2}}{tanx}\:−{ln}\mid\mathrm{1}+{tanx}\mid\:+\lambda \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
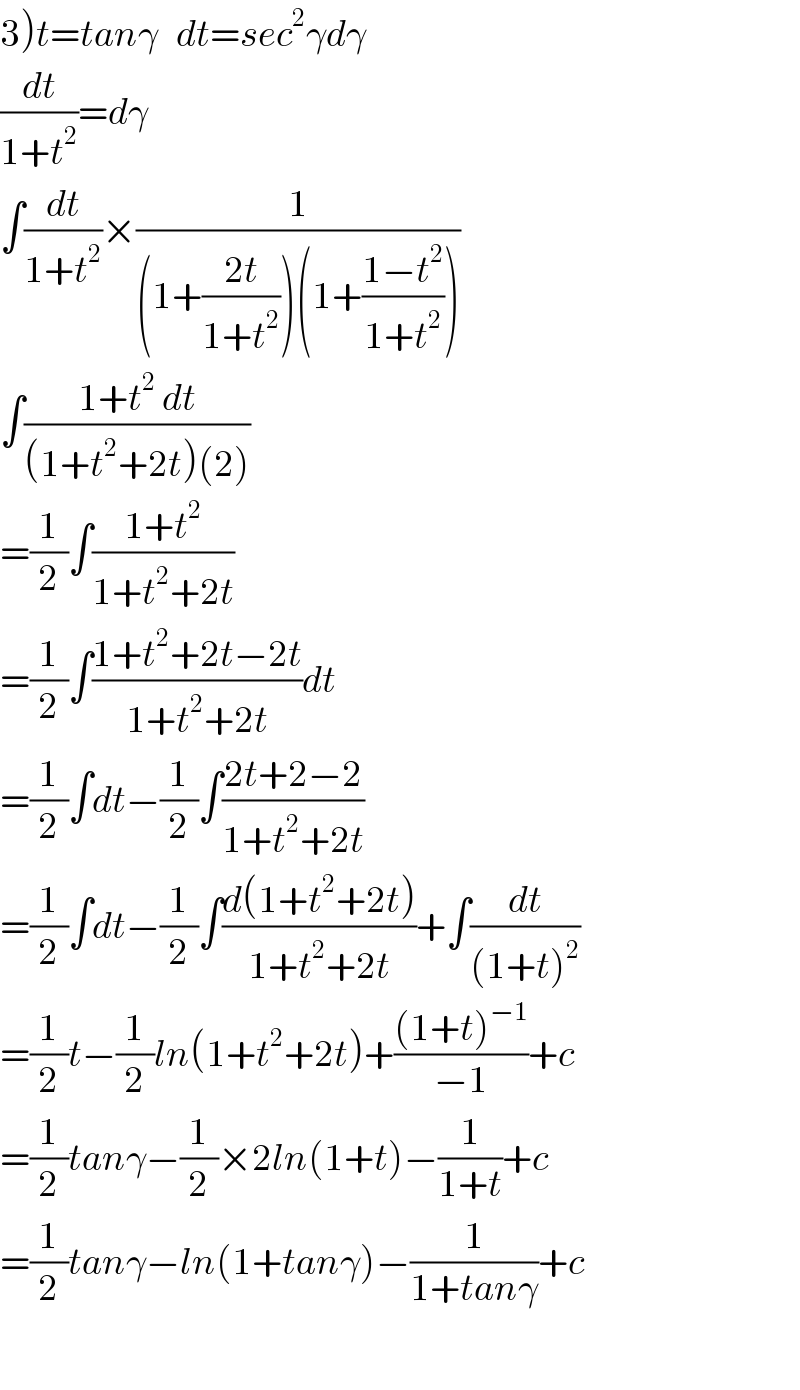
3)t=tanγ dt=sec^2 γdγ (dt/(1+t^2 ))=dγ ∫(dt/(1+t^2 ))×(1/((1+((2t)/(1+t^2 )))(1+((1−t^2 )/(1+t^2 ))))) ∫((1+t^2 dt)/((1+t^2 +2t)(2))) =(1/2)∫((1+t^2 )/(1+t^2 +2t)) =(1/2)∫((1+t^2 +2t−2t)/(1+t^2 +2t))dt =(1/2)∫dt−(1/2)∫((2t+2−2)/(1+t^2 +2t)) =(1/2)∫dt−(1/2)∫((d(1+t^2 +2t))/(1+t^2 +2t))+∫(dt/((1+t)^2 )) =(1/2)t−(1/2)ln(1+t^2 +2t)+(((1+t)^(−1) )/(−1))+c =(1/2)tanγ−(1/2)×2ln(1+t)−(1/(1+t))+c =(1/2)tanγ−ln(1+tanγ)−(1/(1+tanγ))+c
$$\left.\mathrm{3}\right){t}={tan}\gamma\:\:\:{dt}={sec}^{\mathrm{2}} \gamma{d}\gamma \\ $$$$\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }={d}\gamma \\ $$$$\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$\int\frac{\mathrm{1}+{t}^{\mathrm{2}} \:{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{t}+\mathrm{2}−\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}}+\int\frac{{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{t}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)+\frac{\left(\mathrm{1}+{t}\right)^{−\mathrm{1}} }{−\mathrm{1}}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{tan}\gamma−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}{ln}\left(\mathrm{1}+{t}\right)−\frac{\mathrm{1}}{\mathrm{1}+{t}}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{tan}\gamma−{ln}\left(\mathrm{1}+{tan}\gamma\right)−\frac{\mathrm{1}}{\mathrm{1}+{tan}\gamma}+{c} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
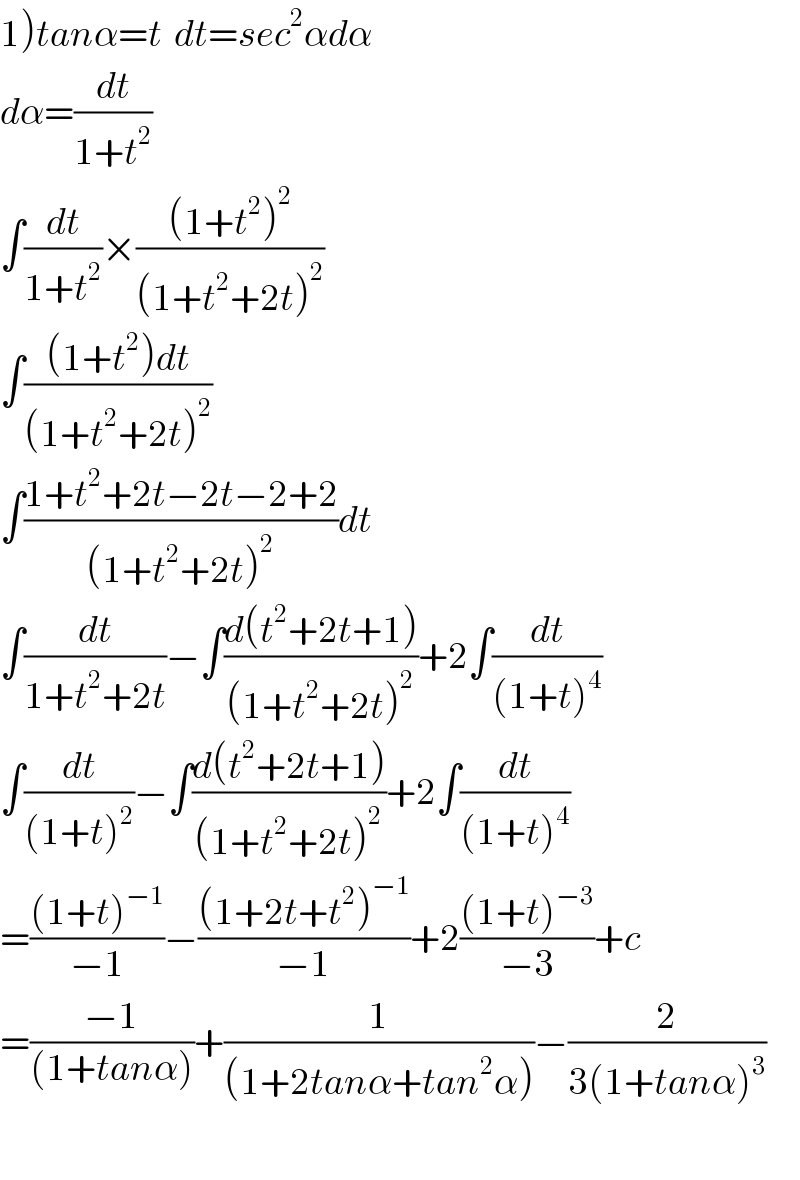
1)tanα=t dt=sec^2 αdα dα=(dt/(1+t^2 )) ∫(dt/(1+t^2 ))×(((1+t^2 )^2 )/((1+t^2 +2t)^2 )) ∫(((1+t^2 )dt)/((1+t^2 +2t)^2 )) ∫((1+t^2 +2t−2t−2+2)/((1+t^2 +2t)^2 ))dt ∫(dt/(1+t^2 +2t))−∫((d(t^2 +2t+1))/((1+t^2 +2t)^2 ))+2∫(dt/((1+t)^4 )) ∫(dt/((1+t)^2 ))−∫((d(t^2 +2t+1))/((1+t^2 +2t)^2 ))+2∫(dt/((1+t)^4 )) =(((1+t)^(−1) )/(−1))−(((1+2t+t^2 )^(−1) )/(−1))+2(((1+t)^(−3) )/(−3))+c =((−1)/((1+tanα)))+(1/((1+2tanα+tan^2 α)))−(2/(3(1+tanα)^3 ))
$$\left.\mathrm{1}\right){tan}\alpha={t}\:\:{dt}={sec}^{\mathrm{2}} \alpha{d}\alpha \\ $$$${d}\alpha=\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)^{\mathrm{2}} } \\ $$$$\int\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{2}{t}−\mathrm{2}+\mathrm{2}}{\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)^{\mathrm{2}} }{dt} \\ $$$$\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}}−\int\frac{{d}\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)^{\mathrm{2}} }+\mathrm{2}\int\frac{{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{4}} } \\ $$$$\int\frac{{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }−\int\frac{{d}\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)^{\mathrm{2}} }+\mathrm{2}\int\frac{{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{4}} } \\ $$$$=\frac{\left(\mathrm{1}+{t}\right)^{−\mathrm{1}} }{−\mathrm{1}}−\frac{\left(\mathrm{1}+\mathrm{2}{t}+{t}^{\mathrm{2}} \right)^{−\mathrm{1}} }{−\mathrm{1}}+\mathrm{2}\frac{\left(\mathrm{1}+{t}\right)^{−\mathrm{3}} }{−\mathrm{3}}+{c} \\ $$$$=\frac{−\mathrm{1}}{\left(\mathrm{1}+{tan}\alpha\right)}+\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2}{tan}\alpha+{tan}^{\mathrm{2}} \alpha\right)}−\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{1}+{tan}\alpha\right)^{\mathrm{3}} } \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *