Question Number 104509 by bobhans last updated on 22/Jul/20

$$\left(\mathrm{1}\right)\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:−\mathrm{7}\:\frac{{dy}}{{dx}}\:+\mathrm{12}{y}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:{y}'''−\mathrm{3}{y}''+\mathrm{4}{y}'−\mathrm{2}{y}=\:{e}^{{x}} −\mathrm{cos}\:{x} \\ $$$$\left(\mathrm{3}\right){y}'''+\mathrm{3}{y}''+\mathrm{5}{y}'+\mathrm{3}{y}=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cot}\:\mathrm{4}{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$
Answered by bramlex last updated on 22/Jul/20
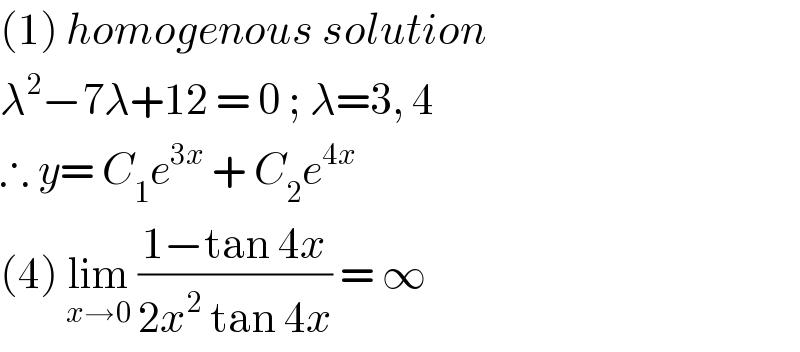
$$\left(\mathrm{1}\right)\:{homogenous}\:{solution} \\ $$$$\lambda^{\mathrm{2}} −\mathrm{7}\lambda+\mathrm{12}\:=\:\mathrm{0}\:;\:\lambda=\mathrm{3},\:\mathrm{4}\: \\ $$$$\therefore\:{y}=\:{C}_{\mathrm{1}} {e}^{\mathrm{3}{x}} \:+\:{C}_{\mathrm{2}} {e}^{\mathrm{4}{x}} \: \\ $$$$\left(\mathrm{4}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{tan}\:\mathrm{4}{x}}{\mathrm{2}{x}^{\mathrm{2}} \:\mathrm{tan}\:\mathrm{4}{x}}\:=\:\infty\: \\ $$
Answered by Dwaipayan Shikari last updated on 22/Jul/20
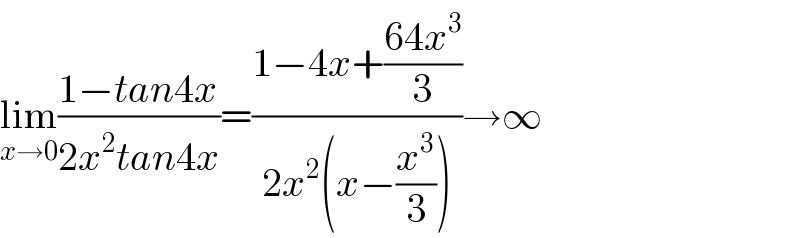
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{tan}\mathrm{4}{x}}{\mathrm{2}{x}^{\mathrm{2}} {tan}\mathrm{4}{x}}=\frac{\mathrm{1}−\mathrm{4}{x}+\frac{\mathrm{64}{x}^{\mathrm{3}} }{\mathrm{3}}}{\mathrm{2}{x}^{\mathrm{2}} \left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)}\rightarrow\infty \\ $$
