Menu Close

1-decompose-F-x-1-x-2-4-3-x-2-1-2-2-find-3-dx-x-2-4-3-x-2-1-2-

Tinku Tara 0 Comments
Pin




Question Number 130029 by mathmax by abdo last updated on 22/Jan/21
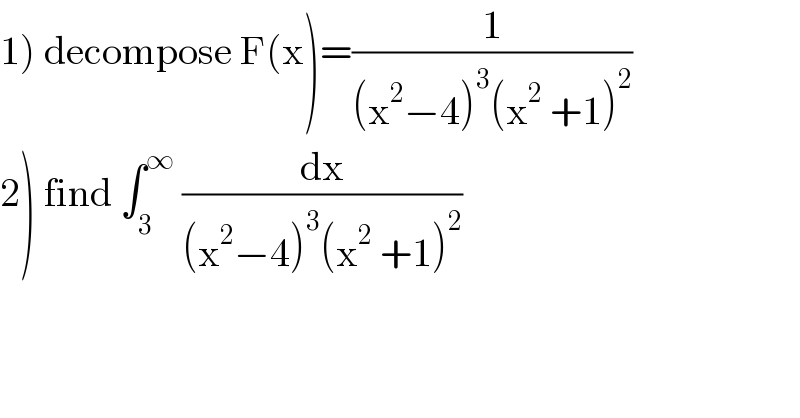
1) decompose F(x)=(1/((x^2 −4)^3 (x^2 +1)^2 )) 2) find ∫_3 ^∞ (dx/((x^2 −4)^3 (x^2 +1)^2 ))
$$\left.\mathrm{1}\right)\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\int_{\mathrm{3}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by MJS_new last updated on 22/Jan/21
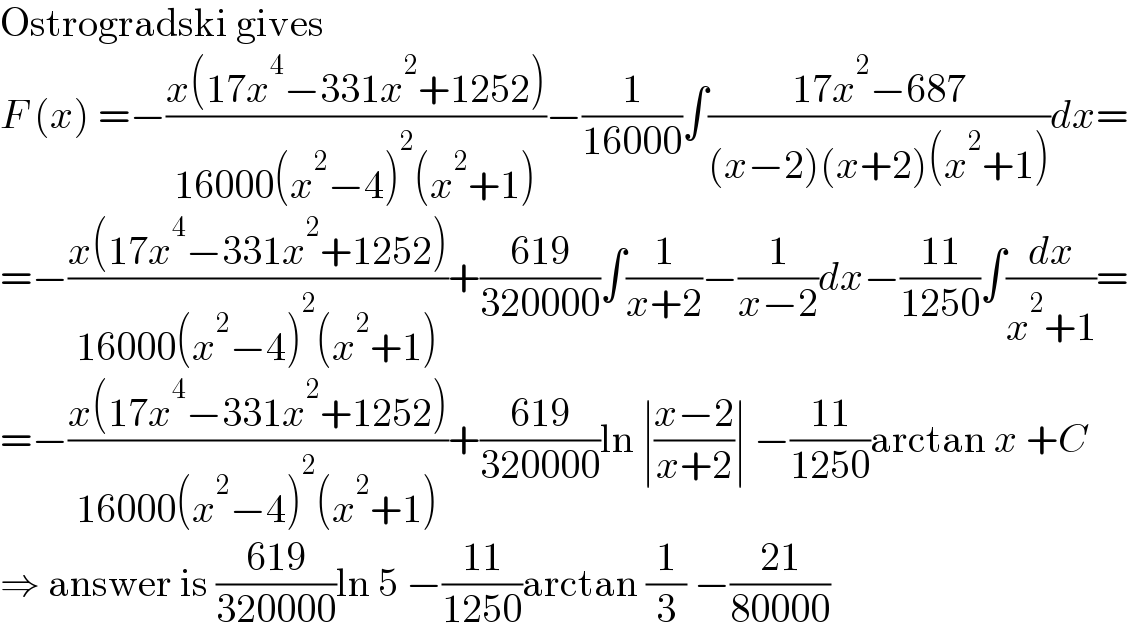
Ostrogradski gives F (x) =−((x(17x^4 −331x^2 +1252))/(16000(x^2 −4)^2 (x^2 +1)))−(1/(16000))∫((17x^2 −687)/((x−2)(x+2)(x^2 +1)))dx= =−((x(17x^4 −331x^2 +1252))/(16000(x^2 −4)^2 (x^2 +1)))+((619)/(320000))∫(1/(x+2))−(1/(x−2))dx−((11)/(1250))∫(dx/(x^2 +1))= =−((x(17x^4 −331x^2 +1252))/(16000(x^2 −4)^2 (x^2 +1)))+((619)/(320000))ln ∣((x−2)/(x+2))∣ −((11)/(1250))arctan x +C ⇒ answer is ((619)/(320000))ln 5 −((11)/(1250))arctan (1/3) −((21)/(80000))
$$\mathrm{Ostrogradski}\:\mathrm{gives} \\ $$$${F}\:\left({x}\right)\:=−\frac{{x}\left(\mathrm{17}{x}^{\mathrm{4}} −\mathrm{331}{x}^{\mathrm{2}} +\mathrm{1252}\right)}{\mathrm{16000}\left({x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{16000}}\int\frac{\mathrm{17}{x}^{\mathrm{2}} −\mathrm{687}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}= \\ $$$$=−\frac{{x}\left(\mathrm{17}{x}^{\mathrm{4}} −\mathrm{331}{x}^{\mathrm{2}} +\mathrm{1252}\right)}{\mathrm{16000}\left({x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{619}}{\mathrm{320000}}\int\frac{\mathrm{1}}{{x}+\mathrm{2}}−\frac{\mathrm{1}}{{x}−\mathrm{2}}{dx}−\frac{\mathrm{11}}{\mathrm{1250}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=−\frac{{x}\left(\mathrm{17}{x}^{\mathrm{4}} −\mathrm{331}{x}^{\mathrm{2}} +\mathrm{1252}\right)}{\mathrm{16000}\left({x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{619}}{\mathrm{320000}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\mid\:−\frac{\mathrm{11}}{\mathrm{1250}}\mathrm{arctan}\:{x}\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{619}}{\mathrm{320000}}\mathrm{ln}\:\mathrm{5}\:−\frac{\mathrm{11}}{\mathrm{1250}}\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:−\frac{\mathrm{21}}{\mathrm{80000}} \\ $$
Commented by liberty last updated on 22/Jan/21
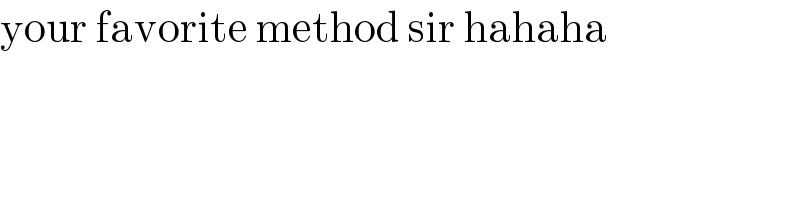
your favorite method sir hahaha
$$\mathrm{your}\:\mathrm{favorite}\:\mathrm{method}\:\mathrm{sir}\:\mathrm{hahaha} \\ $$
Answered by Ar Brandon last updated on 22/Jan/21
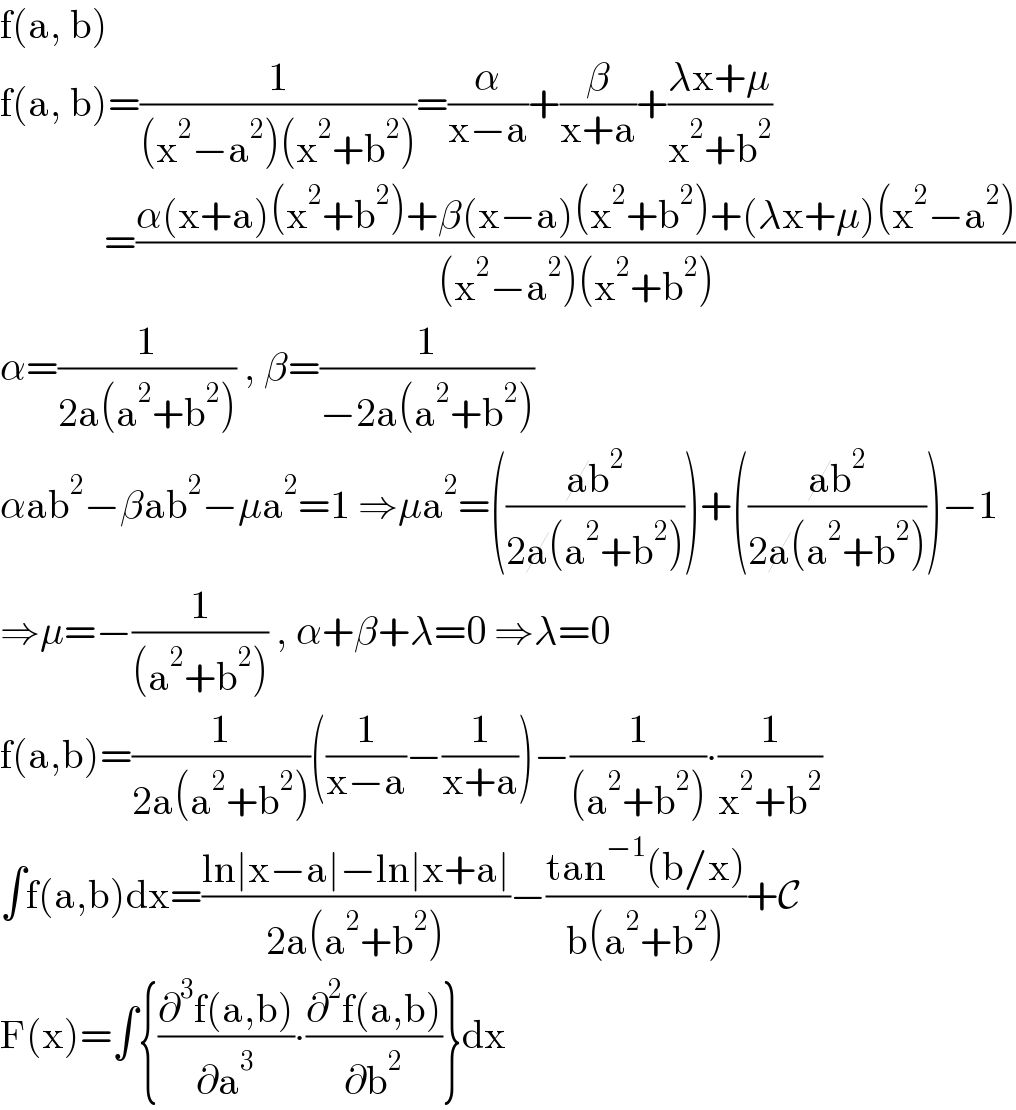
f(a, b) f(a, b)=(1/((x^2 −a^2 )(x^2 +b^2 )))=(α/(x−a))+(β/(x+a))+((λx+μ)/(x^2 +b^2 )) =((α(x+a)(x^2 +b^2 )+β(x−a)(x^2 +b^2 )+(λx+μ)(x^2 −a^2 ))/((x^2 −a^2 )(x^2 +b^2 ))) α=(1/(2a(a^2 +b^2 ))) , β=(1/(−2a(a^2 +b^2 ))) αab^2 −βab^2 −μa^2 =1 ⇒μa^2 =(((ab^2 )/(2a(a^2 +b^2 ))))+(((ab^2 )/(2a(a^2 +b^2 ))))−1 ⇒μ=−(1/((a^2 +b^2 ))) , α+β+λ=0 ⇒λ=0 f(a,b)=(1/(2a(a^2 +b^2 )))((1/(x−a))−(1/(x+a)))−(1/((a^2 +b^2 )))∙(1/(x^2 +b^2 )) ∫f(a,b)dx=((ln∣x−a∣−ln∣x+a∣)/(2a(a^2 +b^2 )))−((tan^(−1) (b/x))/(b(a^2 +b^2 )))+C F(x)=∫{((∂^3 f(a,b))/∂a^3 )∙((∂^2 f(a,b))/∂b^2 )}dx
$$\mathrm{f}\left(\mathrm{a},\:\mathrm{b}\right) \\ $$$$\mathrm{f}\left(\mathrm{a},\:\mathrm{b}\right)=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}=\frac{\alpha}{\mathrm{x}−\mathrm{a}}+\frac{\beta}{\mathrm{x}+\mathrm{a}}+\frac{\lambda\mathrm{x}+\mu}{\mathrm{x}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\alpha\left(\mathrm{x}+\mathrm{a}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)+\beta\left(\mathrm{x}−\mathrm{a}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)+\left(\lambda\mathrm{x}+\mu\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)} \\ $$$$\alpha=\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\:,\:\beta=\frac{\mathrm{1}}{−\mathrm{2a}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)} \\ $$$$\alpha\mathrm{ab}^{\mathrm{2}} −\beta\mathrm{ab}^{\mathrm{2}} −\mu\mathrm{a}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow\mu\mathrm{a}^{\mathrm{2}} =\left(\frac{\cancel{\mathrm{a}b}^{\mathrm{2}} }{\mathrm{2}\cancel{\mathrm{a}}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\right)+\left(\frac{\cancel{\mathrm{a}b}^{\mathrm{2}} }{\mathrm{2}\cancel{\mathrm{a}}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\right)−\mathrm{1} \\ $$$$\Rightarrow\mu=−\frac{\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\:,\:\alpha+\beta+\lambda=\mathrm{0}\:\Rightarrow\lambda=\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{a},\mathrm{b}\right)=\frac{\mathrm{1}}{\mathrm{2a}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{a}}\right)−\frac{\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\centerdot\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} } \\ $$$$\int\mathrm{f}\left(\mathrm{a},\mathrm{b}\right)\mathrm{dx}=\frac{\mathrm{ln}\mid\mathrm{x}−\mathrm{a}\mid−\mathrm{ln}\mid\mathrm{x}+\mathrm{a}\mid}{\mathrm{2a}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}−\frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{b}/\mathrm{x}\right)}{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}+\mathcal{C} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\int\left\{\frac{\partial^{\mathrm{3}} \mathrm{f}\left(\mathrm{a},\mathrm{b}\right)}{\partial\mathrm{a}^{\mathrm{3}} }\centerdot\frac{\partial^{\mathrm{2}} \mathrm{f}\left(\mathrm{a},\mathrm{b}\right)}{\partial\mathrm{b}^{\mathrm{2}} }\right\}\mathrm{dx} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *