Menu Close

1-decompose-F-x-1-x-4-x-3-5-2-calculate-5-dx-x-4-x-3-5-

Tinku Tara 0 Comments
Pin




Question Number 92971 by abdomathmax last updated on 10/May/20
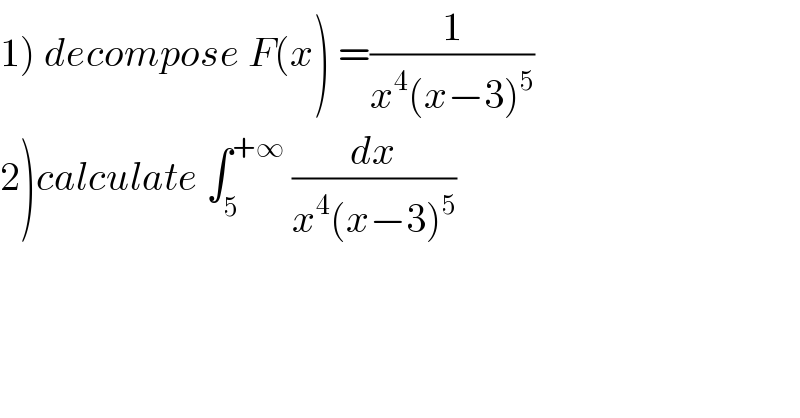
1) decompose F(x) =(1/(x^4 (x−3)^5 )) 2)calculate ∫_5 ^(+∞) (dx/(x^4 (x−3)^5 ))
$$\left.\mathrm{1}\right)\:{decompose}\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{{x}^{\mathrm{4}} \left({x}−\mathrm{3}\right)^{\mathrm{5}} } \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{5}} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \left({x}−\mathrm{3}\right)^{\mathrm{5}} } \\ $$
Commented by mathmax by abdo last updated on 11/May/20
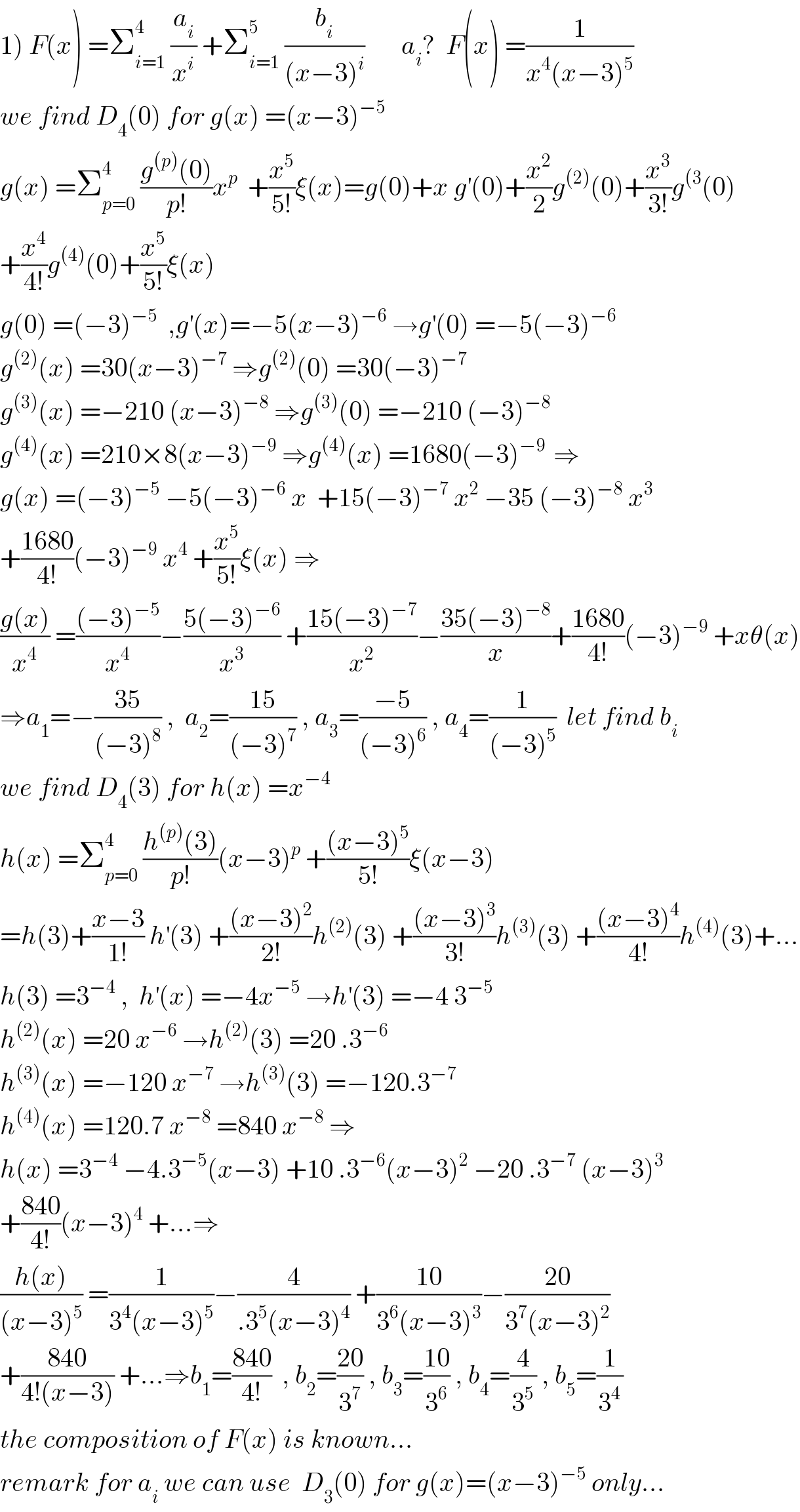
1) F(x) =Σ_(i=1) ^4 (a_i /x^i ) +Σ_(i=1) ^5 (b_i /((x−3)^i )) a_i ? F(x) =(1/(x^4 (x−3)^5 )) we find D_4 (0) for g(x) =(x−3)^(−5) g(x) =Σ_(p=0) ^4 ((g^((p)) (0))/(p!))x^p +(x^5 /(5!))ξ(x)=g(0)+x g^′ (0)+(x^2 /2)g^((2)) (0)+(x^3 /(3!))g^((3) (0) +(x^4 /(4!))g^((4)) (0)+(x^5 /(5!))ξ(x) g(0) =(−3)^(−5) ,g^′ (x)=−5(x−3)^(−6) →g^′ (0) =−5(−3)^(−6) g^((2)) (x) =30(x−3)^(−7) ⇒g^((2)) (0) =30(−3)^(−7) g^((3)) (x) =−210 (x−3)^(−8) ⇒g^((3)) (0) =−210 (−3)^(−8) g^((4)) (x) =210×8(x−3)^(−9) ⇒g^((4)) (x) =1680(−3)^(−9 ) ⇒ g(x) =(−3)^(−5) −5(−3)^(−6) x +15(−3)^(−7) x^2 −35 (−3)^(−8) x^3 +((1680)/(4!))(−3)^(−9) x^4 +(x^5 /(5!))ξ(x) ⇒ ((g(x))/x^4 ) =(((−3)^(−5) )/x^4 )−((5(−3)^(−6) )/x^3 ) +((15(−3)^(−7) )/x^2 )−((35(−3)^(−8) )/x)+((1680)/(4!))(−3)^(−9) +xθ(x) ⇒a_1 =−((35)/((−3)^8 )) , a_2 =((15)/((−3)^7 )) , a_3 =((−5)/((−3)^6 )) , a_4 =(1/((−3)^5 )) let find b_i we find D_4 (3) for h(x) =x^(−4) h(x) =Σ_(p=0) ^4 ((h^((p)) (3))/(p!))(x−3)^p +(((x−3)^5 )/(5!))ξ(x−3) =h(3)+((x−3)/(1!)) h^′ (3) +(((x−3)^2 )/(2!))h^((2)) (3) +(((x−3)^3 )/(3!))h^((3)) (3) +(((x−3)^4 )/(4!))h^((4)) (3)+... h(3) =3^(−4) , h^′ (x) =−4x^(−5) →h^′ (3) =−4 3^(−5) h^((2)) (x) =20 x^(−6) →h^((2)) (3) =20 .3^(−6) h^((3)) (x) =−120 x^(−7) →h^((3)) (3) =−120.3^(−7) h^((4)) (x) =120.7 x^(−8) =840 x^(−8) ⇒ h(x) =3^(−4) −4.3^(−5) (x−3) +10 .3^(−6) (x−3)^2 −20 .3^(−7) (x−3)^3 +((840)/(4!))(x−3)^4 +...⇒ ((h(x))/((x−3)^5 )) =(1/(3^4 (x−3)^5 ))−(4/(.3^5 (x−3)^4 )) +((10)/(3^6 (x−3)^3 ))−((20)/(3^7 (x−3)^2 )) +((840)/(4!(x−3))) +...⇒b_1 =((840)/(4!)) , b_2 =((20)/3^7 ) , b_3 =((10)/3^6 ) , b_4 =(4/3^5 ) , b_5 =(1/3^4 ) the composition of F(x) is known... remark for a_i we can use D_3 (0) for g(x)=(x−3)^(−5) only...
$$\left.\mathrm{1}\right)\:{F}\left({x}\right)\:=\sum_{{i}=\mathrm{1}} ^{\mathrm{4}} \:\frac{{a}_{{i}} }{{x}^{{i}} }\:+\sum_{{i}=\mathrm{1}} ^{\mathrm{5}} \:\frac{{b}_{{i}} }{\left({x}−\mathrm{3}\right)^{{i}} }\:\:\:\:\:\:\:{a}_{{i}} ?\:\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{{x}^{\mathrm{4}} \left({x}−\mathrm{3}\right)^{\mathrm{5}} } \\ $$$${we}\:{find}\:{D}_{\mathrm{4}} \left(\mathrm{0}\right)\:{for}\:{g}\left({x}\right)\:=\left({x}−\mathrm{3}\right)^{−\mathrm{5}} \\ $$$${g}\left({x}\right)\:=\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{{g}^{\left({p}\right)} \left(\mathrm{0}\right)}{{p}!}{x}^{{p}} \:\:+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\xi\left({x}\right)={g}\left(\mathrm{0}\right)+{x}\:{g}^{'} \left(\mathrm{0}\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{g}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}{g}^{\left(\mathrm{3}\right.} \left(\mathrm{0}\right) \\ $$$$+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}{g}^{\left(\mathrm{4}\right)} \left(\mathrm{0}\right)+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\xi\left({x}\right) \\ $$$${g}\left(\mathrm{0}\right)\:=\left(−\mathrm{3}\right)^{−\mathrm{5}} \:\:,{g}^{'} \left({x}\right)=−\mathrm{5}\left({x}−\mathrm{3}\right)^{−\mathrm{6}} \:\rightarrow{g}^{'} \left(\mathrm{0}\right)\:=−\mathrm{5}\left(−\mathrm{3}\right)^{−\mathrm{6}} \\ $$$${g}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\mathrm{30}\left({x}−\mathrm{3}\right)^{−\mathrm{7}} \:\Rightarrow{g}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{30}\left(−\mathrm{3}\right)^{−\mathrm{7}} \\ $$$${g}^{\left(\mathrm{3}\right)} \left({x}\right)\:=−\mathrm{210}\:\left({x}−\mathrm{3}\right)^{−\mathrm{8}} \:\Rightarrow{g}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)\:=−\mathrm{210}\:\left(−\mathrm{3}\right)^{−\mathrm{8}} \\ $$$${g}^{\left(\mathrm{4}\right)} \left({x}\right)\:=\mathrm{210}×\mathrm{8}\left({x}−\mathrm{3}\right)^{−\mathrm{9}} \:\Rightarrow{g}^{\left(\mathrm{4}\right)} \left({x}\right)\:=\mathrm{1680}\left(−\mathrm{3}\right)^{−\mathrm{9}\:} \:\Rightarrow \\ $$$${g}\left({x}\right)\:=\left(−\mathrm{3}\right)^{−\mathrm{5}} \:−\mathrm{5}\left(−\mathrm{3}\right)^{−\mathrm{6}} \:{x}\:\:+\mathrm{15}\left(−\mathrm{3}\right)^{−\mathrm{7}} \:{x}^{\mathrm{2}} \:−\mathrm{35}\:\left(−\mathrm{3}\right)^{−\mathrm{8}} \:{x}^{\mathrm{3}} \\ $$$$+\frac{\mathrm{1680}}{\mathrm{4}!}\left(−\mathrm{3}\right)^{−\mathrm{9}} \:{x}^{\mathrm{4}} \:+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\xi\left({x}\right)\:\Rightarrow \\ $$$$\frac{{g}\left({x}\right)}{{x}^{\mathrm{4}} }\:=\frac{\left(−\mathrm{3}\right)^{−\mathrm{5}} }{{x}^{\mathrm{4}} }−\frac{\mathrm{5}\left(−\mathrm{3}\right)^{−\mathrm{6}} }{{x}^{\mathrm{3}} }\:+\frac{\mathrm{15}\left(−\mathrm{3}\right)^{−\mathrm{7}} }{{x}^{\mathrm{2}} }−\frac{\mathrm{35}\left(−\mathrm{3}\right)^{−\mathrm{8}} }{{x}}+\frac{\mathrm{1680}}{\mathrm{4}!}\left(−\mathrm{3}\right)^{−\mathrm{9}} \:+{x}\theta\left({x}\right) \\ $$$$\Rightarrow{a}_{\mathrm{1}} =−\frac{\mathrm{35}}{\left(−\mathrm{3}\right)^{\mathrm{8}} }\:,\:\:{a}_{\mathrm{2}} =\frac{\mathrm{15}}{\left(−\mathrm{3}\right)^{\mathrm{7}} }\:,\:{a}_{\mathrm{3}} =\frac{−\mathrm{5}}{\left(−\mathrm{3}\right)^{\mathrm{6}} }\:,\:{a}_{\mathrm{4}} =\frac{\mathrm{1}}{\left(−\mathrm{3}\right)^{\mathrm{5}} }\:\:{let}\:{find}\:{b}_{{i}} \\ $$$${we}\:{find}\:{D}_{\mathrm{4}} \left(\mathrm{3}\right)\:{for}\:{h}\left({x}\right)\:={x}^{−\mathrm{4}} \: \\ $$$${h}\left({x}\right)\:=\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{{h}^{\left({p}\right)} \left(\mathrm{3}\right)}{{p}!}\left({x}−\mathrm{3}\right)^{{p}} \:+\frac{\left({x}−\mathrm{3}\right)^{\mathrm{5}} }{\mathrm{5}!}\xi\left({x}−\mathrm{3}\right) \\ $$$$={h}\left(\mathrm{3}\right)+\frac{{x}−\mathrm{3}}{\mathrm{1}!}\:{h}^{'} \left(\mathrm{3}\right)\:+\frac{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{2}!}{h}^{\left(\mathrm{2}\right)} \left(\mathrm{3}\right)\:+\frac{\left({x}−\mathrm{3}\right)^{\mathrm{3}} }{\mathrm{3}!}{h}^{\left(\mathrm{3}\right)} \left(\mathrm{3}\right)\:+\frac{\left({x}−\mathrm{3}\right)^{\mathrm{4}} }{\mathrm{4}!}{h}^{\left(\mathrm{4}\right)} \left(\mathrm{3}\right)+… \\ $$$${h}\left(\mathrm{3}\right)\:=\mathrm{3}^{−\mathrm{4}} \:,\:\:{h}^{'} \left({x}\right)\:=−\mathrm{4}{x}^{−\mathrm{5}} \:\rightarrow{h}^{'} \left(\mathrm{3}\right)\:=−\mathrm{4}\:\mathrm{3}^{−\mathrm{5}} \\ $$$${h}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\mathrm{20}\:{x}^{−\mathrm{6}} \:\rightarrow{h}^{\left(\mathrm{2}\right)} \left(\mathrm{3}\right)\:=\mathrm{20}\:.\mathrm{3}^{−\mathrm{6}} \\ $$$${h}^{\left(\mathrm{3}\right)} \left({x}\right)\:=−\mathrm{120}\:{x}^{−\mathrm{7}} \:\rightarrow{h}^{\left(\mathrm{3}\right)} \left(\mathrm{3}\right)\:=−\mathrm{120}.\mathrm{3}^{−\mathrm{7}} \\ $$$${h}^{\left(\mathrm{4}\right)} \left({x}\right)\:=\mathrm{120}.\mathrm{7}\:{x}^{−\mathrm{8}} \:=\mathrm{840}\:{x}^{−\mathrm{8}} \:\Rightarrow \\ $$$${h}\left({x}\right)\:=\mathrm{3}^{−\mathrm{4}} \:−\mathrm{4}.\mathrm{3}^{−\mathrm{5}} \left({x}−\mathrm{3}\right)\:+\mathrm{10}\:.\mathrm{3}^{−\mathrm{6}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} \:−\mathrm{20}\:.\mathrm{3}^{−\mathrm{7}} \:\left({x}−\mathrm{3}\right)^{\mathrm{3}} \\ $$$$+\frac{\mathrm{840}}{\mathrm{4}!}\left({x}−\mathrm{3}\right)^{\mathrm{4}} \:+…\Rightarrow \\ $$$$\frac{{h}\left({x}\right)}{\left({x}−\mathrm{3}\right)^{\mathrm{5}} }\:=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} \left({x}−\mathrm{3}\right)^{\mathrm{5}} }−\frac{\mathrm{4}}{.\mathrm{3}^{\mathrm{5}} \left({x}−\mathrm{3}\right)^{\mathrm{4}} }\:+\frac{\mathrm{10}}{\mathrm{3}^{\mathrm{6}} \left({x}−\mathrm{3}\right)^{\mathrm{3}} }−\frac{\mathrm{20}}{\mathrm{3}^{\mathrm{7}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$+\frac{\mathrm{840}}{\mathrm{4}!\left({x}−\mathrm{3}\right)}\:+…\Rightarrow{b}_{\mathrm{1}} =\frac{\mathrm{840}}{\mathrm{4}!}\:\:,\:{b}_{\mathrm{2}} =\frac{\mathrm{20}}{\mathrm{3}^{\mathrm{7}} }\:,\:{b}_{\mathrm{3}} =\frac{\mathrm{10}}{\mathrm{3}^{\mathrm{6}} }\:,\:{b}_{\mathrm{4}} =\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{5}} }\:,\:{b}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} } \\ $$$${the}\:{composition}\:{of}\:{F}\left({x}\right)\:{is}\:{known}… \\ $$$${remark}\:{for}\:{a}_{{i}} \:{we}\:{can}\:{use}\:\:{D}_{\mathrm{3}} \left(\mathrm{0}\right)\:{for}\:{g}\left({x}\right)=\left({x}−\mathrm{3}\right)^{−\mathrm{5}} \:{only}… \\ $$
Commented by abdomathmax last updated on 11/May/20
2) we can find this integral without using decomposition ! let I =∫_5 ^(+∞) (dx/(x^4 (x−3)^5 )) ⇒ I =∫_5 ^(+∞) (dx/(((x/(x−3)))^4 (x−3)^9 )) changement (x/(x−3)) =t give x =tx−3t ⇒(1−t)x =−3t ⇒x =((3t)/(t−1)) ⇒ (dx/dt) =((3(t−1)−3t)/((t−1)^2 )) =((−3)/((t−1)^2 )) and x−3 =((3t)/(t−1))−3 =((3t−3t+3)/(t−1)) =(3/((t−1))) ⇒ I =∫_(5/2) ^1 ((−3dt)/((t−1)^2 t^4 ((3/(t−1)))^9 )) =(1/3^8 )∫_1 ^(5/2) (((t−1)^9 )/((t−1)^(2 ) .t^4 ))dt =(1/3^8 ) ∫_1 ^(5/2) (((t−1)^7 )/t^4 )dt ⇒ 3^8 ×I =∫_1 ^(5/2) ((Σ_(k=0) ^7 C_7 ^k t^k (−1)^(7−k) )/t^4 )dt =−∫_1 ^(5/2) Σ_(k=0) ^7 (−1)^k C_7 ^k t^(k−4) dt =−Σ_(k=0 and k≠3) ^7 (−1)^k C_7 ^k [(1/(k−3))t^(k−3) ]_1 ^(5/2) + C_7 ^3 ∫_1 ^(5/2) (dt/t) =−Σ_(k=0 and k≠3) ^7 (((−1)^k )/(k−3)) C_7 ^k {((5/2))^(k−3) −1} +C_7 ^3 ln((5/2)) ⇒I = (1/3^8 ) Σ_(k=0) ^7 (((−1)^k C_7 ^k )/(k−3))(1−((5/2))^(k−3) ) +C_7 ^3 ln((5/2)) .
$$\left.\mathrm{2}\right)\:{we}\:{can}\:{find}\:{this}\:{integral}\:{without}\:{using} \\ $$$${decomposition}\:\:!\:\:{let}\:{I}\:=\int_{\mathrm{5}} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \left({x}−\mathrm{3}\right)^{\mathrm{5}} }\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{5}} ^{+\infty} \:\frac{{dx}}{\left(\frac{{x}}{{x}−\mathrm{3}}\right)^{\mathrm{4}} \left({x}−\mathrm{3}\right)^{\mathrm{9}} }\:\:{changement}\:\frac{{x}}{{x}−\mathrm{3}}\:={t}\:{give} \\ $$$${x}\:={tx}−\mathrm{3}{t}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}\:=−\mathrm{3}{t}\:\Rightarrow{x}\:=\frac{\mathrm{3}{t}}{{t}−\mathrm{1}}\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{\mathrm{3}\left({t}−\mathrm{1}\right)−\mathrm{3}{t}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{3}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:{and}\:{x}−\mathrm{3}\:=\frac{\mathrm{3}{t}}{{t}−\mathrm{1}}−\mathrm{3} \\ $$$$=\frac{\mathrm{3}{t}−\mathrm{3}{t}+\mathrm{3}}{{t}−\mathrm{1}}\:=\frac{\mathrm{3}}{\left({t}−\mathrm{1}\right)}\:\Rightarrow \\ $$$${I}\:\:=\int_{\frac{\mathrm{5}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\:\frac{−\mathrm{3}{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:{t}^{\mathrm{4}} \left(\frac{\mathrm{3}}{{t}−\mathrm{1}}\right)^{\mathrm{9}} }\:=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{8}} }\int_{\mathrm{1}} ^{\frac{\mathrm{5}}{\mathrm{2}}} \:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{9}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}\:} .{t}^{\mathrm{4}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{8}} }\:\int_{\mathrm{1}} ^{\frac{\mathrm{5}}{\mathrm{2}}} \:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{7}} }{{t}^{\mathrm{4}} }{dt}\:\Rightarrow \\ $$$$\mathrm{3}^{\mathrm{8}} \:×{I}\:=\int_{\mathrm{1}} ^{\frac{\mathrm{5}}{\mathrm{2}}} \:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:{C}_{\mathrm{7}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{7}−{k}} }{{t}^{\mathrm{4}} }{dt} \\ $$$$=−\int_{\mathrm{1}} ^{\frac{\mathrm{5}}{\mathrm{2}}} \:\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:\left(−\mathrm{1}\right)^{{k}} \:\:{C}_{\mathrm{7}} ^{{k}} \:{t}^{{k}−\mathrm{4}} \:{dt} \\ $$$$=−\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{3}} ^{\mathrm{7}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{7}} ^{{k}} \:\:\left[\frac{\mathrm{1}}{{k}−\mathrm{3}}{t}^{{k}−\mathrm{3}} \right]_{\mathrm{1}} ^{\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$$+\:{C}_{\mathrm{7}} ^{\mathrm{3}} \:\int_{\mathrm{1}} ^{\frac{\mathrm{5}}{\mathrm{2}}} \:\frac{{dt}}{{t}} \\ $$$$=−\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{3}} ^{\mathrm{7}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{3}}\:{C}_{\mathrm{7}} ^{{k}} \:\left\{\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{{k}−\mathrm{3}} −\mathrm{1}\right\} \\ $$$$+{C}_{\mathrm{7}} ^{\mathrm{3}} \:{ln}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\: \\ $$$$\Rightarrow{I}\:=\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{8}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:\frac{\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{7}} ^{{k}} }{{k}−\mathrm{3}}\left(\mathrm{1}−\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{{k}−\mathrm{3}} \right) \\ $$$$+{C}_{\mathrm{7}} ^{\mathrm{3}} \:{ln}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:. \\ $$
Commented by abdomathmax last updated on 11/May/20
k≠3
$${k}\neq\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *