Question Number 104895 by mathmax by abdo last updated on 24/Jul/20
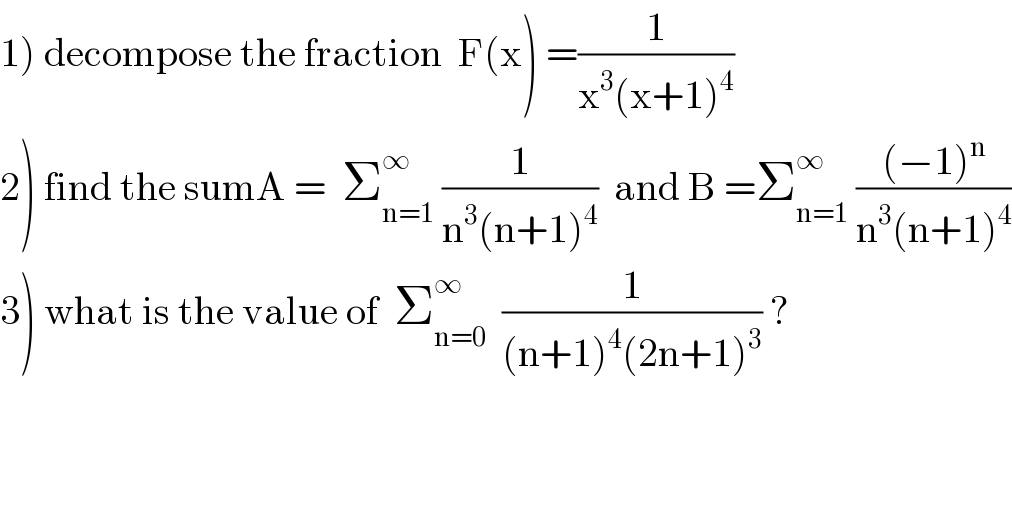
$$\left.\mathrm{1}\right)\:\mathrm{decompose}\:\mathrm{the}\:\mathrm{fraction}\:\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{sumA}\:=\:\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} }\:\:\mathrm{and}\:\mathrm{B}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{3}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\left.\mathrm{3}\right)\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:? \\ $$
Answered by Ar Brandon last updated on 25/Jul/20
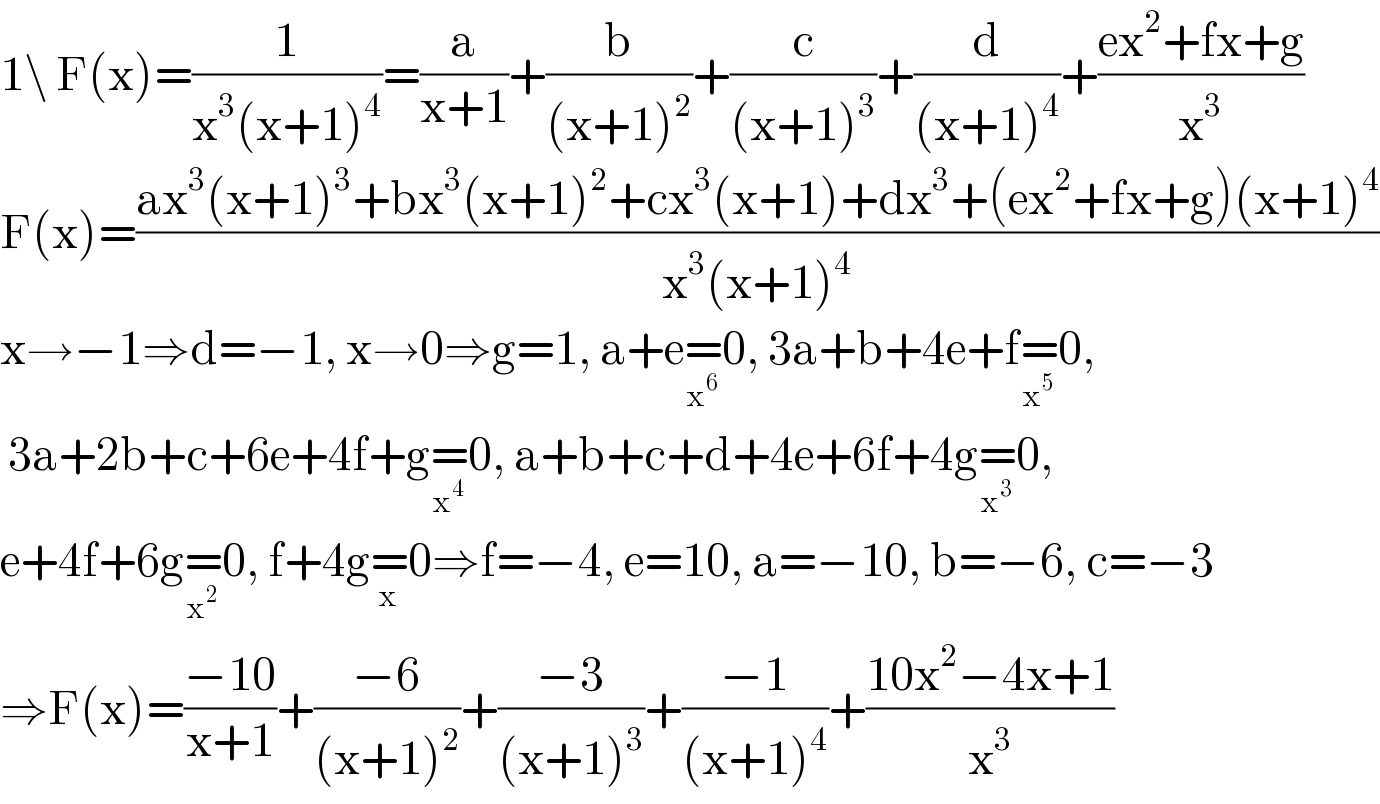
$$\mathrm{1}\backslash\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{b}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{c}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{d}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{ex}^{\mathrm{2}} +\mathrm{fx}+\mathrm{g}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{ax}^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} +\mathrm{bx}^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{cx}^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)+\mathrm{dx}^{\mathrm{3}} +\left(\mathrm{ex}^{\mathrm{2}} +\mathrm{fx}+\mathrm{g}\right)\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }{\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\mathrm{x}\rightarrow−\mathrm{1}\Rightarrow\mathrm{d}=−\mathrm{1},\:\mathrm{x}\rightarrow\mathrm{0}\Rightarrow\mathrm{g}=\mathrm{1},\:\mathrm{a}+\mathrm{e}\underset{\mathrm{x}^{\mathrm{6}} } {=}\mathrm{0},\:\mathrm{3a}+\mathrm{b}+\mathrm{4e}+\mathrm{f}\underset{\mathrm{x}^{\mathrm{5}} } {=}\mathrm{0}, \\ $$$$\:\mathrm{3a}+\mathrm{2b}+\mathrm{c}+\mathrm{6e}+\mathrm{4f}+\mathrm{g}\underset{\mathrm{x}^{\mathrm{4}} } {=}\mathrm{0},\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}+\mathrm{4e}+\mathrm{6f}+\mathrm{4g}\underset{\mathrm{x}^{\mathrm{3}} } {=}\mathrm{0}, \\ $$$$\mathrm{e}+\mathrm{4f}+\mathrm{6g}\underset{\mathrm{x}^{\mathrm{2}} } {=}\mathrm{0},\:\mathrm{f}+\mathrm{4g}\underset{\mathrm{x}} {=}\mathrm{0}\Rightarrow\mathrm{f}=−\mathrm{4},\:\mathrm{e}=\mathrm{10},\:\mathrm{a}=−\mathrm{10},\:\mathrm{b}=−\mathrm{6},\:\mathrm{c}=−\mathrm{3} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{−\mathrm{10}}{\mathrm{x}+\mathrm{1}}+\frac{−\mathrm{6}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{−\mathrm{3}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{−\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{10x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}}{\mathrm{x}^{\mathrm{3}} } \\ $$
Answered by mathmax by abdo last updated on 25/Jul/20
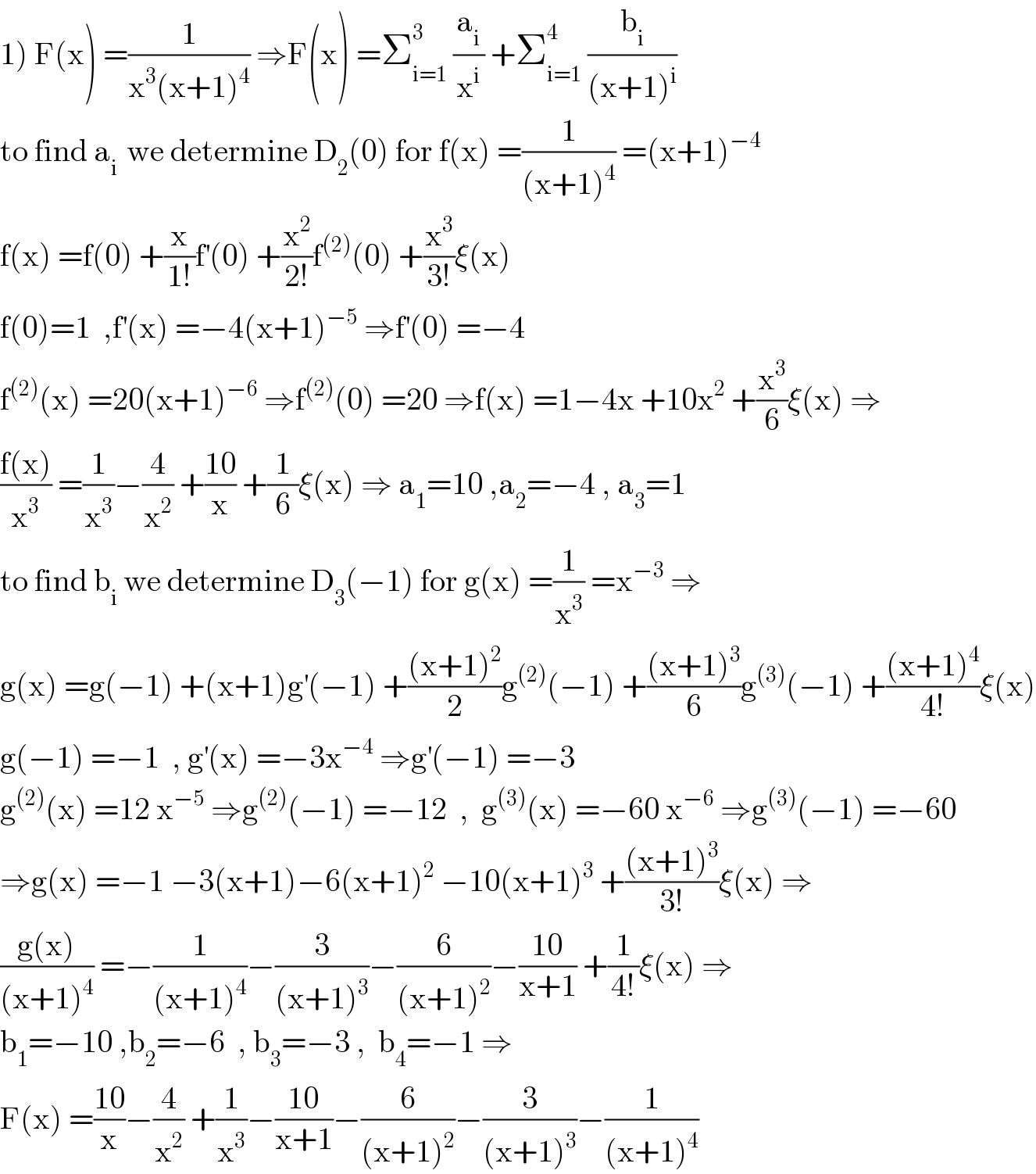
$$\left.\mathrm{1}\right)\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)\:=\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{3}} \:\frac{\mathrm{a}_{\mathrm{i}} }{\mathrm{x}^{\mathrm{i}} }\:+\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{4}} \:\frac{\mathrm{b}_{\mathrm{i}} }{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{i}} } \\ $$$$\mathrm{to}\:\mathrm{find}\:\mathrm{a}_{\mathrm{i}\:} \:\mathrm{we}\:\mathrm{determine}\:\mathrm{D}_{\mathrm{2}} \left(\mathrm{0}\right)\:\mathrm{for}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\:=\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{4}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{f}\left(\mathrm{0}\right)\:+\frac{\mathrm{x}}{\mathrm{1}!}\mathrm{f}^{'} \left(\mathrm{0}\right)\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\xi\left(\mathrm{x}\right) \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{1}\:\:,\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\mathrm{4}\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{5}} \:\Rightarrow\mathrm{f}^{'} \left(\mathrm{0}\right)\:=−\mathrm{4} \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\mathrm{20}\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{6}} \:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{20}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1}−\mathrm{4x}\:+\mathrm{10x}^{\mathrm{2}} \:+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\xi\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }−\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{10}}{\mathrm{x}}\:+\frac{\mathrm{1}}{\mathrm{6}}\xi\left(\mathrm{x}\right)\:\Rightarrow\:\mathrm{a}_{\mathrm{1}} =\mathrm{10}\:,\mathrm{a}_{\mathrm{2}} =−\mathrm{4}\:,\:\mathrm{a}_{\mathrm{3}} =\mathrm{1} \\ $$$$\mathrm{to}\:\mathrm{find}\:\mathrm{b}_{\mathrm{i}} \:\mathrm{we}\:\mathrm{determine}\:\mathrm{D}_{\mathrm{3}} \left(−\mathrm{1}\right)\:\mathrm{for}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:=\mathrm{x}^{−\mathrm{3}} \:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{g}\left(−\mathrm{1}\right)\:+\left(\mathrm{x}+\mathrm{1}\right)\mathrm{g}^{'} \left(−\mathrm{1}\right)\:+\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\mathrm{g}^{\left(\mathrm{2}\right)} \left(−\mathrm{1}\right)\:+\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{6}}\mathrm{g}^{\left(\mathrm{3}\right)} \left(−\mathrm{1}\right)\:+\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }{\mathrm{4}!}\xi\left(\mathrm{x}\right) \\ $$$$\mathrm{g}\left(−\mathrm{1}\right)\:=−\mathrm{1}\:\:,\:\mathrm{g}^{'} \left(\mathrm{x}\right)\:=−\mathrm{3x}^{−\mathrm{4}} \:\Rightarrow\mathrm{g}^{'} \left(−\mathrm{1}\right)\:=−\mathrm{3} \\ $$$$\mathrm{g}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\mathrm{12}\:\mathrm{x}^{−\mathrm{5}} \:\Rightarrow\mathrm{g}^{\left(\mathrm{2}\right)} \left(−\mathrm{1}\right)\:=−\mathrm{12}\:\:,\:\:\mathrm{g}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)\:=−\mathrm{60}\:\mathrm{x}^{−\mathrm{6}} \:\Rightarrow\mathrm{g}^{\left(\mathrm{3}\right)} \left(−\mathrm{1}\right)\:=−\mathrm{60} \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\:=−\mathrm{1}\:−\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{6}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{10}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \:+\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}!}\xi\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{g}\left(\mathrm{x}\right)}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\:=−\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{3}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{6}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{10}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}!}\xi\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{b}_{\mathrm{1}} =−\mathrm{10}\:,\mathrm{b}_{\mathrm{2}} =−\mathrm{6}\:\:,\:\mathrm{b}_{\mathrm{3}} =−\mathrm{3}\:,\:\:\mathrm{b}_{\mathrm{4}} =−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{10}}{\mathrm{x}}−\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }−\frac{\mathrm{10}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{6}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{3}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$
Commented by mathmax by abdo last updated on 25/Jul/20
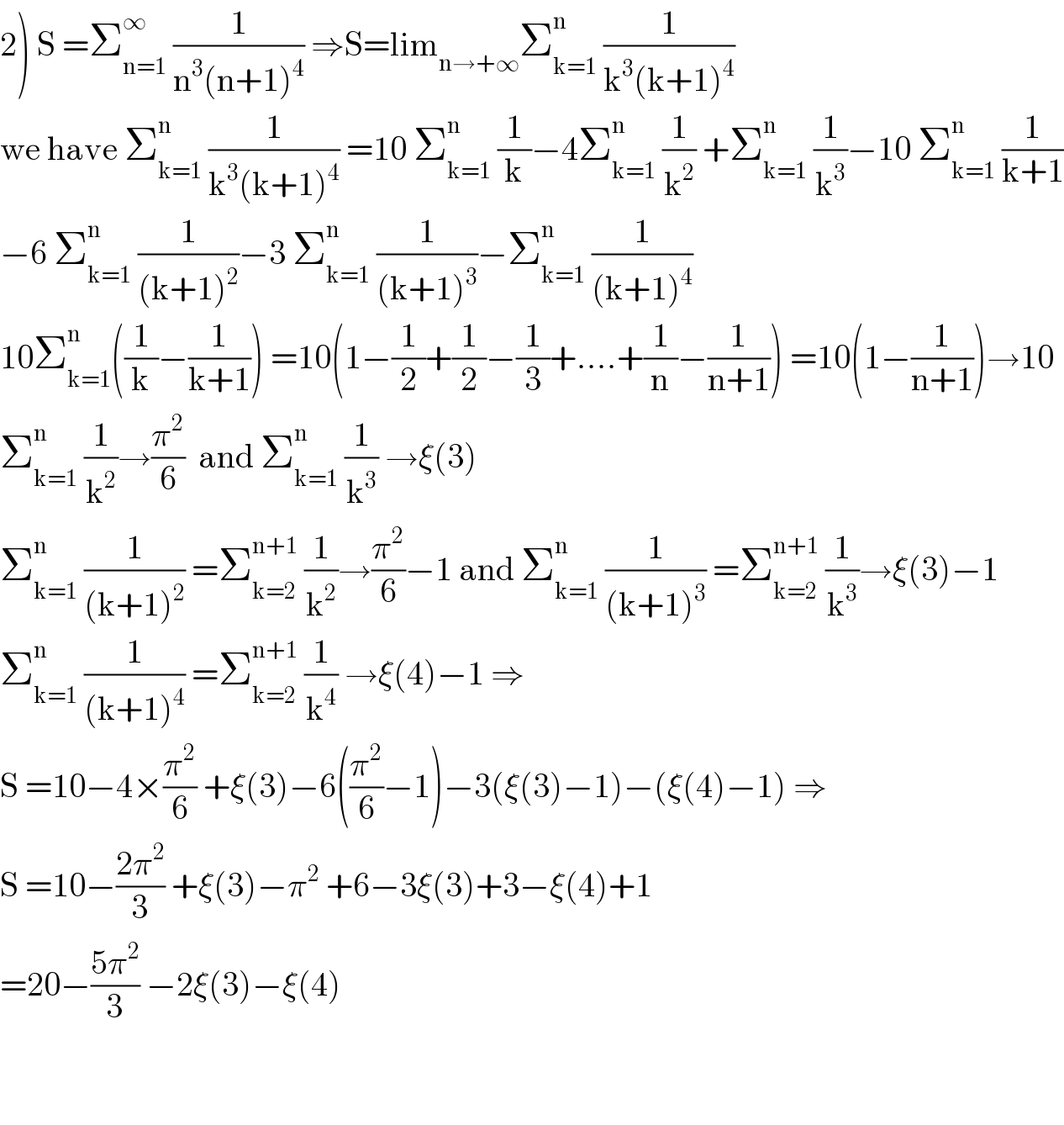
$$\left.\mathrm{2}\right)\:\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} }\:\Rightarrow\mathrm{S}=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} \left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} \left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{4}} }\:=\mathrm{10}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}−\mathrm{4}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\:+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} }−\mathrm{10}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}} \\ $$$$−\mathrm{6}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{3}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{3}} }−\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\mathrm{10}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right)\:=\mathrm{10}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+….+\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\:=\mathrm{10}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\rightarrow\mathrm{10} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\rightarrow\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:\mathrm{and}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} }\:\rightarrow\xi\left(\mathrm{3}\right) \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\rightarrow\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}\:\mathrm{and}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{3}} }\:=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} }\rightarrow\xi\left(\mathrm{3}\right)−\mathrm{1} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{4}} }\:=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{4}} }\:\rightarrow\xi\left(\mathrm{4}\right)−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{S}\:=\mathrm{10}−\mathrm{4}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:+\xi\left(\mathrm{3}\right)−\mathrm{6}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}\right)−\mathrm{3}\left(\xi\left(\mathrm{3}\right)−\mathrm{1}\right)−\left(\xi\left(\mathrm{4}\right)−\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{S}\:=\mathrm{10}−\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{3}}\:+\xi\left(\mathrm{3}\right)−\pi^{\mathrm{2}} \:+\mathrm{6}−\mathrm{3}\xi\left(\mathrm{3}\right)+\mathrm{3}−\xi\left(\mathrm{4}\right)+\mathrm{1} \\ $$$$=\mathrm{20}−\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{3}}\:−\mathrm{2}\xi\left(\mathrm{3}\right)−\xi\left(\mathrm{4}\right) \\ $$$$\: \\ $$$$ \\ $$
