Question Number 62754 by aliesam last updated on 24/Jun/19

$$\left.\mathrm{1}\right)\int\frac{{dx}}{\mathrm{1}−{sin}\left({x}\right)} \\ $$$$ \\ $$$${R}\:{solve}\:{in}\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{4}−{x}\right)^{\mathrm{4}} +{x}^{\mathrm{4}} =\mathrm{82} \\ $$
Commented by Tony Lin last updated on 25/Jun/19

$$\left(\mathrm{2}\right)\left(\mathrm{4}−{x}\right)^{\mathrm{4}} +{x}^{\mathrm{4}} =\mathrm{81}+\mathrm{1}=\mathrm{3}^{\mathrm{4}} +\mathrm{1}^{\mathrm{4}} \\ $$$${f}\left({x}\right)=\left(\mathrm{4}−{x}\right)^{\mathrm{4}} +{x}^{\mathrm{4}} −\mathrm{82} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0},\:{f}\left(\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}\left({x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{48}{x}^{\mathrm{2}} −\mathrm{128}{x}+\mathrm{87}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{29}\right) \\ $$$$\bigtriangleup=\left(−\mathrm{4}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{29}<\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{29}\:{has}\:{no}\:{roots}\:{in}\:{R} \\ $$$$\Rightarrow{x}=\mathrm{1}\:{or}\:{x}=\mathrm{3} \\ $$
Commented by mathmax by abdo last updated on 25/Jun/19
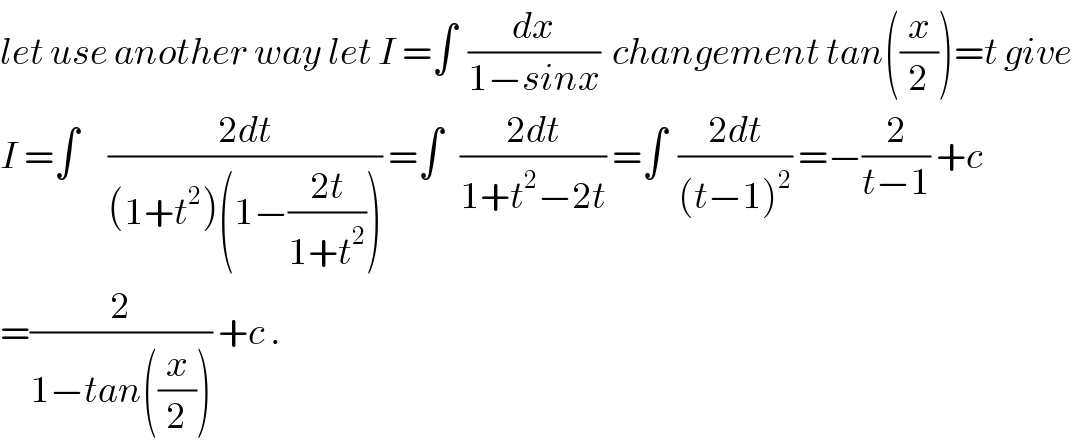
$${let}\:{use}\:{another}\:{way}\:{let}\:{I}\:=\int\:\:\frac{{dx}}{\mathrm{1}−{sinx}}\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int\:\:\:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\:=\int\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{t}}\:=\int\:\:\frac{\mathrm{2}{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{2}}{{t}−\mathrm{1}}\:+{c} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\:+{c}\:. \\ $$
Answered by Hope last updated on 25/Jun/19

$$\left.\mathrm{1}\right)\int\frac{\mathrm{1}+{sinx}}{{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int{sec}^{\mathrm{2}} {x}+{secxtanx}\:\:{dx} \\ $$$${tanx}+{secx}+{c} \\ $$
