Question Number 128279 by liberty last updated on 06/Jan/21
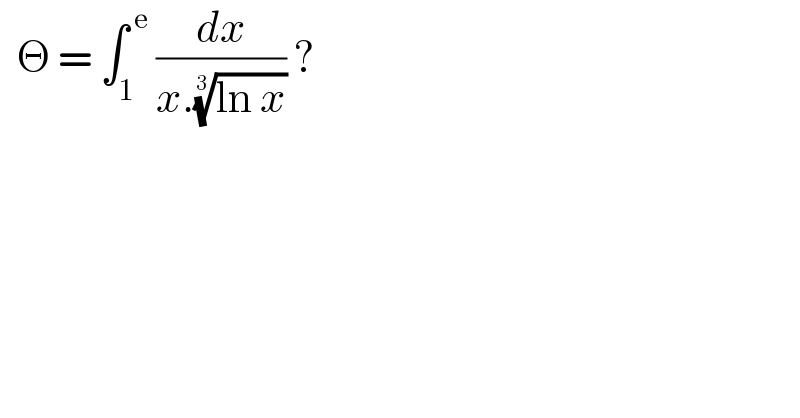
$$\:\:\Theta\:=\:\int_{\mathrm{1}} ^{\:\mathrm{e}} \:\frac{{dx}}{{x}.\sqrt[{\mathrm{3}}]{\mathrm{ln}\:{x}}}\:?\: \\ $$
Answered by john_santu last updated on 06/Jan/21
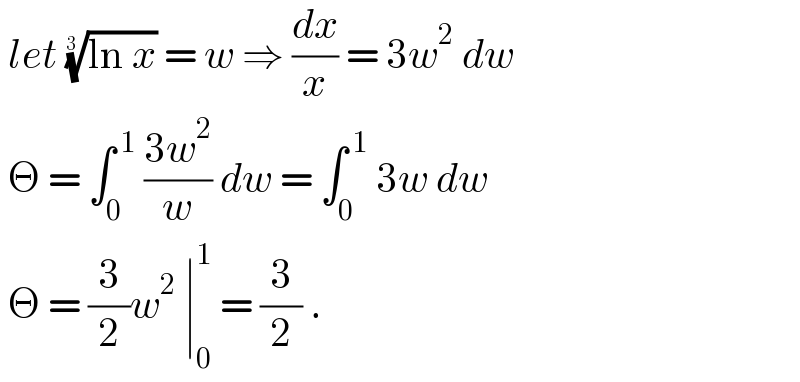
$$\:{let}\:\sqrt[{\mathrm{3}\:}]{\mathrm{ln}\:{x}}\:=\:{w}\:\Rightarrow\:\frac{{dx}}{{x}}\:=\:\mathrm{3}{w}^{\mathrm{2}} \:{dw} \\ $$$$\:\Theta\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{3}{w}^{\mathrm{2}} }{{w}}\:{dw}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\mathrm{3}{w}\:{dw}\:\: \\ $$$$\:\Theta\:=\:\frac{\mathrm{3}}{\mathrm{2}}{w}^{\mathrm{2}} \:\mid_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\mathrm{3}}{\mathrm{2}}\:. \\ $$
