Question Number 88902 by M±th+et£s last updated on 13/Apr/20

$$\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} {ln}\mid{x}\mid\:{dx} \\ $$
Commented by abdomathmax last updated on 13/Apr/20
![∫_(1/e) ^e ln∣x∣dx =[xlnx−x]_(1/e) ^e =(e−e)−(−(1/e)−(1/e)) =(2/e)](https://www.tinkutara.com/question/Q88911.png)
$$\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:{ln}\mid{x}\mid{dx}\:=\left[{xlnx}−{x}\right]_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:=\left({e}−{e}\right)−\left(−\frac{\mathrm{1}}{{e}}−\frac{\mathrm{1}}{{e}}\right) \\ $$$$=\frac{\mathrm{2}}{{e}} \\ $$
Commented by abdomathmax last updated on 13/Apr/20
![another way let λ>0 we have ∣x∣=x ⇒ ∫_(1/λ) ^λ ln(x)dx =[xlnx −x]_(1/λ) ^λ =λ lnλ−λ−((1/λ)ln((1/λ))−(1/λ)) =λln(λ)−λ+((ln(λ))/λ) +(1/λ) λ=e ⇒∫_(1/e) ^e ln(x)dx =e−e+(1/e)+(1/e) =(2/e)](https://www.tinkutara.com/question/Q88912.png)
$${another}\:{way}\:{let}\:\lambda>\mathrm{0}\:\:{we}\:{have}\:\:\mid{x}\mid={x}\:\Rightarrow \\ $$$$\int_{\frac{\mathrm{1}}{\lambda}} ^{\lambda} \:{ln}\left({x}\right){dx}\:=\left[{xlnx}\:−{x}\right]_{\frac{\mathrm{1}}{\lambda}} ^{\lambda} \:=\lambda\:{ln}\lambda−\lambda−\left(\frac{\mathrm{1}}{\lambda}{ln}\left(\frac{\mathrm{1}}{\lambda}\right)−\frac{\mathrm{1}}{\lambda}\right) \\ $$$$=\lambda{ln}\left(\lambda\right)−\lambda+\frac{{ln}\left(\lambda\right)}{\lambda}\:+\frac{\mathrm{1}}{\lambda} \\ $$$$\lambda={e}\:\Rightarrow\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} \:{ln}\left({x}\right){dx}\:={e}−{e}+\frac{\mathrm{1}}{{e}}+\frac{\mathrm{1}}{{e}}\:=\frac{\mathrm{2}}{{e}} \\ $$
Commented by M±th+et£s last updated on 13/Apr/20

$${thank}\:{you}\:{sir} \\ $$
Commented by turbo msup by abdo last updated on 13/Apr/20

$${you}\:{are}\:{welcome} \\ $$
Answered by TANMAY PANACEA. last updated on 13/Apr/20
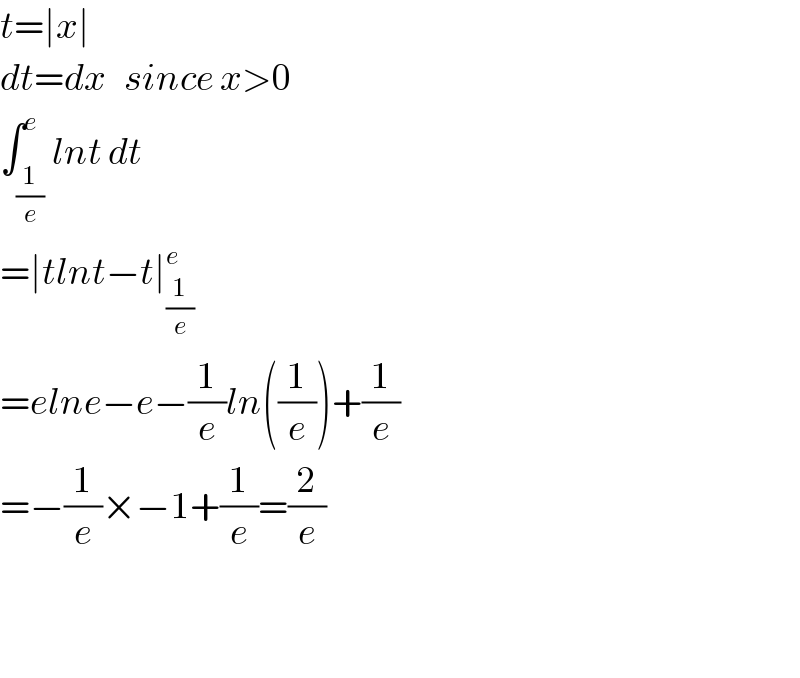
$${t}=\mid{x}\mid \\ $$$${dt}={dx}\:\:\:{since}\:{x}>\mathrm{0} \\ $$$$\int_{\frac{\mathrm{1}}{{e}}} ^{{e}} {lnt}\:{dt} \\ $$$$=\mid{tlnt}−{t}\mid_{\frac{\mathrm{1}}{{e}}} ^{{e}} \\ $$$$={elne}−{e}−\frac{\mathrm{1}}{{e}}{ln}\left(\frac{\mathrm{1}}{{e}}\right)+\frac{\mathrm{1}}{{e}} \\ $$$$=−\frac{\mathrm{1}}{{e}}×−\mathrm{1}+\frac{\mathrm{1}}{{e}}=\frac{\mathrm{2}}{{e}} \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 13/Apr/20

$${thank}\:{you}\:{sir} \\ $$
Commented by TANMAY PANACEA. last updated on 13/Apr/20

$${most}\:{welcome}\:{sir} \\ $$
