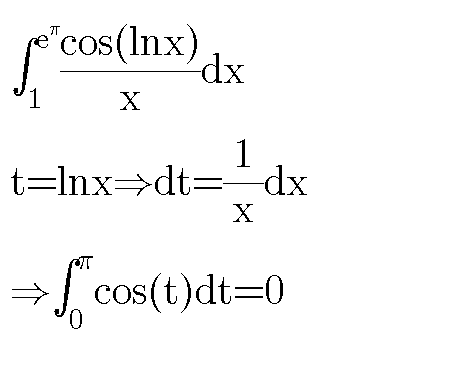Question Number 91904 by Ar Brandon last updated on 03/May/20
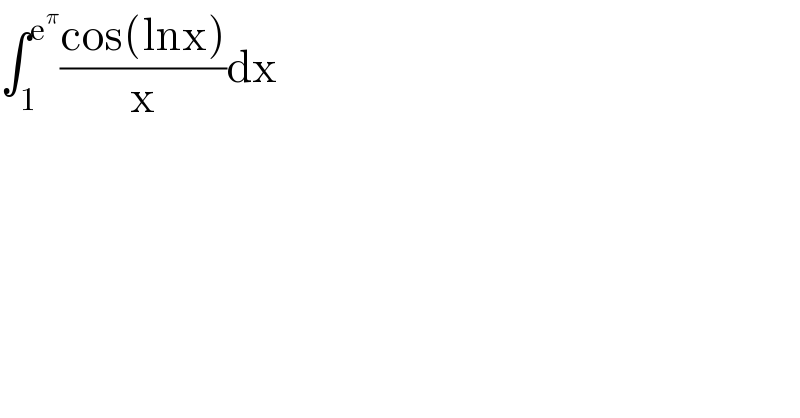
$$\int_{\mathrm{1}} ^{\mathrm{e}^{\pi} } \frac{\mathrm{cos}\left(\mathrm{lnx}\right)}{\mathrm{x}}\mathrm{dx} \\ $$
Commented by Prithwish Sen 1 last updated on 03/May/20

$$\mathrm{put}\:\mathrm{ln}\left(\mathrm{x}\right)=\mathrm{t} \\ $$
Commented by Ar Brandon last updated on 03/May/20
$$\mathrm{Okay},\:\mathrm{let}\:\mathrm{me}\:\mathrm{try}.\:\mathrm{Thanks} \\ $$
Commented by mathmax by abdo last updated on 03/May/20
![I =∫_1 ^e^π ((cos(lnx))/x)dx vhangement lnx =t give I =∫_0 ^π ((cos(t))/e^t ) e^t dt =∫_0 ^π cost dt =[sint]_0 ^π =0](https://www.tinkutara.com/question/Q91921.png)
$${I}\:=\int_{\mathrm{1}} ^{{e}^{\pi} } \:\frac{{cos}\left({lnx}\right)}{{x}}{dx}\:{vhangement}\:{lnx}\:={t}\:{give}\: \\ $$$${I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{cos}\left({t}\right)}{{e}^{{t}} }\:{e}^{{t}} \:{dt}\:=\int_{\mathrm{0}} ^{\pi} \:{cost}\:{dt}\:=\left[{sint}\right]_{\mathrm{0}} ^{\pi} \:=\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 03/May/20