Question Number 101816 by Dwaipayan Shikari last updated on 04/Jul/20
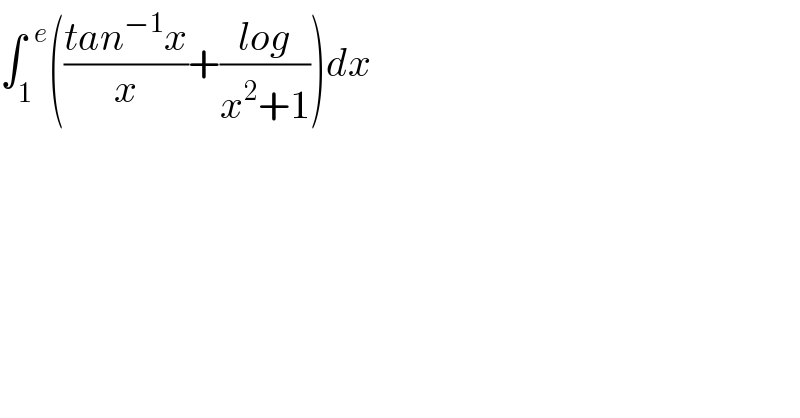
$$\int_{\mathrm{1}} ^{\:\:{e}} \left(\frac{{tan}^{−\mathrm{1}} {x}}{{x}}+\frac{{log}}{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx} \\ $$
Answered by Ar Brandon last updated on 05/Jul/20
![Let I=∫_1 ^e {((tan^(−1) x)/x)+((logx)/(x^2 +1))}dx (d/dx){tan^(−1) x∙logx}=((tan^(−1) x)/x)+((logx)/(1+x^2 )) ⇒I=∫_1 ^e d(tan^(−1) x∙logx)=[tan^(−1) x∙logx]_1 ^e =tan^(−1) (e)](https://www.tinkutara.com/question/Q101824.png)
$$\mathrm{Let}\:\mathcal{I}=\int_{\mathrm{1}} ^{\mathrm{e}} \left\{\frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{x}}{\mathrm{x}}+\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right\}\mathrm{dx} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left\{\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\centerdot\mathrm{logx}\right\}=\frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{x}}{\mathrm{x}}+\frac{\mathrm{logx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathcal{I}=\int_{\mathrm{1}} ^{\mathrm{e}} \mathrm{d}\left(\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\centerdot\mathrm{logx}\right)=\left[\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\centerdot\mathrm{logx}\right]_{\mathrm{1}} ^{\mathrm{e}} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}\right) \\ $$
