Menu Close

1-e-tanx-t-1-t-2-dt-1-e-cotx-1-t-1-t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 101378 by Rohit@Thakur last updated on 02/Jul/20
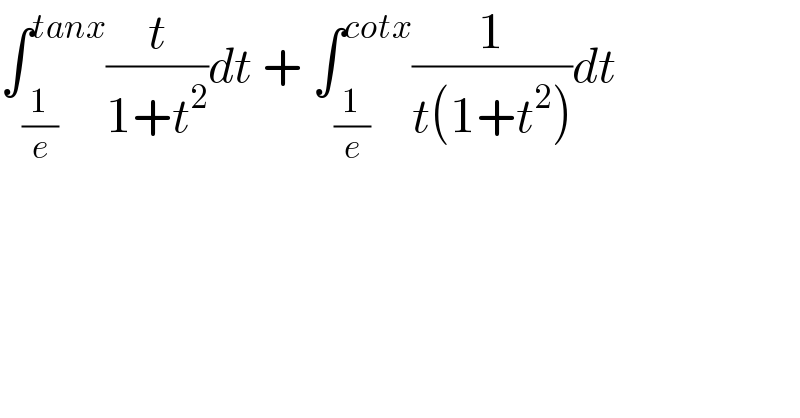
∫_(1/e) ^(tanx) (t/(1+t^2 ))dt + ∫_(1/e) ^(cotx) (1/(t(1+t^2 )))dt
$$\int_{\frac{\mathrm{1}}{{e}}} ^{{tanx}} \frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:+\:\int_{\frac{\mathrm{1}}{{e}}} ^{{cotx}} \frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$
Commented by Dwaipayan Shikari last updated on 02/Jul/20
(1/2)∫_(1/e) ^(tanx) ((2tdt)/(1+t^2 ))=[(1/2)log(1+t^2 )]_(1/e) ^(tanx) =(1/2)log(sec^2 x)−(1/2)log(((1+e^2 )/e^2 )) −(1/2)∫_(1/e) ^(cotx) (((−2dt)/t^3 )/(1+(1/t^2 )))=[−(1/2)log(1+(1/t^2 ))]_(1/e) ^(cotx) =−(1/2)log(((cosec^2 x)/(cot^2 x)))+(1/2)log(1+e^2 ) =−(1/2)log(sec^2 x)+(1/2)log(1+e^2 ) So ∫_(1/e) ^(tanx) (t/(1+t^2 ))+∫_(1/e) ^(cotx) (1/(t(1+t^2 )))=(1/2)log(1+e^2 )−(1/2)log(((1+e^2 )/e^2 )) =(1/2)loge^2 =1 ★■L
$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{1}}{{e}}} ^{{tanx}} \frac{\mathrm{2}{tdt}}{\mathrm{1}+{t}^{\mathrm{2}} }=\left[\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right]_{\frac{\mathrm{1}}{{e}}} ^{{tanx}} =\frac{\mathrm{1}}{\mathrm{2}}{log}\left({sec}^{\mathrm{2}} {x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}+{e}^{\mathrm{2}} }{{e}^{\mathrm{2}} }\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{1}}{{e}}} ^{{cotx}} \frac{\frac{−\mathrm{2}{dt}}{{t}^{\mathrm{3}} }}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}=\left[−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\right]_{\frac{\mathrm{1}}{{e}}} ^{{cotx}} =−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{{cosec}^{\mathrm{2}} {x}}{{cot}^{\mathrm{2}} {x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}+{e}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}{log}\left({sec}^{\mathrm{2}} {x}\right)+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}+{e}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$ \\ $$$${So}\:\:\int_{\frac{\mathrm{1}}{{e}}} ^{{tanx}} \frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\int_{\frac{\mathrm{1}}{{e}}} ^{{cotx}} \frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}+{e}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}+{e}^{\mathrm{2}} }{{e}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{loge}^{\mathrm{2}} =\mathrm{1}\:\:\:\:\:\:\:\bigstar\blacksquare\mathscr{L} \\ $$
Answered by 1549442205 last updated on 02/Jul/20
A=∫(t/(1+t^2 ))dt=(1/2)∫((d(1+t^2 ))/(1+t^2 ))=(1/2)ln(1+t^2 ) B=∫(dt/(t(1+t^2 ))).Putting t=tan u⇒dt ⇒ { ((dt=(1+t^2 )du)),((sin u=(√(1/(1+cot^2 u)))=(1/( (√(1+(1/t^2 )))))=(t/( (√(1+t^2 )))))) :} ⇒B=∫(du/(tan u))=∫((cos u)/(sin u))du=∫((dsin u)/(sin u)) =ln∣sin u∣=ln∣(t/( (√(1+t^2 ))))∣Hence, ∫_(1/e) ^(tanx) (t/(1+t^2 ))dt + ∫_(1/e) ^(cotx) (1/(t(1+t^2 )))dt= A(tan x)−A((1/e))+B(cotx)−B((1/e)) =(1/2)ln(1/(cos^2 x))−(1/2)ln(1+e^(−2) )+ln∣cos x∣ −ln(1/( (√(1+e^2 ))))=−(1/2)ln(1+e^(−2) )+ln(√(1+e^2 )) =ln((√(1+e^2 ))/( (√(1+e^(−2) ))))=lne=1
$$\mathrm{A}=\int\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right) \\ $$$$\mathrm{B}=\int\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}.\mathrm{Putting}\:\mathrm{t}=\mathrm{tan}\:\mathrm{u}\Rightarrow\mathrm{dt} \\ $$$$\:\Rightarrow\begin{cases}{\mathrm{dt}=\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{du}}\\{\mathrm{sin}\:\mathrm{u}=\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \mathrm{u}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}}=\frac{\mathrm{t}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}}\end{cases} \\ $$$$\Rightarrow\mathrm{B}=\int\frac{\mathrm{du}}{\mathrm{tan}\:\mathrm{u}}=\int\frac{\mathrm{cos}\:\mathrm{u}}{\mathrm{sin}\:\mathrm{u}}\mathrm{du}=\int\frac{\mathrm{dsin}\:\mathrm{u}}{\mathrm{sin}\:\mathrm{u}} \\ $$$$=\mathrm{ln}\mid\mathrm{sin}\:\mathrm{u}\mid=\mathrm{ln}\mid\frac{\mathrm{t}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\mid\mathrm{Hence}, \\ $$$$\int_{\frac{\mathrm{1}}{{e}}} ^{{tanx}} \frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:+\:\int_{\frac{\mathrm{1}}{{e}}} ^{{cotx}} \frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}= \\ $$$$\mathrm{A}\left(\mathrm{tan}\:\mathrm{x}\right)−\mathrm{A}\left(\frac{\mathrm{1}}{\mathrm{e}}\right)+\mathrm{B}\left(\mathrm{cotx}\right)−\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{e}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right)+\mathrm{ln}\mid\mathrm{cos}\:\mathrm{x}\mid \\ $$$$−\mathrm{ln}\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right)+\mathrm{ln}\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} } \\ $$$$=\boldsymbol{\mathrm{ln}}\frac{\sqrt{\mathrm{1}+\boldsymbol{\mathrm{e}}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+\boldsymbol{\mathrm{e}}^{−\mathrm{2}} }}=\boldsymbol{\mathrm{lne}}=\mathrm{1} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 02/Jul/20
we have ∫_(1/e) ^(tanx ) (t/(1+t^2 ))dt =[(1/2)ln(1+t^2 )]_(1/e) ^(tanx) =(1/2)ln(1+tan^2 x)−(1/2)ln(1+e^(−2) ) =(1/2)ln((1/(cos^2 x)))−(1/2)ln(1+e^(−2) ) =−ln∣cosx∣ −(1/2)ln(1+e^(−2) ) ∫_(1/e) ^(cotanx ) (dt/(t(1+t^2 ))) =∫_(1/e) ^(1/(tanx)) ((1/t)−(t/(1+t^2 )))dt =[ln∣t∣]_(1/e) ^(1/(tanx)) −[(1/2)ln(1+t^2 )]_(1/e) ^(1/(tanx)) =−ln∣tanx∣+1 −(1/2)ln(1+(1/(tan^2 x)))−(1/2)ln(1+e^(−2) ) =−ln∣tanx∣−(1/2)ln(1+tan^2 x)+ln∣tanx∣ −(1/2)ln(1+e^(−2) )+1 ⇒ ∫_(1/e) ^(tanx ) ((tdt)/(1+t^2 )) +∫_(1/e) ^(cotanx) (dt/(t(1+t^2 ))) = (1/2)ln(1+tan^2 x)−(1/2)ln(1+e^(−2) ) −(1/2)ln(1+tan^2 x)−(1/2)ln(1+e^(−2) ) +1 =1
$$\mathrm{we}\:\mathrm{have}\:\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{tanx}\:} \:\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right]_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{tanx}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right)\:=−\mathrm{ln}\mid\mathrm{cosx}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right) \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{cotanx}\:} \:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\frac{\mathrm{1}}{\mathrm{tanx}}} \:\left(\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt}\:=\left[\mathrm{ln}\mid\mathrm{t}\mid\right]_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\frac{\mathrm{1}}{\mathrm{tanx}}} \:−\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right]_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\frac{\mathrm{1}}{\mathrm{tanx}}} \\ $$$$=−\mathrm{ln}\mid\mathrm{tanx}\mid+\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right) \\ $$$$=−\mathrm{ln}\mid\mathrm{tanx}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{ln}\mid\mathrm{tanx}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right)+\mathrm{1}\:\Rightarrow \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{tanx}\:} \:\frac{\mathrm{tdt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{cotanx}} \:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2}} \right)\:+\mathrm{1}\:=\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *