Question Number 87325 by M±th+et£s last updated on 04/Apr/20
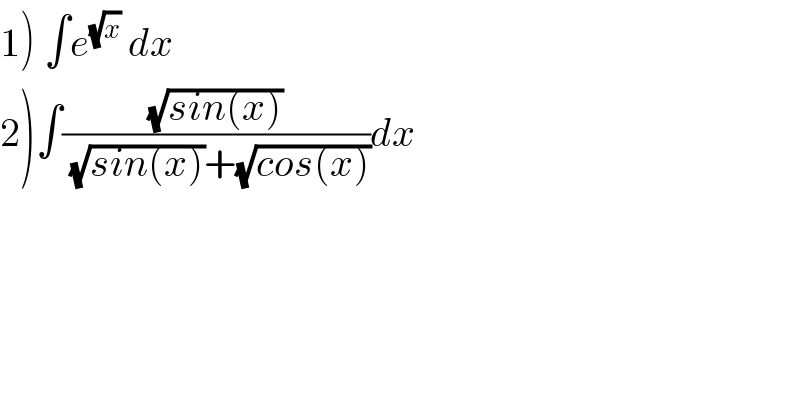
$$\left.\mathrm{1}\right)\:\int{e}^{\sqrt{{x}}} \:{dx} \\ $$$$\left.\mathrm{2}\right)\int\frac{\sqrt{{sin}\left({x}\right)}}{\:\sqrt{{sin}\left({x}\right)}+\sqrt{{cos}\left({x}\right)}}{dx} \\ $$
Commented by Serlea last updated on 04/Apr/20
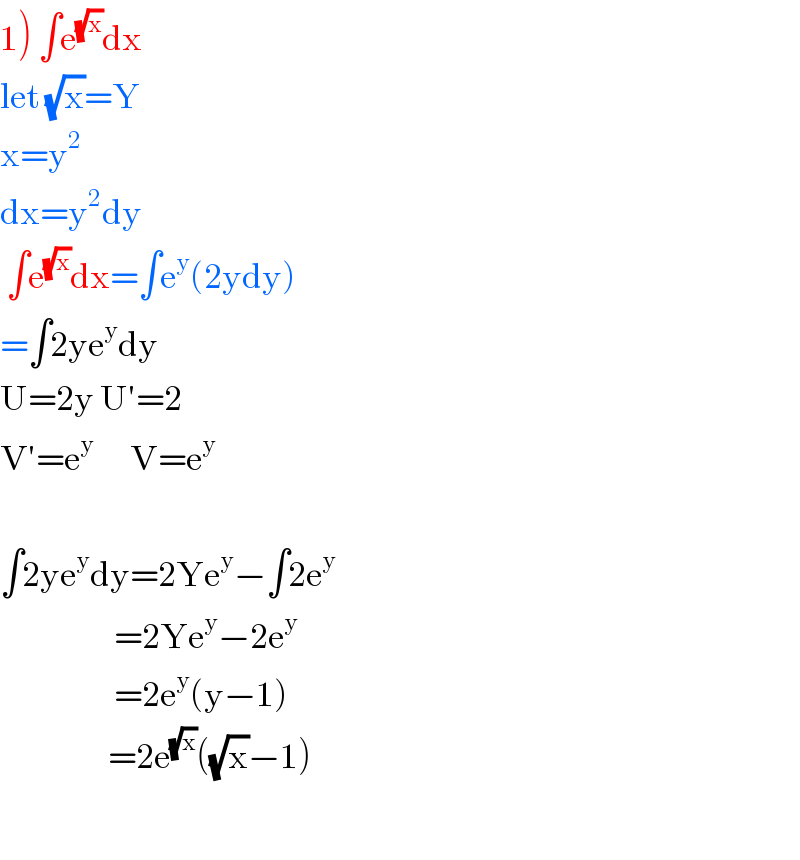
$$\left.\mathrm{1}\right)\:\int\mathrm{e}^{\sqrt{\mathrm{x}}} \mathrm{dx} \\ $$$$\mathrm{let}\:\sqrt{\mathrm{x}}=\mathrm{Y} \\ $$$$\mathrm{x}=\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{dx}=\mathrm{y}^{\mathrm{2}} \mathrm{dy} \\ $$$$\:\int\mathrm{e}^{\sqrt{\mathrm{x}}} \mathrm{dx}=\int\mathrm{e}^{\mathrm{y}} \left(\mathrm{2ydy}\right) \\ $$$$=\int\mathrm{2ye}^{\mathrm{y}} \mathrm{dy} \\ $$$$\mathrm{U}=\mathrm{2y}\:\mathrm{U}'=\mathrm{2} \\ $$$$\mathrm{V}'=\mathrm{e}^{\mathrm{y}} \:\:\:\:\:\:\mathrm{V}=\mathrm{e}^{\mathrm{y}} \\ $$$$ \\ $$$$\int\mathrm{2ye}^{\mathrm{y}} \mathrm{dy}=\mathrm{2Ye}^{\mathrm{y}} −\int\mathrm{2e}^{\mathrm{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2Ye}^{\mathrm{y}} −\mathrm{2e}^{\mathrm{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2e}^{\mathrm{y}} \left(\mathrm{y}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2e}^{\sqrt{\mathrm{x}}} \left(\sqrt{\mathrm{x}}−\mathrm{1}\right) \\ $$$$ \\ $$
Commented by peter frank last updated on 04/Apr/20

$${qn}\:\mathrm{2}\:{limit}\:? \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 04/Apr/20

$${no}\:{sir} \\ $$
Answered by MJS last updated on 04/Apr/20
![2) ∫((√(sin x))/( (√(sin x))+(√(cos x))))dx= [t=(√(tan x)) → dx=2cos^2 x (√(tan x))dt] =2∫(t^2 /((t^4 +1)(t+1)))dt= =−((1−(√2))/2)∫((t+1)/(t^2 −(√2)t+1))dt−((1+(√2))/2)∫((t+1)/(t^2 +(√2)t+1))dt+∫(dt/(t+1)) now it should be easy](https://www.tinkutara.com/question/Q87395.png)
$$\left.\mathrm{2}\right) \\ $$$$\int\frac{\sqrt{\mathrm{sin}\:{x}}}{\:\sqrt{\mathrm{sin}\:{x}}+\sqrt{\mathrm{cos}\:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\mathrm{2cos}^{\mathrm{2}} \:{x}\:\sqrt{\mathrm{tan}\:{x}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{4}} +\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{dt}= \\ $$$$=−\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}−\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}+\int\frac{{dt}}{{t}+\mathrm{1}} \\ $$$$\mathrm{now}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy} \\ $$
Commented by peter frank last updated on 04/Apr/20

$${thank}\:{you} \\ $$
Commented by M±th+et£s last updated on 04/Apr/20

$${thank}\:{you} \\ $$
