Menu Close

1-e-x-sinxdx-2-e-x-cosxdx-

Tinku Tara 0 Comments
Pin




Question Number 121046 by bounhome last updated on 05/Nov/20
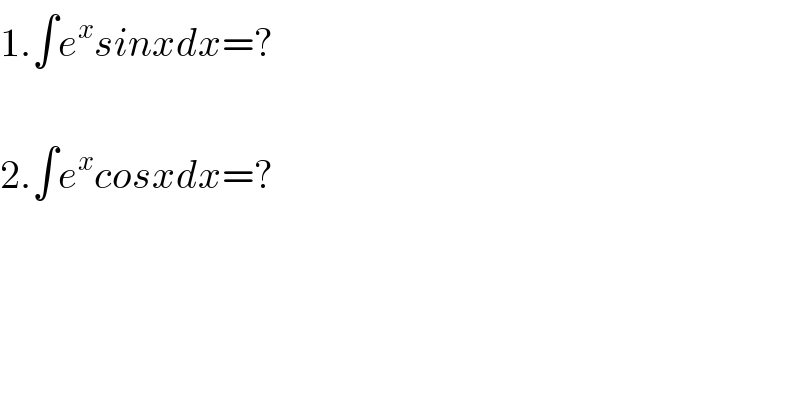
1.∫e^x sinxdx=? 2.∫e^x cosxdx=?
$$\mathrm{1}.\int{e}^{{x}} {sinxdx}=? \\ $$$$ \\ $$$$\mathrm{2}.\int{e}^{{x}} {cosxdx}=? \\ $$
Answered by Ar Brandon last updated on 05/Nov/20
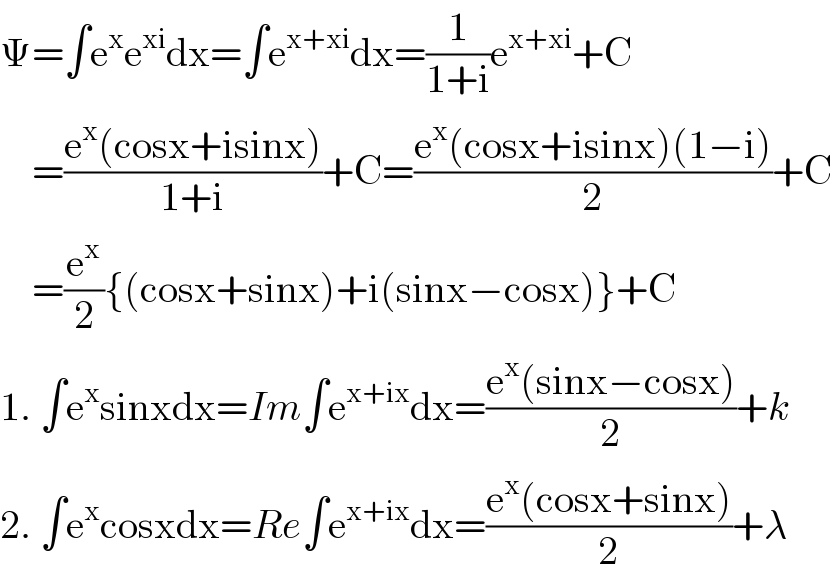
Ψ=∫e^x e^(xi) dx=∫e^(x+xi) dx=(1/(1+i))e^(x+xi) +C =((e^x (cosx+isinx))/(1+i))+C=((e^x (cosx+isinx)(1−i))/2)+C =(e^x /2){(cosx+sinx)+i(sinx−cosx)}+C 1. ∫e^x sinxdx=Im∫e^(x+ix) dx=((e^x (sinx−cosx))/2)+k 2. ∫e^x cosxdx=Re∫e^(x+ix) dx=((e^x (cosx+sinx))/2)+λ
$$\Psi=\int\mathrm{e}^{\mathrm{x}} \mathrm{e}^{\mathrm{xi}} \mathrm{dx}=\int\mathrm{e}^{\mathrm{x}+\mathrm{xi}} \mathrm{dx}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{i}}\mathrm{e}^{\mathrm{x}+\mathrm{xi}} +\mathrm{C} \\ $$$$\:\:\:\:=\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}+\mathrm{isinx}\right)}{\mathrm{1}+\mathrm{i}}+\mathrm{C}=\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}+\mathrm{isinx}\right)\left(\mathrm{1}−\mathrm{i}\right)}{\mathrm{2}}+\mathrm{C} \\ $$$$\:\:\:\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}\left\{\left(\mathrm{cosx}+\mathrm{sinx}\right)+\mathrm{i}\left(\mathrm{sinx}−\mathrm{cosx}\right)\right\}+\mathrm{C} \\ $$$$\mathrm{1}.\:\int\mathrm{e}^{\mathrm{x}} \mathrm{sinxdx}={Im}\int\mathrm{e}^{\mathrm{x}+\mathrm{ix}} \mathrm{dx}=\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{sinx}−\mathrm{cosx}\right)}{\mathrm{2}}+{k} \\ $$$$\mathrm{2}.\:\int\mathrm{e}^{\mathrm{x}} \mathrm{cosxdx}={Re}\int\mathrm{e}^{\mathrm{x}+\mathrm{ix}} \mathrm{dx}=\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}+\mathrm{sinx}\right)}{\mathrm{2}}+\lambda \\ $$
Answered by Ar Brandon last updated on 05/Nov/20
1. I=∫e^x sinxdx=sinx∫e^x dx−∫{((dsinx)/dx)∙∫e^x }dx =e^x sinx−∫e^x cosxdx=e^x sinx−[e^x cosx+∫e^x sinxdx] =((e^x (sinx−cosx))/2)+k
$$\mathrm{1}.\:\mathcal{I}=\int\mathrm{e}^{\mathrm{x}} \mathrm{sinxdx}=\mathrm{sinx}\int\mathrm{e}^{\mathrm{x}} \mathrm{dx}−\int\left\{\frac{\mathrm{dsinx}}{\mathrm{dx}}\centerdot\int\mathrm{e}^{\mathrm{x}} \right\}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{e}^{\mathrm{x}} \mathrm{sinx}−\int\mathrm{e}^{\mathrm{x}} \mathrm{cosxdx}=\mathrm{e}^{\mathrm{x}} \mathrm{sinx}−\left[\mathrm{e}^{\mathrm{x}} \mathrm{cosx}+\int\mathrm{e}^{\mathrm{x}} \mathrm{sinxdx}\right] \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{sinx}−\mathrm{cosx}\right)}{\mathrm{2}}+{k} \\ $$
Answered by ebi last updated on 05/Nov/20
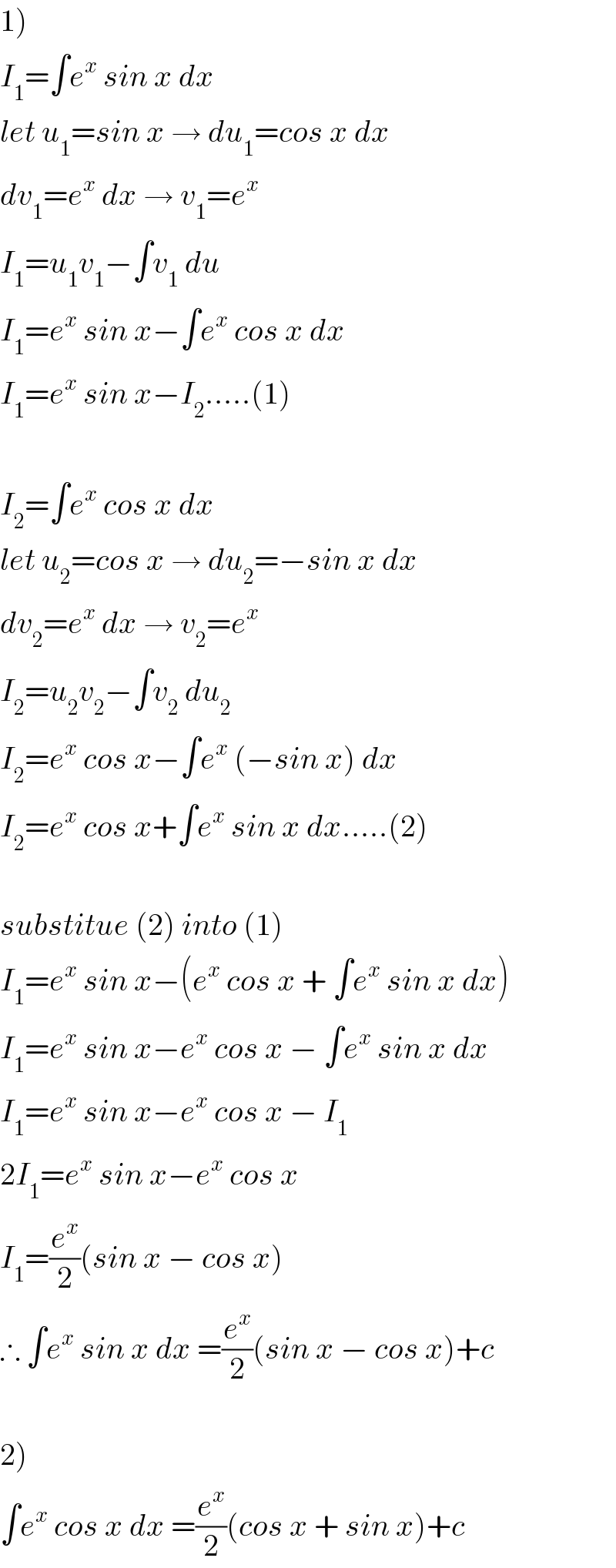
1) I_1 =∫e^x sin x dx let u_1 =sin x → du_1 =cos x dx dv_1 =e^x dx → v_1 =e^x I_1 =u_1 v_1 −∫v_1 du I_1 =e^x sin x−∫e^x cos x dx I_1 =e^x sin x−I_2 .....(1) I_2 =∫e^x cos x dx let u_2 =cos x → du_2 =−sin x dx dv_2 =e^x dx → v_2 =e^x I_2 =u_2 v_2 −∫v_2 du_2 I_2 =e^x cos x−∫e^x (−sin x) dx I_2 =e^x cos x+∫e^x sin x dx.....(2) substitue (2) into (1) I_1 =e^x sin x−(e^x cos x + ∫e^x sin x dx) I_1 =e^x sin x−e^x cos x − ∫e^x sin x dx I_1 =e^x sin x−e^x cos x − I_1 2I_1 =e^x sin x−e^x cos x I_1 =(e^x /2)(sin x − cos x) ∴ ∫e^x sin x dx =(e^x /2)(sin x − cos x)+c 2) ∫e^x cos x dx =(e^x /2)(cos x + sin x)+c
$$\left.\mathrm{1}\right) \\ $$$${I}_{\mathrm{1}} =\int{e}^{{x}} \:{sin}\:{x}\:{dx} \\ $$$${let}\:{u}_{\mathrm{1}} ={sin}\:{x}\:\rightarrow\:{du}_{\mathrm{1}} ={cos}\:{x}\:{dx} \\ $$$${dv}_{\mathrm{1}} ={e}^{{x}} \:{dx}\:\rightarrow\:{v}_{\mathrm{1}} ={e}^{{x}} \\ $$$${I}_{\mathrm{1}} ={u}_{\mathrm{1}} {v}_{\mathrm{1}} −\int{v}_{\mathrm{1}} \:{du} \\ $$$${I}_{\mathrm{1}} ={e}^{{x}} \:{sin}\:{x}−\int{e}^{{x}} \:{cos}\:{x}\:{dx} \\ $$$${I}_{\mathrm{1}} ={e}^{{x}} \:{sin}\:{x}−{I}_{\mathrm{2}} …..\left(\mathrm{1}\right) \\ $$$$ \\ $$$${I}_{\mathrm{2}} =\int{e}^{{x}} \:{cos}\:{x}\:{dx} \\ $$$${let}\:{u}_{\mathrm{2}} ={cos}\:{x}\:\rightarrow\:{du}_{\mathrm{2}} =−{sin}\:{x}\:{dx} \\ $$$${dv}_{\mathrm{2}} ={e}^{{x}} \:{dx}\:\rightarrow\:{v}_{\mathrm{2}} ={e}^{{x}} \\ $$$${I}_{\mathrm{2}} ={u}_{\mathrm{2}} {v}_{\mathrm{2}} −\int{v}_{\mathrm{2}} \:{du}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} ={e}^{{x}} \:{cos}\:{x}−\int{e}^{{x}} \:\left(−{sin}\:{x}\right)\:{dx} \\ $$$${I}_{\mathrm{2}} ={e}^{{x}} \:{cos}\:{x}+\int{e}^{{x}} \:{sin}\:{x}\:{dx}…..\left(\mathrm{2}\right) \\ $$$$ \\ $$$${substitue}\:\left(\mathrm{2}\right)\:{into}\:\left(\mathrm{1}\right) \\ $$$${I}_{\mathrm{1}} ={e}^{{x}} \:{sin}\:{x}−\left({e}^{{x}} \:{cos}\:{x}\:+\:\int{e}^{{x}} \:{sin}\:{x}\:{dx}\right) \\ $$$${I}_{\mathrm{1}} ={e}^{{x}} \:{sin}\:{x}−{e}^{{x}} \:{cos}\:{x}\:−\:\int{e}^{{x}} \:{sin}\:{x}\:{dx} \\ $$$${I}_{\mathrm{1}} ={e}^{{x}} \:{sin}\:{x}−{e}^{{x}} \:{cos}\:{x}\:−\:{I}_{\mathrm{1}} \\ $$$$\mathrm{2}{I}_{\mathrm{1}} ={e}^{{x}} \:{sin}\:{x}−{e}^{{x}} \:{cos}\:{x} \\ $$$${I}_{\mathrm{1}} =\frac{{e}^{{x}} }{\mathrm{2}}\left({sin}\:{x}\:−\:{cos}\:{x}\right) \\ $$$$\therefore\:\int{e}^{{x}} \:{sin}\:{x}\:{dx}\:=\frac{{e}^{{x}} }{\mathrm{2}}\left({sin}\:{x}\:−\:{cos}\:{x}\right)+{c} \\ $$$$ \\ $$$$\left.\mathrm{2}\right) \\ $$$$\int{e}^{{x}} \:{cos}\:{x}\:{dx}\:=\frac{{e}^{{x}} }{\mathrm{2}}\left({cos}\:{x}\:+\:{sin}\:{x}\right)+{c} \\ $$
Answered by n0y0n last updated on 05/Nov/20
USE DI Method
$$\mathrm{USE}\:\mathrm{DI}\:\mathrm{Method} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *