Menu Close

1-expicite-f-x-0-1-ln-1-xt-2-1-t-2-dt-with-x-0-2-calculate-0-1-ln-1-t-2-1-t-2-dt-and-0-1-ln-1-2t-2-1-t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 79627 by mathmax by abdo last updated on 26/Jan/20
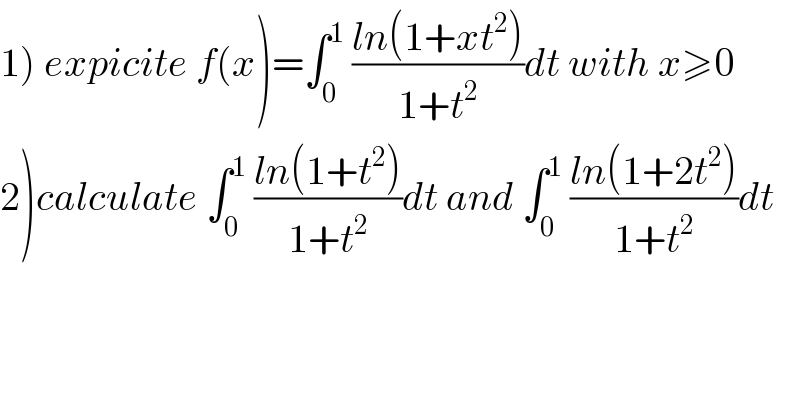
1) expicite f(x)=∫_0 ^1 ((ln(1+xt^2 ))/(1+t^2 ))dt with x≥0 2)calculate ∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt and ∫_0 ^1 ((ln(1+2t^2 ))/(1+t^2 ))dt
$$\left.\mathrm{1}\right)\:{expicite}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{xt}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{with}\:{x}\geqslant\mathrm{0} \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$
Commented by mathmax by abdo last updated on 30/Jan/20
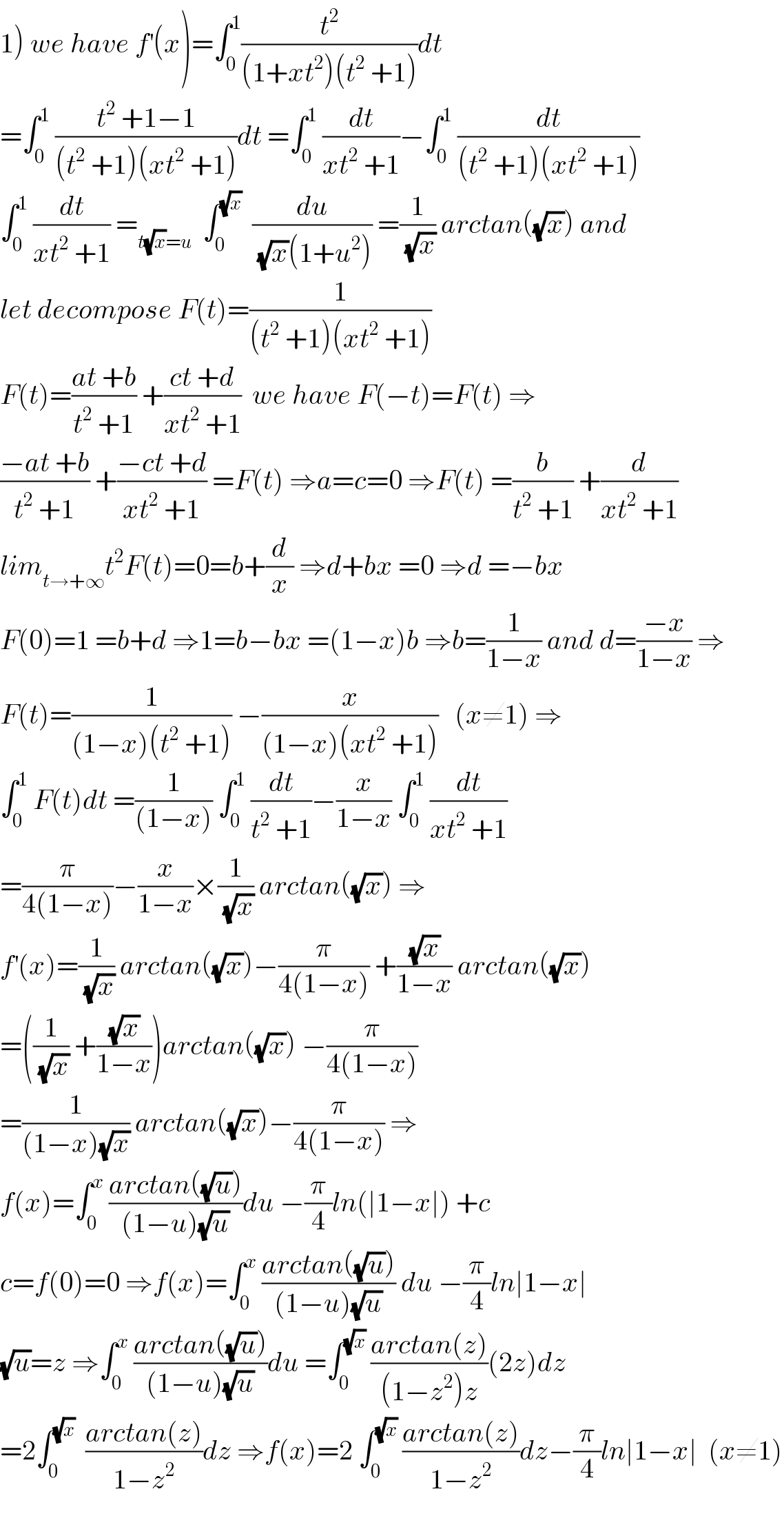
1) we have f^′ (x)=∫_0 ^1 (t^2 /((1+xt^2 )(t^2 +1)))dt =∫_0 ^1 ((t^2 +1−1)/((t^2 +1)(xt^2 +1)))dt =∫_0 ^1 (dt/(xt^2 +1))−∫_0 ^1 (dt/((t^2 +1)(xt^2 +1))) ∫_0 ^1 (dt/(xt^2 +1)) =_(t(√x)=u) ∫_0 ^(√x) (du/( (√x)(1+u^2 ))) =(1/( (√x))) arctan((√x)) and let decompose F(t)=(1/((t^2 +1)(xt^2 +1))) F(t)=((at +b)/(t^2 +1)) +((ct +d)/(xt^2 +1)) we have F(−t)=F(t) ⇒ ((−at +b)/(t^2 +1)) +((−ct +d)/(xt^2 +1)) =F(t) ⇒a=c=0 ⇒F(t) =(b/(t^2 +1)) +(d/(xt^2 +1)) lim_(t→+∞) t^2 F(t)=0=b+(d/x) ⇒d+bx =0 ⇒d =−bx F(0)=1 =b+d ⇒1=b−bx =(1−x)b ⇒b=(1/(1−x)) and d=((−x)/(1−x)) ⇒ F(t)=(1/((1−x)(t^2 +1))) −(x/((1−x)(xt^2 +1))) (x≠1) ⇒ ∫_0 ^1 F(t)dt =(1/((1−x))) ∫_0 ^1 (dt/(t^2 +1))−(x/(1−x)) ∫_0 ^1 (dt/(xt^2 +1)) =(π/(4(1−x)))−(x/(1−x))×(1/( (√x))) arctan((√x)) ⇒ f^′ (x)=(1/( (√x))) arctan((√x))−(π/(4(1−x))) +((√x)/(1−x)) arctan((√x)) =((1/( (√x))) +((√x)/(1−x)))arctan((√x)) −(π/(4(1−x))) =(1/((1−x)(√x))) arctan((√x))−(π/(4(1−x))) ⇒ f(x)=∫_0 ^x ((arctan((√u)))/((1−u)(√u)))du −(π/4)ln(∣1−x∣) +c c=f(0)=0 ⇒f(x)=∫_0 ^x ((arctan((√u)))/((1−u)(√u))) du −(π/4)ln∣1−x∣ (√u)=z ⇒∫_0 ^x ((arctan((√u)))/((1−u)(√u)))du =∫_0 ^(√x) ((arctan(z))/((1−z^2 )z))(2z)dz =2∫_0 ^(√x) ((arctan(z))/(1−z^2 ))dz ⇒f(x)=2 ∫_0 ^(√x) ((arctan(z))/(1−z^2 ))dz−(π/4)ln∣1−x∣ (x≠1)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{xt}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xt}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{xt}^{\mathrm{2}} \:+\mathrm{1}}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xt}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{xt}^{\mathrm{2}} \:+\mathrm{1}}\:=_{{t}\sqrt{{x}}={u}} \:\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\frac{{du}}{\:\sqrt{{x}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{arctan}\left(\sqrt{{x}}\right)\:{and} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)=\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xt}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${F}\left({t}\right)=\frac{{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ct}\:+{d}}{{xt}^{\mathrm{2}} \:+\mathrm{1}}\:\:{we}\:{have}\:{F}\left(−{t}\right)={F}\left({t}\right)\:\Rightarrow \\ $$$$\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{ct}\:+{d}}{{xt}^{\mathrm{2}} \:+\mathrm{1}}\:={F}\left({t}\right)\:\Rightarrow{a}={c}=\mathrm{0}\:\Rightarrow{F}\left({t}\right)\:=\frac{{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{d}}{{xt}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}^{\mathrm{2}} {F}\left({t}\right)=\mathrm{0}={b}+\frac{{d}}{{x}}\:\Rightarrow{d}+{bx}\:=\mathrm{0}\:\Rightarrow{d}\:=−{bx} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{1}\:={b}+{d}\:\Rightarrow\mathrm{1}={b}−{bx}\:=\left(\mathrm{1}−{x}\right){b}\:\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:{and}\:{d}=\frac{−{x}}{\mathrm{1}−{x}}\:\Rightarrow \\ $$$${F}\left({t}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:−\frac{{x}}{\left(\mathrm{1}−{x}\right)\left({xt}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:\:\left({x}\neq\mathrm{1}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}}−\frac{{x}}{\mathrm{1}−{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{xt}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{4}\left(\mathrm{1}−{x}\right)}−\frac{{x}}{\mathrm{1}−{x}}×\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{arctan}\left(\sqrt{{x}}\right)\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{arctan}\left(\sqrt{{x}}\right)−\frac{\pi}{\mathrm{4}\left(\mathrm{1}−{x}\right)}\:+\frac{\sqrt{{x}}}{\mathrm{1}−{x}}\:{arctan}\left(\sqrt{{x}}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\:\sqrt{{x}}}\:+\frac{\sqrt{{x}}}{\mathrm{1}−{x}}\right){arctan}\left(\sqrt{{x}}\right)\:−\frac{\pi}{\mathrm{4}\left(\mathrm{1}−{x}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\sqrt{{x}}}\:{arctan}\left(\sqrt{{x}}\right)−\frac{\pi}{\mathrm{4}\left(\mathrm{1}−{x}\right)}\:\Rightarrow \\ $$$${f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\frac{{arctan}\left(\sqrt{{u}}\right)}{\left(\mathrm{1}−{u}\right)\sqrt{{u}}}{du}\:−\frac{\pi}{\mathrm{4}}{ln}\left(\mid\mathrm{1}−{x}\mid\right)\:+{c} \\ $$$${c}={f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow{f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\frac{{arctan}\left(\sqrt{{u}}\right)}{\left(\mathrm{1}−{u}\right)\sqrt{{u}}}\:{du}\:−\frac{\pi}{\mathrm{4}}{ln}\mid\mathrm{1}−{x}\mid \\ $$$$\sqrt{{u}}={z}\:\Rightarrow\int_{\mathrm{0}} ^{{x}} \:\frac{{arctan}\left(\sqrt{{u}}\right)}{\left(\mathrm{1}−{u}\right)\sqrt{{u}}}{du}\:=\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\frac{{arctan}\left({z}\right)}{\left(\mathrm{1}−{z}^{\mathrm{2}} \right){z}}\left(\mathrm{2}{z}\right){dz} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\frac{{arctan}\left({z}\right)}{\mathrm{1}−{z}^{\mathrm{2}} }{dz}\:\Rightarrow{f}\left({x}\right)=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\frac{{arctan}\left({z}\right)}{\mathrm{1}−{z}^{\mathrm{2}} }{dz}−\frac{\pi}{\mathrm{4}}{ln}\mid\mathrm{1}−{x}\mid\:\:\left({x}\neq\mathrm{1}\right) \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 30/Jan/20
2)let A =∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt ⇒ A =∫_0 ^1 ((ln(1+it)+ln(1−it))/(1+t^2 ))dt =∫_0 ^1 ((ln(1+it))/(1+t^2 )) +conj(∫_0 ^1 ((ln(1+it))/(1+t^2 ))dt)=2Re (∫_0 ^1 ((ln(1+it))/(1+t^2 ))dt) let f(z)=∫_0 ^1 ((ln(1+zt))/(1+t^2 ))dt we have f^′ (z)=∫_0 ^1 (t/((1+zt)(t^2 +1)))dt decomposittion of F(t)=(t/((1+zt)(t^2 +1))) =(a/(zt +1)) +((bt +c)/(t^2 +1)) a =(zt+1)F(t)∣_(t=−(1/z)) =−(1/(z((1/z^2 )+1))) =−(1/(z(((1+z^2 )/z^2 )))) =−(z/(1+z^2 )) lim_(t→+∞) t F(t)=0 =(a/z) +b ⇒b=−(a/z) =(1/(1+z^2 )) F(0)=0 =a +c ⇒c=−a =(z/(1+z^2 )) ⇒ F(t)=−(z/((1+z^2 )(zt +1))) +(1/(1+z^2 ))×((t+z)/(t^2 +1)) ⇒ f^′ (z)=∫_0 ^1 F(t)dt =−(z/(1+z^2 )) ∫_0 ^1 (dt/(zt +1)) +(1/(2(1+z^2 )))∫_0 ^1 ((2t)/(t^2 +1))dt+(z/(1+z^2 ))∫_0 ^1 (dt/(1+t^2 )) =−(1/(1+z^2 ))ln(z+1)+(1/(2(1+z^2 )))ln(2)+(z/(1+z^2 ))×(π/4) ⇒ f(z) =−∫_0 ^z ((ln(1+u))/(u^2 +1)) du+((ln(2))/2)∫_0 ^z (du/(1+u^2 )) +(π/8) ∫_0 ^z ((2u)/(1+u^2 ))du +c =((ln(2))/2) arctan(z)+(π/8)ln(1+z^2 )−∫_0 ^z ((ln(1+u))/(u^2 +1))du (c=f(0)=0) f(1)=∫_0 ^1 ((ln(1+t))/(1+t^2 ))dt =((ln(2))/2)×(π/4) +(π/8)ln(2)−∫_0 ^1 ((ln(1+u))/(u^2 +1))du ⇒ 2 ∫_0 ^1 ((ln(1+u))/(1+u^2 ))du =(π/4)ln(2) ⇒∫_0 ^1 ((ln(1+u))/(1+u^2 ))du =(π/8)ln(2) the explicit form of f(x) dont give f(i)..so let try another way ....be continued...
$$\left.\mathrm{2}\right){let}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{it}\right)+{ln}\left(\mathrm{1}−{it}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{it}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:+{conj}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{it}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\right)=\mathrm{2}{Re}\:\left(\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{it}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\right) \\ $$$${let}\:{f}\left({z}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{zt}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:{we}\:{have}\:{f}^{'} \left({z}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}}{\left(\mathrm{1}+{zt}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt} \\ $$$${decomposittion}\:{of}\:{F}\left({t}\right)=\frac{{t}}{\left(\mathrm{1}+{zt}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{{a}}{{zt}\:+\mathrm{1}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:=\left({zt}+\mathrm{1}\right){F}\left({t}\right)\mid_{{t}=−\frac{\mathrm{1}}{{z}}} \:\:=−\frac{\mathrm{1}}{{z}\left(\frac{\mathrm{1}}{{z}^{\mathrm{2}} }+\mathrm{1}\right)}\:=−\frac{\mathrm{1}}{{z}\left(\frac{\mathrm{1}+{z}^{\mathrm{2}} }{{z}^{\mathrm{2}} }\right)}\:=−\frac{{z}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$${lim}_{{t}\rightarrow+\infty} \:{t}\:{F}\left({t}\right)=\mathrm{0}\:=\frac{{a}}{{z}}\:+{b}\:\Rightarrow{b}=−\frac{{a}}{{z}}\:=\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}\:={a}\:+{c}\:\Rightarrow{c}=−{a}\:=\frac{{z}}{\mathrm{1}+{z}^{\mathrm{2}} }\:\Rightarrow \\ $$$${F}\left({t}\right)=−\frac{{z}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left({zt}\:+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }×\frac{{t}+{z}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${f}^{'} \left({z}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({t}\right){dt}\:=−\frac{{z}}{\mathrm{1}+{z}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{zt}\:+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}+\frac{{z}}{\mathrm{1}+{z}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }{ln}\left({z}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}{ln}\left(\mathrm{2}\right)+\frac{{z}}{\mathrm{1}+{z}^{\mathrm{2}} }×\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$${f}\left({z}\right)\:=−\int_{\mathrm{0}} ^{{z}} \:\frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:{du}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\int_{\mathrm{0}} ^{{z}} \:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:+\frac{\pi}{\mathrm{8}}\:\int_{\mathrm{0}} ^{{z}} \:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:+{c} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:{arctan}\left({z}\right)+\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)−\int_{\mathrm{0}} ^{{z}} \:\frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}^{\mathrm{2}} \:+\mathrm{1}}{du}\:\left({c}={f}\left(\mathrm{0}\right)=\mathrm{0}\right) \\ $$$${f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}×\frac{\pi}{\mathrm{4}}\:+\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}^{\mathrm{2}} \:+\mathrm{1}}{du}\:\Rightarrow \\ $$$$\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$$${the}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right)\:{dont}\:{give}\:{f}\left({i}\right)..{so}\:{let}\:{try}\:{another}\:{way} \\ $$$$….{be}\:{continued}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *