Question Number 99146 by mathmax by abdo last updated on 18/Jun/20
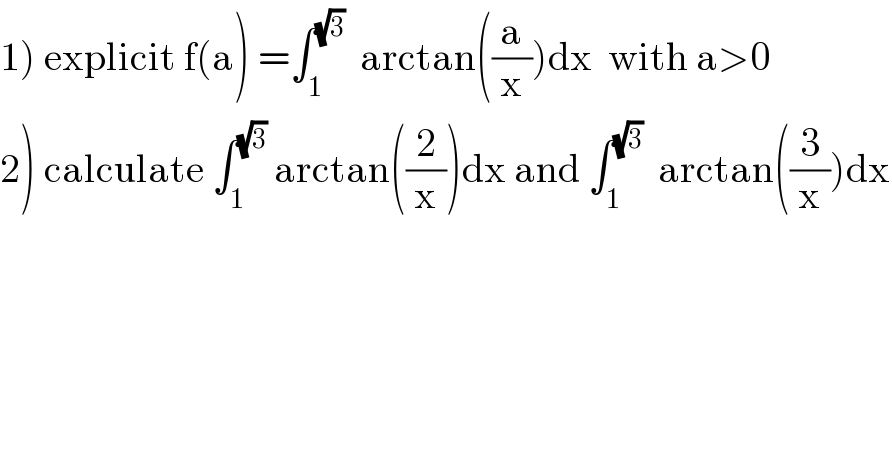
$$\left.\mathrm{1}\right)\:\mathrm{explicit}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{x}}\right)\mathrm{dx}\:\:\mathrm{with}\:\mathrm{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\mathrm{arctan}\left(\frac{\mathrm{2}}{\mathrm{x}}\right)\mathrm{dx}\:\mathrm{and}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 19/Jun/20
![1) f(a) =∫_1 ^(√3) arctan((a/x))dx by parts we get f(a) =[xarctan((a/x))]_1 ^(√3) −∫_1 ^(√3) x(−(a/x^2 ))×(1/(1+(a^2 /x^2 ))) dx =(√3)arctan((a/( (√3))))−arctan(a) +∫_1 ^(√3) ((ax)/(x^2 +a^2 )) dx but ∫_1 ^(√3) ((ax)/(x^2 +a^2 )) dx =_(x=au) ∫_(1/a) ^((√3)/a) ((a(au))/(a^2 (1+u^2 ))) adu =a ∫_(1/a) ^((√3)/a) ((udu)/(1+u^2 )) =(a/2)[ln(1+u^2 )]_(1/a) ^((√3)/a) =(a/2){ln(1+(3/a^2 ))−ln(1+(1/a^2 ))} =(a/2)ln(((a^2 +3)/(a^2 +1))) ⇒ f(a) =(√3)arctan((a/( (√3))))−arctan(a)+(a/2)ln(((3+a^2 )/(1+a^2 ))) 2)∫_1 ^(√3) artan((2/x))dx =f(2) =(√3) arctan((2/( (√3))))−arctan(2)+ln((7/5)) ∫_1 ^(√3) arctan((3/x))dx =f(3) =(√3) arctan((√3))−arctan(3)+(3/2)ln((6/5))](https://www.tinkutara.com/question/Q99216.png)
$$\left.\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\mathrm{arctan}\left(\frac{\mathrm{a}}{\mathrm{x}}\right)\mathrm{dx}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\left[\mathrm{xarctan}\left(\frac{\mathrm{a}}{\mathrm{x}}\right)\right]_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:−\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\mathrm{x}\left(−\frac{\mathrm{a}}{\mathrm{x}^{\mathrm{2}} }\right)×\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx} \\ $$$$=\sqrt{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{arctan}\left(\mathrm{a}\right)\:+\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\frac{\mathrm{ax}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\:\mathrm{dx}\:\:\mathrm{but} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{ax}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\:\mathrm{dx}\:=_{\mathrm{x}=\mathrm{au}} \:\:\:\int_{\frac{\mathrm{1}}{\mathrm{a}}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{a}}} \:\frac{\mathrm{a}\left(\mathrm{au}\right)}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\:\mathrm{adu}\:=\mathrm{a}\:\int_{\frac{\mathrm{1}}{\mathrm{a}}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{a}}} \:\frac{\mathrm{udu}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{a}}{\mathrm{2}}\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\right]_{\frac{\mathrm{1}}{\mathrm{a}}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{a}}} \:=\frac{\mathrm{a}}{\mathrm{2}}\left\{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{a}^{\mathrm{2}} }\right)−\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\right)\right\}\:=\frac{\mathrm{a}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{a}^{\mathrm{2}} \:+\mathrm{3}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\sqrt{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{arctan}\left(\mathrm{a}\right)+\frac{\mathrm{a}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{3}+\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\right) \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\mathrm{artan}\left(\frac{\mathrm{2}}{\mathrm{x}}\right)\mathrm{dx}\:=\mathrm{f}\left(\mathrm{2}\right)\:=\sqrt{\mathrm{3}}\:\mathrm{arctan}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{arctan}\left(\mathrm{2}\right)+\mathrm{ln}\left(\frac{\mathrm{7}}{\mathrm{5}}\right) \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\mathrm{dx}\:=\mathrm{f}\left(\mathrm{3}\right)\:=\sqrt{\mathrm{3}}\:\mathrm{arctan}\left(\sqrt{\mathrm{3}}\right)−\mathrm{arctan}\left(\mathrm{3}\right)+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{6}}{\mathrm{5}}\right) \\ $$
