Question Number 96373 by mathmax by abdo last updated on 01/Jun/20
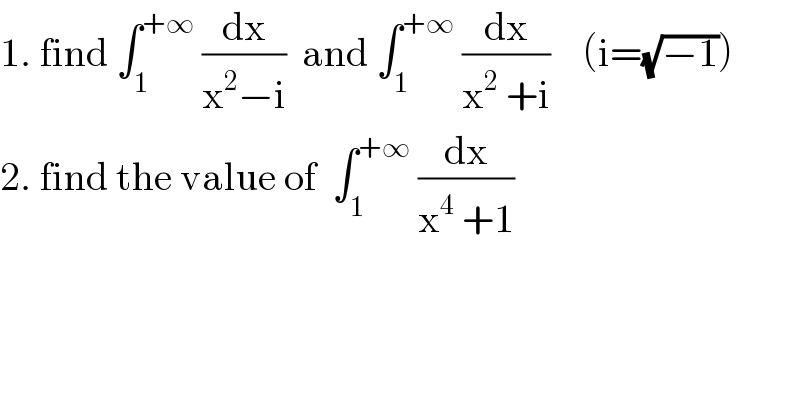
$$\mathrm{1}.\:\mathrm{find}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}\:\:\mathrm{and}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{i}}\:\:\:\:\left(\mathrm{i}=\sqrt{−\mathrm{1}}\right) \\ $$$$\mathrm{2}.\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{1}} \\ $$
Answered by Sourav mridha last updated on 01/Jun/20
![let I=∫_1 ^(+∞) (dx/(x^2 −i)) and J=∫_1 ^(+∞) (dx/(x^2 +i)) now, I+J=∫_1 ^(+∞) ((2x^2 )/(x^4 +1))dx.....(i) =∫_1 ^(+∞) ((x^2 +1)/(x^4 +1))dx +∫_1 ^∞ ((x^2 −1)/(x^4 +1))dx ........(I_1 ) ..........(I_2 ) =∫_(1 ) ^(+∞) ((d(x−(1/x)))/((x−(1/x))^2 +((√2))^2 )) +∫_1 ^(+∞) ((d(x+(1/x)))/((x+(1/x))^2 −((√2))^2 )) =(1/( (√2)))[tan^(−1) (((x−(1/x))/( (√2))))]_1 ^(+∞) +(1/(2(√2)))[ln(((x+(1/x) −(√2))/(x+(1/x)+(√2))))]_1 ^(+∞) =(𝛑/(2(√2)))−(1/(2(√2)))ln(3−(√2)) now I−J=(1/(2i))∫_1 ^(+∞) (dx/(x^4 +1)) ......(ii) =(1/(4i))[∫_1 ^(+∞) ((x^2 +1)/(x^4 +1))dx−∫_1 ^(+∞) ((x^2 −1)/(x^4 +1))dx] =(1/(4i))[I_1 −I_2 ]=−(i/4)[(𝛑/(2(√2)))+(1/(2(√2)))ln(3−(√2))] now (i)+(ii) I=[(𝛑/(4(√2)))−(1/(4(√2)))ln(3−(√2))]−i[(𝛑/(16(√2)))+(1/(16(√2)))ln(3−(√2))] and (i)−(ii) J=I^∗ =complex conjugate of I. now from (ii)... ∫_1 ^(+∞) (dx/(x^4 +1))=2i(I−J) =[(𝛑/(4(√2)))+(1/(4(√2)))ln(3−(√2))]. very nice problem...it′s really interesting.](https://www.tinkutara.com/question/Q96399.png)
$$\boldsymbol{{let}}\:\boldsymbol{{I}}=\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{dx}}}{\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{i}}}\:\boldsymbol{{and}}\:\boldsymbol{{J}}=\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{dx}}}{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{i}}}\: \\ $$$$\boldsymbol{{now}},\:\boldsymbol{{I}}+\mathrm{J}=\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{1}}\boldsymbol{{dx}}…..\left(\boldsymbol{{i}}\right) \\ $$$$\:\:\:\:=\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{1}}\boldsymbol{{dx}}\:+\int_{\mathrm{1}} ^{\infty} \frac{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{1}}\boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:……..\left(\boldsymbol{{I}}_{\mathrm{1}} \right)\:\:\:\:\:\:\:\:\:\:\:……….\left(\boldsymbol{{I}}_{\mathrm{2}} \right) \\ $$$$=\int_{\mathrm{1}\:} ^{+\infty} \frac{\boldsymbol{{d}}\left(\boldsymbol{{x}}−\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)}{\left(\boldsymbol{{x}}−\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\:+\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{d}}\left(\boldsymbol{{x}}+\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)}{\left(\boldsymbol{{x}}+\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\boldsymbol{{x}}−\frac{\mathrm{1}}{\boldsymbol{{x}}}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{1}} ^{+\infty} +\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\boldsymbol{{ln}}\left(\frac{\boldsymbol{{x}}+\frac{\mathrm{1}}{\boldsymbol{{x}}}\:−\sqrt{\mathrm{2}}}{\boldsymbol{{x}}+\frac{\mathrm{1}}{\boldsymbol{{x}}}+\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{1}} ^{+\infty} \\ $$$$=\frac{\boldsymbol{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\boldsymbol{{ln}}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right) \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{I}}−\boldsymbol{{J}}=\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{i}}}\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{dx}}}{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{1}}\:……\left(\boldsymbol{{ii}}\right) \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{4}\boldsymbol{{i}}}\left[\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{1}}\boldsymbol{{dx}}−\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{1}}\boldsymbol{{dx}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\boldsymbol{{i}}}\left[\boldsymbol{{I}}_{\mathrm{1}} −\boldsymbol{{I}}_{\mathrm{2}} \right]=−\frac{\boldsymbol{{i}}}{\mathrm{4}}\left[\frac{\boldsymbol{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\boldsymbol{{ln}}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)\right] \\ $$$$\boldsymbol{{now}}\:\left(\boldsymbol{{i}}\right)+\left(\boldsymbol{{ii}}\right) \\ $$$$\boldsymbol{{I}}=\left[\frac{\boldsymbol{\pi}}{\mathrm{4}\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\boldsymbol{{ln}}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)\right]−\boldsymbol{{i}}\left[\frac{\boldsymbol{\pi}}{\mathrm{16}\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}}}\boldsymbol{{ln}}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)\right] \\ $$$$\boldsymbol{{and}}\:\left(\boldsymbol{{i}}\right)−\left(\boldsymbol{{ii}}\right) \\ $$$$\boldsymbol{{J}}=\boldsymbol{{I}}^{\ast} =\boldsymbol{{complex}}\:\boldsymbol{{conjugate}}\:\boldsymbol{{of}}\:\boldsymbol{{I}}. \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{from}}\:\left(\boldsymbol{{ii}}\right)… \\ $$$$\:\:\int_{\mathrm{1}} ^{+\infty} \frac{\boldsymbol{{dx}}}{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{1}}=\mathrm{2}\boldsymbol{{i}}\left(\boldsymbol{{I}}−\boldsymbol{{J}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\frac{\boldsymbol{\pi}}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\boldsymbol{{ln}}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)\right]. \\ $$$$\boldsymbol{{very}}\:\boldsymbol{{nice}}\:\boldsymbol{{problem}}…\boldsymbol{{it}}'\mathrm{s}\:\boldsymbol{{really}} \\ $$$$\boldsymbol{{interesting}}. \\ $$$$ \\ $$
Commented by abdomathmax last updated on 01/Jun/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Answered by abdomathmax last updated on 01/Jun/20
![1. ∫_1 ^(+∞) (dx/(x^2 −i)) =∫_1 ^(+∞) (dx/((x−(√i))(x+(√i)))) =(1/(2(√i)))∫_1 ^(+∞) ((1/(x−(√i)))−(1/(x+(√i))))dx =(1/(2(√i)))[ln(((x−(√i))/(x+(√i))))]_1 ^(+∞) =(1/(2(√i)))(−ln(((1−(√i))/(1+(√i))))) =(1/(2(√i)))( ln(1+(√i))−ln(1−(√i))) but 1+(√i)=1+e^((iπ)/4) =1+(1/( (√2)))+(i/( (√2))) =(√((1+(1/( (√2))))^2 +(1/2)))× e^(iarctan((1/( (√2)(1+(1/( (√2))))))) =(√((3/2)+(√2)+(1/2)))e^(iarctan((1/(1+(√2))))) =(√(2+(√2))) e^(iarctan((1/(1+(√2))))) ⇒ ln(1+(√i))=(1/2)ln(2+(√2))+iarctan((1/(1+(√2)))) ln(1−(√i)) =conj(..)=(1/2)ln(2+(√2))−iarctan((1/(1+(√2)))) ⇒(1/(2(√i)))(ln(1+(√i))−ln(1−(√i))) =(1/(2(√i))){2i arctan((1/(1+(√2))))} =(√i)arctan((√2)−1) =(√i)((π/8)) =(π/8)e^((iπ)/4) ∫_1 ^(+∞) (dx/(x^2 +i)) =conj(∫_1 ^(+∞) (dx/(x^2 −i))) =(π/8)e^(−((iπ)/4)) 2.∫_1 ^(+∞) (dx/(x^4 +1)) =∫_1 ^(+∞) (dx/((x^2 −i)(x^2 +i))) =(1/(2i))∫_1 ^(+∞) ((1/(x^2 −i))−(1/(x^2 +i)))dx =(1/(2i))((π/8)e^((iπ)/4) −(π/8)e^(−((iπ)/4)) ) =(π/8)sin((π/4)) =(π/8)×((√2)/2) =((π(√2))/(16))](https://www.tinkutara.com/question/Q96434.png)
$$\mathrm{1}.\:\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}−\sqrt{\mathrm{i}}\right)\left(\mathrm{x}+\sqrt{\mathrm{i}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\int_{\mathrm{1}} ^{+\infty} \:\left(\frac{\mathrm{1}}{\mathrm{x}−\sqrt{\mathrm{i}}}−\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{i}}}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\left[\mathrm{ln}\left(\frac{\mathrm{x}−\sqrt{\mathrm{i}}}{\mathrm{x}+\sqrt{\mathrm{i}}}\right)\right]_{\mathrm{1}} ^{+\infty} \:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\left(−\mathrm{ln}\left(\frac{\mathrm{1}−\sqrt{\mathrm{i}}}{\mathrm{1}+\sqrt{\mathrm{i}}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\left(\:\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{i}}\right)−\mathrm{ln}\left(\mathrm{1}−\sqrt{\mathrm{i}}\right)\right)\:\:\mathrm{but} \\ $$$$\mathrm{1}+\sqrt{\mathrm{i}}=\mathrm{1}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\:=\sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}}× \\ $$$$\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right.}\right)} \:=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}+\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)} \\ $$$$=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\:\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)} \:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{i}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right) \\ $$$$\mathrm{ln}\left(\mathrm{1}−\sqrt{\mathrm{i}}\right)\:=\mathrm{conj}\left(..\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)−\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\left(\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{i}}\right)−\mathrm{ln}\left(\mathrm{1}−\sqrt{\mathrm{i}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\left\{\mathrm{2i}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)\right\}\:=\sqrt{\mathrm{i}}\mathrm{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$=\sqrt{\mathrm{i}}\left(\frac{\pi}{\mathrm{8}}\right)\:=\frac{\pi}{\mathrm{8}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{i}}\:=\mathrm{conj}\left(\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}\right)\:=\frac{\pi}{\mathrm{8}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$\mathrm{2}.\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{1}}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{i}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\int_{\mathrm{1}} ^{+\infty} \:\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{i}}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\left(\frac{\pi}{\mathrm{8}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} −\frac{\pi}{\mathrm{8}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\: \\ $$$$=\frac{\pi}{\mathrm{8}}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)\:=\frac{\pi}{\mathrm{8}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$$$ \\ $$
