Question Number 40008 by math khazana by abdo last updated on 15/Jul/18
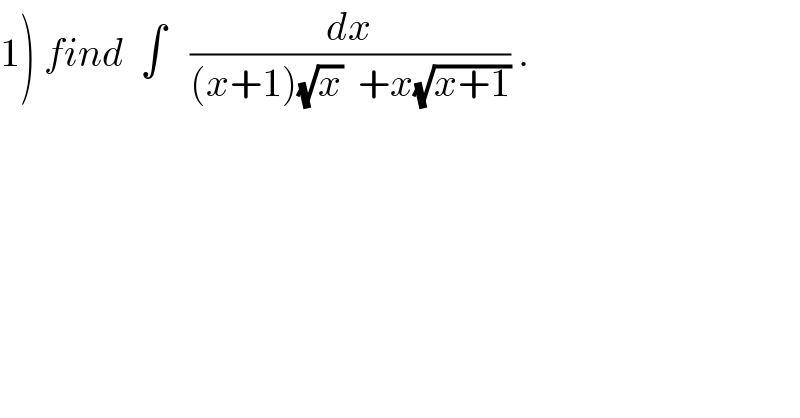
$$\left.\mathrm{1}\right)\:{find}\:\:\int\:\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}}\:\:+{x}\sqrt{{x}+\mathrm{1}}}\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 15/Jul/18
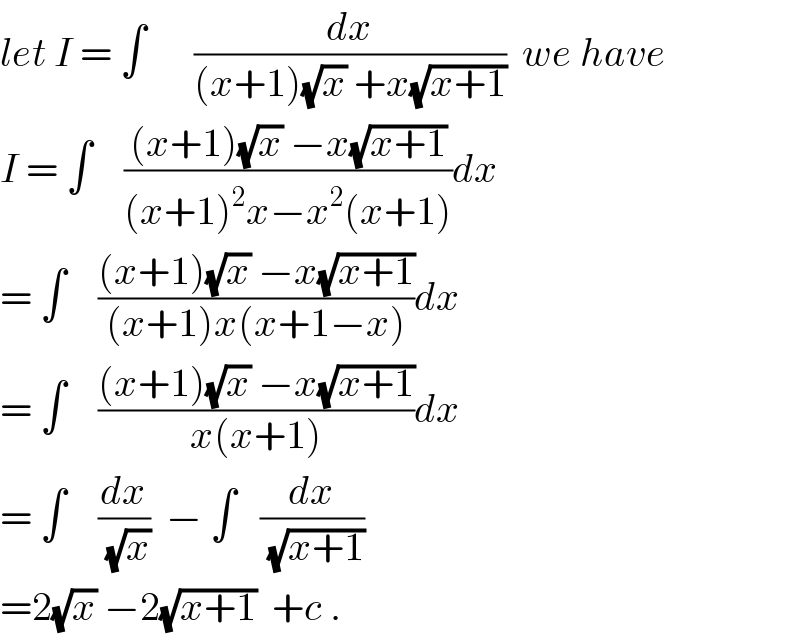
$${let}\:{I}\:=\:\int\:\:\:\:\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}}\:+{x}\sqrt{{x}+\mathrm{1}}}\:\:{we}\:{have}\: \\ $$$${I}\:=\:\int\:\:\:\:\frac{\left({x}+\mathrm{1}\right)\sqrt{{x}}\:−{x}\sqrt{{x}+\mathrm{1}}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} {x}−{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx} \\ $$$$=\:\int\:\:\:\:\frac{\left({x}+\mathrm{1}\right)\sqrt{{x}}\:−{x}\sqrt{{x}+\mathrm{1}}}{\left({x}+\mathrm{1}\right){x}\left({x}+\mathrm{1}−{x}\right)}{dx} \\ $$$$=\:\int\:\:\:\:\frac{\left({x}+\mathrm{1}\right)\sqrt{{x}}\:−{x}\sqrt{{x}+\mathrm{1}}}{{x}\left({x}+\mathrm{1}\right)}{dx} \\ $$$$=\:\int\:\:\:\:\frac{{dx}}{\:\sqrt{{x}}}\:\:−\:\int\:\:\:\frac{{dx}}{\:\sqrt{{x}+\mathrm{1}}} \\ $$$$=\mathrm{2}\sqrt{{x}}\:−\mathrm{2}\sqrt{{x}+\mathrm{1}}\:\:+{c}\:. \\ $$
Answered by ajfour last updated on 15/Jul/18
![I=∫(([(x+1)(√x)−x(√(x+1)) ]dx)/(x(x+1)[x+1−x])) =∫(dx/( (√x)))−∫(dx/( (√(x+1)))) =2(√x)−2(√(x+1))+c .](https://www.tinkutara.com/question/Q40011.png)
$${I}=\int\frac{\left[\left({x}+\mathrm{1}\right)\sqrt{{x}}−{x}\sqrt{{x}+\mathrm{1}}\:\right]{dx}}{{x}\left({x}+\mathrm{1}\right)\left[{x}+\mathrm{1}−{x}\right]} \\ $$$$\:\:\:=\int\frac{{dx}}{\:\sqrt{{x}}}−\int\frac{{dx}}{\:\sqrt{{x}+\mathrm{1}}} \\ $$$$\:\:\:=\mathrm{2}\sqrt{{x}}−\mathrm{2}\sqrt{{x}+\mathrm{1}}+{c}\:. \\ $$
