Menu Close

1-find-dx-x-2-1-9-2-calculate-2-dx-x-2-1-9-

Tinku Tara 0 Comments
Pin




Question Number 82970 by mathmax by abdo last updated on 26/Feb/20
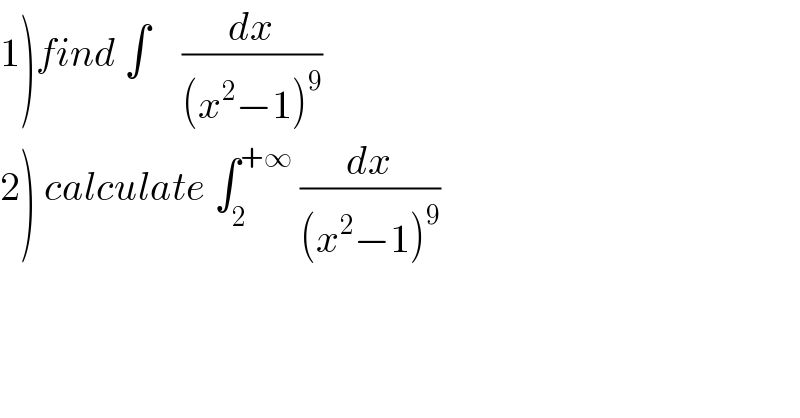
1)find ∫ (dx/((x^2 −1)^9 )) 2) calculate ∫_2 ^(+∞) (dx/((x^2 −1)^9 ))
$$\left.\mathrm{1}\right){find}\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{9}} } \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{2}} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{9}} } \\ $$
Commented by mathmax by abdo last updated on 26/Feb/20
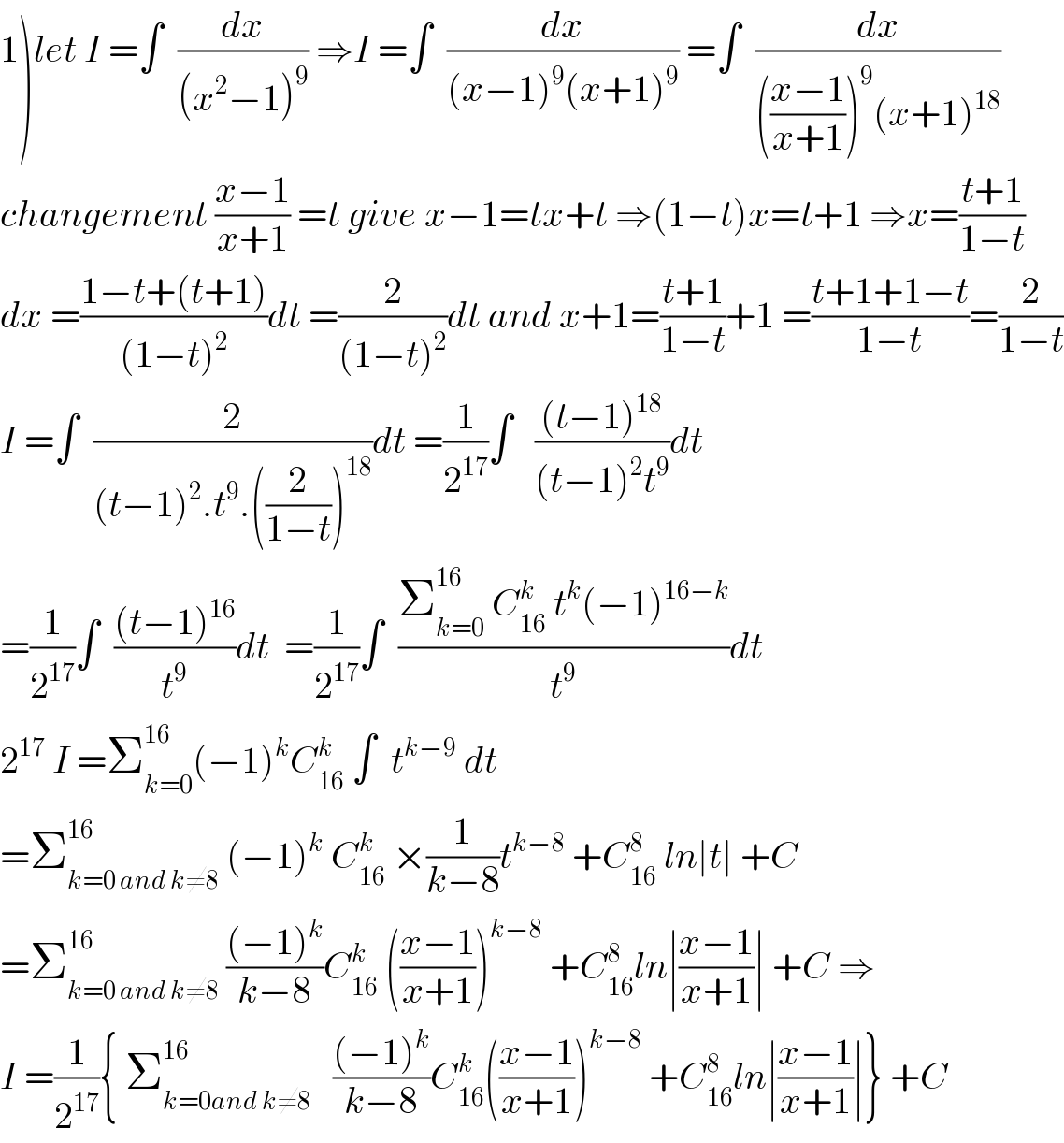
1)let I =∫ (dx/((x^2 −1)^9 )) ⇒I =∫ (dx/((x−1)^9 (x+1)^9 )) =∫ (dx/((((x−1)/(x+1)))^9 (x+1)^(18) )) changement ((x−1)/(x+1)) =t give x−1=tx+t ⇒(1−t)x=t+1 ⇒x=((t+1)/(1−t)) dx =((1−t+(t+1))/((1−t)^2 ))dt =(2/((1−t)^2 ))dt and x+1=((t+1)/(1−t))+1 =((t+1+1−t)/(1−t))=(2/(1−t)) I =∫ (2/((t−1)^2 .t^9 .((2/(1−t)))^(18) ))dt =(1/2^(17) )∫ (((t−1)^(18) )/((t−1)^2 t^9 ))dt =(1/2^(17) )∫ (((t−1)^(16) )/t^9 )dt =(1/2^(17) )∫ ((Σ_(k=0) ^(16) C_(16) ^k t^k (−1)^(16−k) )/t^9 )dt 2^(17) I =Σ_(k=0) ^(16) (−1)^k C_(16) ^k ∫ t^(k−9) dt =Σ_(k=0 and k≠8) ^(16) (−1)^k C_(16) ^k ×(1/(k−8))t^(k−8) +C_(16) ^8 ln∣t∣ +C =Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (((x−1)/(x+1)))^(k−8) +C_(16) ^8 ln∣((x−1)/(x+1))∣ +C ⇒ I =(1/2^(17) ){ Σ_(k=0and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (((x−1)/(x+1)))^(k−8) +C_(16) ^8 ln∣((x−1)/(x+1))∣} +C
$$\left.\mathrm{1}\right){let}\:{I}\:=\int\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{9}} }\:\Rightarrow{I}\:=\int\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{9}} \left({x}+\mathrm{1}\right)^{\mathrm{9}} }\:=\int\:\:\frac{{dx}}{\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{9}} \left({x}+\mathrm{1}\right)^{\mathrm{18}} } \\ $$$${changement}\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\:={t}\:{give}\:{x}−\mathrm{1}={tx}+{t}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}={t}+\mathrm{1}\:\Rightarrow{x}=\frac{{t}+\mathrm{1}}{\mathrm{1}−{t}} \\ $$$${dx}\:=\frac{\mathrm{1}−{t}+\left({t}+\mathrm{1}\right)}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt}\:=\frac{\mathrm{2}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt}\:{and}\:{x}+\mathrm{1}=\frac{{t}+\mathrm{1}}{\mathrm{1}−{t}}+\mathrm{1}\:=\frac{{t}+\mathrm{1}+\mathrm{1}−{t}}{\mathrm{1}−{t}}=\frac{\mathrm{2}}{\mathrm{1}−{t}} \\ $$$${I}\:=\int\:\:\frac{\mathrm{2}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} .{t}^{\mathrm{9}} .\left(\frac{\mathrm{2}}{\mathrm{1}−{t}}\right)^{\mathrm{18}} }{dt}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{17}} }\int\:\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{18}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{9}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{17}} }\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{16}} }{{t}^{\mathrm{9}} }{dt}\:\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{17}} }\int\:\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{16}} \:{C}_{\mathrm{16}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{16}−{k}} }{{t}^{\mathrm{9}} }{dt} \\ $$$$\mathrm{2}^{\mathrm{17}} \:{I}\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{16}} \left(−\mathrm{1}\right)^{{k}} {C}_{\mathrm{16}} ^{{k}} \:\int\:\:{t}^{{k}−\mathrm{9}} \:{dt} \\ $$$$=\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{8}} ^{\mathrm{16}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{16}} ^{{k}} \:×\frac{\mathrm{1}}{{k}−\mathrm{8}}{t}^{{k}−\mathrm{8}} \:+{C}_{\mathrm{16}} ^{\mathrm{8}} \:{ln}\mid{t}\mid\:+{C} \\ $$$$=\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{8}} ^{\mathrm{16}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{8}}{C}_{\mathrm{16}} ^{{k}} \:\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{{k}−\mathrm{8}} \:+{C}_{\mathrm{16}} ^{\mathrm{8}} {ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid\:+{C}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{17}} }\left\{\:\sum_{{k}=\mathrm{0}{and}\:{k}\neq\mathrm{8}} ^{\mathrm{16}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{8}}{C}_{\mathrm{16}} ^{{k}} \left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{{k}−\mathrm{8}} \:+{C}_{\mathrm{16}} ^{\mathrm{8}} {ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid\right\}\:+{C} \\ $$
Commented by mathmax by abdo last updated on 26/Feb/20
2) ∫_2 ^(+∞) (dx/((x^2 −1)^9 ))=(1/2^(17) )[Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (((x−1)/(x+1)))^(k−8) +C_(16) ^8 ln∣((x−1)/(x+1))∣]_2 ^(+∞) =(1/2^(17) ){Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k −Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k ((1/3))^(k−8) −C_(16) ^8 ln((1/3))} =(1/2^(17) )Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (1−(1/3^(k−8) ))+(C_(16) ^8 /2^(17) )ln(3)
$$\left.\mathrm{2}\right)\:\int_{\mathrm{2}} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{9}} }=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{17}} }\left[\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{8}} ^{\mathrm{16}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{8}}{C}_{\mathrm{16}} ^{{k}} \left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{{k}−\mathrm{8}} \:+{C}_{\mathrm{16}} ^{\mathrm{8}} {ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid\right]_{\mathrm{2}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{17}} }\left\{\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{8}} ^{\mathrm{16}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{8}}{C}_{\mathrm{16}} ^{{k}} \:−\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{8}} ^{\mathrm{16}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{8}}{C}_{\mathrm{16}} ^{{k}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{k}−\mathrm{8}} \right. \\ $$$$\left.−{C}_{\mathrm{16}} ^{\mathrm{8}} {ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{17}} }\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{8}} ^{\mathrm{16}} \frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{8}}{C}_{\mathrm{16}} ^{{k}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{{k}−\mathrm{8}} }\right)+\frac{{C}_{\mathrm{16}} ^{\mathrm{8}} }{\mathrm{2}^{\mathrm{17}} }{ln}\left(\mathrm{3}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *