Menu Close

1-find-dx-x-2-x-1-6-2-calculate-dx-x-2-x-1-6-

Tinku Tara 0 Comments
Pin




Question Number 82971 by mathmax by abdo last updated on 26/Feb/20
1)find ∫ (dx/((x^2 +x+1)^6 )) 2)calculate ∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^6 ))
$$\left.\mathrm{1}\right){find}\:\int\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{6}} } \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{6}} } \\ $$
Commented by mathmax by abdo last updated on 26/Feb/20
2) let A =∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^6 )) ⇒ A =∫_(−∞) ^(+∞) (dx/(((x+(1/2))^2 +(3/4))^6 )) =_(x+(1/2)=((√3)/2)t) ((4/3))^6 ∫_(−∞) ^(+∞) (dt/((t^2 +1)^6 )) let also changement t=tanθ give ∫_(−∞) ^(+∞) (dt/((t^2 +1)^6 )) =∫_(−(π/2)) ^(π/2) (((1+tan^2 θ)dθ)/((1+tan^2 θ)^6 )) =∫_(−(π/2)) ^(π/2) (dθ/((1+tan^2 θ)^4 )) =∫_(−(π/2)) ^(π/2) cos^8 t dt =2 ∫_0 ^(π/2) (((1+cos(2t))/2))^4 dt =(1/8)∫_0 ^(π/2) (1+2cos(2t) +cos^2 (2t))^2 dt =(1/8)∫_0 ^(π/2) { (1+2cos(2t))^2 +2(1+2cos(2t)cos^2 (2t) +cos^4 (2t))dt =(1/8)∫_0 ^(π/2) {1+4cos(2t) +4cos^2 (2t) +2cos^2 (2t)+4cos^3 (2t)+cos^4 (2t)}dt =(π/(16)) +(1/2)∫_0 ^(π/2) cos(2t)+(3/4)∫_0 ^(π/2) cos^2 (2t)dt+(1/2)∫_0 ^(π/2) cos^3 (2t)dt+(1/8)∫_0 ^(π/2) cos^4 (2t)dt ∫_0 ^(π/2) cos(2t)dt =(1/2)sin(2t)]_0 ^(π/2) =0 ∫_0 ^(π/2) cos^2 (2t)dt =(1/2)∫_0 ^(π/2) (1+cos(4t))dt =(π/4) +(1/8)[sin(4t)]_0 ^(π/2) =(π/4) ∫_0 ^(π/2) cos^3 (2t)dt =∫_0 ^(π/2) (((1+cos(4t))/2))cos(2t)dt =(1/2)∫_0 ^(π/2) {cos(2t)+cos(2t)cos(4t)}dt =(1/2)∫_0 ^(π/2) cos(2t)dt +(1/4)∫_0 ^(π/2) (cos(2t)+cos(6t))dt=0 ∫_0 ^(π/2) cos^4 t dt =∫_0 ^(π/2) (((1+cos(2t))/2))^2 dt =(1/4)∫_0 ^(π/2) (1+2cos(2t) +cos^2 (2t))dt =(π/8) +(1/2)∫_0 ^(π/2) cos(2t)dt +(1/8)∫_0 ^(π/2) (1+cos(4t))dt =(π/8) +0+(π/(16)) =((3π)/(16)) the value of I is known
$$\left.\mathrm{2}\right)\:{let}\:{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{6}} }\:\Rightarrow\:{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left(\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{6}} } \\ $$$$=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{6}} \:\:\int_{−\infty} ^{+\infty} \:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{6}} }\:\:{let}\:\:{also}\:{changement} \\ $$$${t}={tan}\theta\:{give}\:\int_{−\infty} ^{+\infty} \:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{6}} }\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{6}} } \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{d}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{4}} }\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{8}} {t}\:{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)^{\mathrm{4}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{t}\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\right)^{\mathrm{2}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{\:\:\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{t}\right)\right)^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{t}\right){cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\:+{cos}^{\mathrm{4}} \left(\mathrm{2}{t}\right)\right){dt}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{\mathrm{1}+\mathrm{4}{cos}\left(\mathrm{2}{t}\right)\:+\mathrm{4}{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\:+\mathrm{2}{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)+\mathrm{4}{cos}^{\mathrm{3}} \left(\mathrm{2}{t}\right)+{cos}^{\mathrm{4}} \left(\mathrm{2}{t}\right)\right\}{dt} \\ $$$$=\frac{\pi}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{t}\right)+\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right){dt}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{3}} \left(\mathrm{2}{t}\right){dt}+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{4}} \left(\mathrm{2}{t}\right){dt} \\ $$$$\left.\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+{cos}\left(\mathrm{4}{t}\right)\right){dt} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left[{sin}\left(\mathrm{4}{t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{3}} \left(\mathrm{2}{t}\right){dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}+{cos}\left(\mathrm{4}{t}\right)}{\mathrm{2}}\right){cos}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{{cos}\left(\mathrm{2}{t}\right)+{cos}\left(\mathrm{2}{t}\right){cos}\left(\mathrm{4}{t}\right)\right\}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{t}\right){dt}\:\:+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cos}\left(\mathrm{2}{t}\right)+{cos}\left(\mathrm{6}{t}\right)\right){dt}=\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{4}} {t}\:{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)^{\mathrm{2}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{t}\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{t}\right){dt}\:+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+{cos}\left(\mathrm{4}{t}\right)\right){dt} \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\mathrm{0}+\frac{\pi}{\mathrm{16}}\:=\frac{\mathrm{3}\pi}{\mathrm{16}}\:\:{the}\:{value}\:{of}\:\:{I}\:{is}\:{known} \\ $$
Commented by abdomathmax last updated on 26/Feb/20
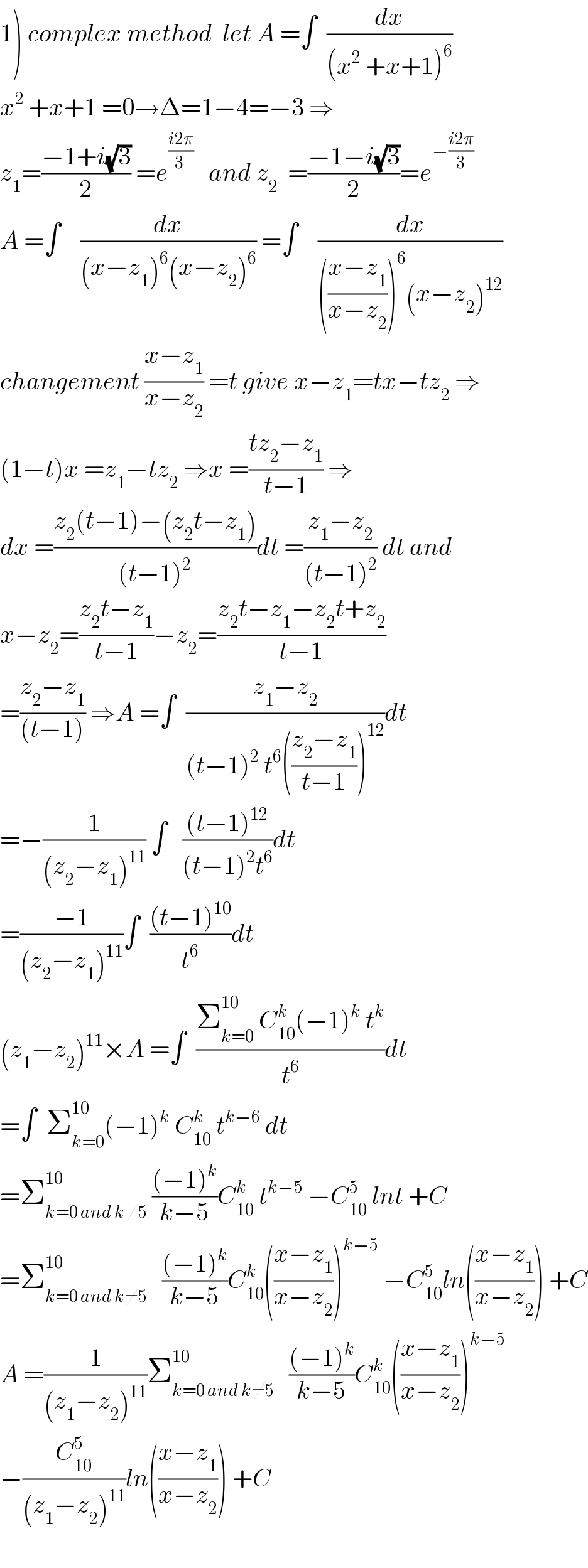
1) complex method let A =∫ (dx/((x^2 +x+1)^6 )) x^2 +x+1 =0→Δ=1−4=−3 ⇒ z_1 =((−1+i(√3))/2) =e^((i2π)/(3 )) and z_2 =((−1−i(√3))/2)=e^(−((i2π)/3)) A =∫ (dx/((x−z_1 )^6 (x−z_2 )^6 )) =∫ (dx/((((x−z_1 )/(x−z_2 )))^6 (x−z_2 )^(12) )) changement ((x−z_1 )/(x−z_2 )) =t give x−z_1 =tx−tz_2 ⇒ (1−t)x =z_1 −tz_2 ⇒x =((tz_2 −z_1 )/(t−1)) ⇒ dx =((z_2 (t−1)−(z_2 t−z_1 ))/((t−1)^2 ))dt =((z_1 −z_2 )/((t−1)^2 )) dt and x−z_2 =((z_2 t−z_1 )/(t−1))−z_2 =((z_2 t−z_1 −z_2 t+z_2 )/(t−1)) =((z_2 −z_1 )/((t−1))) ⇒A =∫ ((z_1 −z_2 )/((t−1)^2 t^6 (((z_2 −z_1 )/(t−1)))^(12) ))dt =−(1/((z_2 −z_1 )^(11) )) ∫ (((t−1)^(12) )/((t−1)^2 t^6 ))dt =((−1)/((z_2 −z_1 )^(11) ))∫ (((t−1)^(10) )/t^6 )dt (z_1 −z_2 )^(11) ×A =∫ ((Σ_(k=0) ^(10) C_(10) ^k (−1)^k t^k )/t^6 )dt =∫ Σ_(k=0) ^(10) (−1)^k C_(10) ^k t^(k−6) dt =Σ_(k=0 and k≠5) ^(10) (((−1)^k )/(k−5))C_(10) ^k t^(k−5) −C_(10) ^5 lnt +C =Σ_(k=0 and k≠5) ^(10) (((−1)^k )/(k−5))C_(10) ^k (((x−z_1 )/(x−z_2 )))^(k−5) −C_(10) ^5 ln(((x−z_1 )/(x−z_2 ))) +C A =(1/((z_1 −z_2 )^(11) ))Σ_(k=0 and k≠5) ^(10) (((−1)^k )/(k−5))C_(10) ^k (((x−z_1 )/(x−z_2 )))^(k−5) −(C_(10) ^5 /((z_1 −z_2 )^(11) ))ln(((x−z_1 )/(x−z_2 ))) +C
$$\left.\mathrm{1}\right)\:{complex}\:{method}\:\:{let}\:{A}\:=\int\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{6}} } \\ $$$${x}^{\mathrm{2}} \:+{x}+\mathrm{1}\:=\mathrm{0}\rightarrow\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}\:}} \:\:\:{and}\:{z}_{\mathrm{2}} \:\:=\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${A}\:=\int\:\:\:\:\frac{{dx}}{\left({x}−{z}_{\mathrm{1}} \right)^{\mathrm{6}} \left({x}−{z}_{\mathrm{2}} \right)^{\mathrm{6}} }\:=\int\:\:\:\:\frac{{dx}}{\left(\frac{{x}−{z}_{\mathrm{1}} }{{x}−{z}_{\mathrm{2}} }\right)^{\mathrm{6}} \left({x}−{z}_{\mathrm{2}} \right)^{\mathrm{12}} } \\ $$$${changement}\:\frac{{x}−{z}_{\mathrm{1}} }{{x}−{z}_{\mathrm{2}} }\:={t}\:{give}\:{x}−{z}_{\mathrm{1}} ={tx}−{tz}_{\mathrm{2}} \:\Rightarrow \\ $$$$\left(\mathrm{1}−{t}\right){x}\:={z}_{\mathrm{1}} −{tz}_{\mathrm{2}} \:\Rightarrow{x}\:=\frac{{tz}_{\mathrm{2}} −{z}_{\mathrm{1}} }{{t}−\mathrm{1}}\:\Rightarrow \\ $$$${dx}\:=\frac{{z}_{\mathrm{2}} \left({t}−\mathrm{1}\right)−\left({z}_{\mathrm{2}} {t}−{z}_{\mathrm{1}} \right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=\frac{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:{and} \\ $$$${x}−{z}_{\mathrm{2}} =\frac{{z}_{\mathrm{2}} {t}−{z}_{\mathrm{1}} }{{t}−\mathrm{1}}−{z}_{\mathrm{2}} =\frac{{z}_{\mathrm{2}} {t}−{z}_{\mathrm{1}} −{z}_{\mathrm{2}} {t}+{z}_{\mathrm{2}} }{{t}−\mathrm{1}} \\ $$$$=\frac{{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }{\left({t}−\mathrm{1}\right)}\:\Rightarrow{A}\:=\int\:\:\frac{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:{t}^{\mathrm{6}} \left(\frac{{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }{{t}−\mathrm{1}}\right)^{\mathrm{12}} }{dt} \\ $$$$=−\frac{\mathrm{1}}{\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)^{\mathrm{11}} }\:\int\:\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{12}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{6}} }{dt} \\ $$$$=\frac{−\mathrm{1}}{\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)^{\mathrm{11}} }\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{10}} }{{t}^{\mathrm{6}} }{dt} \\ $$$$\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{11}} ×{A}\:=\int\:\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{10}} \:{C}_{\mathrm{10}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} \:{t}^{{k}} }{{t}^{\mathrm{6}} }{dt} \\ $$$$=\int\:\:\sum_{{k}=\mathrm{0}} ^{\mathrm{10}} \left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{10}} ^{{k}} \:{t}^{{k}−\mathrm{6}} \:{dt} \\ $$$$=\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{5}} ^{\mathrm{10}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{5}}{C}_{\mathrm{10}} ^{{k}} \:{t}^{{k}−\mathrm{5}} \:−{C}_{\mathrm{10}} ^{\mathrm{5}} \:{lnt}\:+{C} \\ $$$$=\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{5}} ^{\mathrm{10}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{5}}{C}_{\mathrm{10}} ^{{k}} \left(\frac{{x}−{z}_{\mathrm{1}} }{{x}−{z}_{\mathrm{2}} }\right)^{{k}−\mathrm{5}} \:−{C}_{\mathrm{10}} ^{\mathrm{5}} {ln}\left(\frac{{x}−{z}_{\mathrm{1}} }{{x}−{z}_{\mathrm{2}} }\right)\:+{C} \\ $$$${A}\:=\frac{\mathrm{1}}{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{11}} }\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{5}} ^{\mathrm{10}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\mathrm{5}}{C}_{\mathrm{10}} ^{{k}} \left(\frac{{x}−{z}_{\mathrm{1}} }{{x}−{z}_{\mathrm{2}} }\right)^{{k}−\mathrm{5}} \\ $$$$−\frac{{C}_{\mathrm{10}} ^{\mathrm{5}} }{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{11}} }{ln}\left(\frac{{x}−{z}_{\mathrm{1}} }{{x}−{z}_{\mathrm{2}} }\right)\:+{C} \\ $$$$ \\ $$
Answered by MJS last updated on 26/Feb/20
Ostrogradski Q_1 (x)=(x^2 +x+1)^5 Q_2 (x)=x^2 +x+1 P_1 (x)=((28)/(27))(x+(1/2))(x^8 +4x^7 +((21)/6)x^6 +((35)/2)x^5 +((223)/(10))x^4 +((201)/(10))x^3 +((1973)/(140))x^2 +((881)/(140))x+((297)/(140))) P_2 (x)=((28)/(27)) ∫(dx/((x^2 +x+1)^6 ))=((P_1 (x))/(Q_1 (x)))+((28)/(27))∫(dx/(x^2 +x+1)) now it′s simplier than simple
$$\mathrm{Ostrogradski} \\ $$$${Q}_{\mathrm{1}} \left({x}\right)=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{5}} \\ $$$${Q}_{\mathrm{2}} \left({x}\right)={x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$$${P}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{28}}{\mathrm{27}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({x}^{\mathrm{8}} +\mathrm{4}{x}^{\mathrm{7}} +\frac{\mathrm{21}}{\mathrm{6}}{x}^{\mathrm{6}} +\frac{\mathrm{35}}{\mathrm{2}}{x}^{\mathrm{5}} +\frac{\mathrm{223}}{\mathrm{10}}{x}^{\mathrm{4}} +\frac{\mathrm{201}}{\mathrm{10}}{x}^{\mathrm{3}} +\frac{\mathrm{1973}}{\mathrm{140}}{x}^{\mathrm{2}} +\frac{\mathrm{881}}{\mathrm{140}}{x}+\frac{\mathrm{297}}{\mathrm{140}}\right) \\ $$$${P}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{28}}{\mathrm{27}} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{6}} }=\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}+\frac{\mathrm{28}}{\mathrm{27}}\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{simplier}\:\mathrm{than}\:\mathrm{simple} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *