1-Find-dy-dx-if-a-y-8x-1-x-2-4x-7-b-y-3x-4-10x-8-2x-2-5-2-Find-an-equation-of-the-tangen-line-to-the-graph-of-y-5-1-x-2-at-each-point-a-P-0-5-

Question Number 155857 by zainaltanjung last updated on 05/Oct/21

1) . Find \frac{dy}{dx}, if :

a) . y = (8 x - 1) (x^{2} + 4 x + 7)

b) . y = ({3 x}^{4} - 10 x + 8) ({2 x}^{2} + 5)

2) . Find an equation of the tangen line

to the graph of y = \frac{5}{1 + x^{2}} at each point

a) . P (0, 5) b) . Q (1, \frac{5}{2})

3) . Find the coordinat of all point on

the graph of : y = x^{3} + {2 x}^{2} - 4 x + 5 at which the

tangen line is :

a) . horizontal .

b) . paralel to the line

y = 2 y + 8 x - 5 = 0

4) . Find point P on the graph of y = x^{3}

such that the tangen line at P has

x - intercept 4

5) . Find the points at which the graph

f (x) and f^{^{'}} (x) is intersect, given that

a) . f (x) = x^{3} - x^{2} + x + 1

b) . f (x) = x^{2} + 2 x + 1

Answered by MathsFan last updated on 05/Oct/21

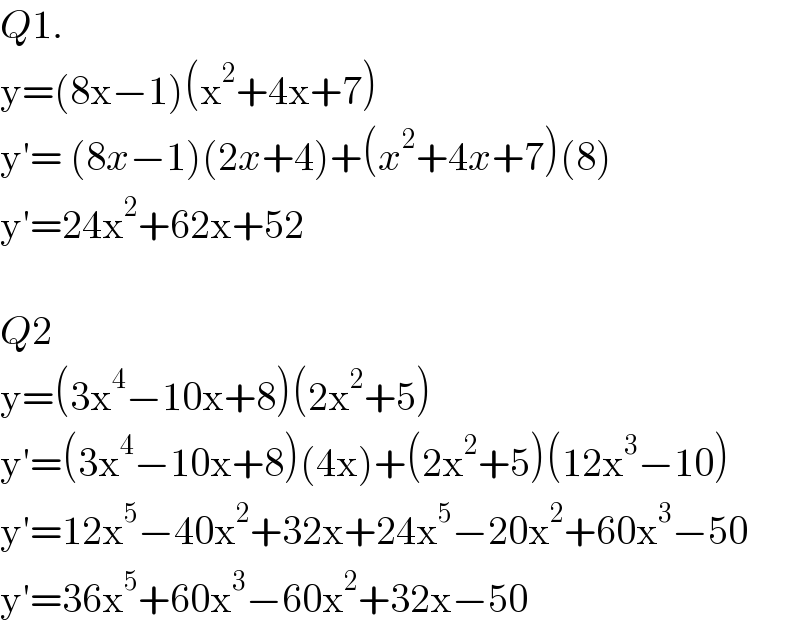
Q 1 .

y = (8 x - 1) (x^{2} + 4 x + 7)

y^{'} = (8 x - 1) (2 x + 4) + (x^{2} + 4 x + 7) (8)

y^{'} = {24 x}^{2} + 62 x + 52

Q 2

y = ({3 x}^{4} - 10 x + 8) ({2 x}^{2} + 5)

y^{'} = ({3 x}^{4} - 10 x + 8) (4 x) + ({2 x}^{2} + 5) ({12 x}^{3} - 10)

y^{'} = {12 x}^{5} - {40 x}^{2} + 32 x + {24 x}^{5} - {20 x}^{2} + {60 x}^{3} - 50

y^{'} = {36 x}^{5} + {60 x}^{3} - {60 x}^{2} + 32 x - 50

Commented by zainaltanjung last updated on 05/Oct/21

thanks sir