Question Number 118798 by WasimShaikh last updated on 19/Oct/20
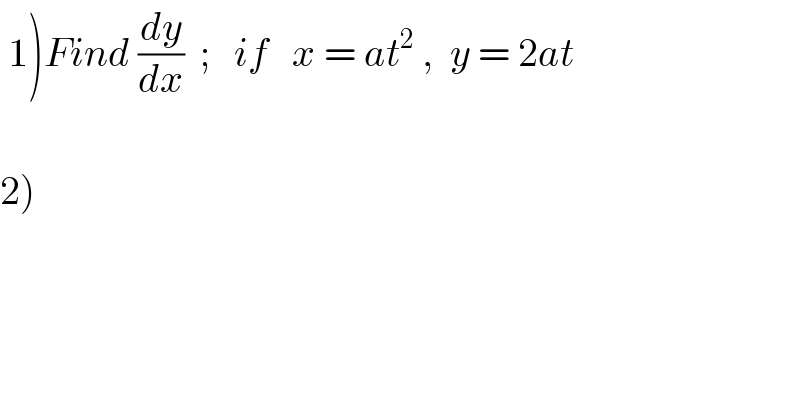
$$\left.\:\mathrm{1}\right){Find}\:\frac{{dy}}{{dx}}\:\:;\:\:\:{if}\:\:\:{x}\:=\:{at}^{\mathrm{2}} \:,\:\:{y}\:=\:\mathrm{2}{at} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\: \\ $$
Answered by Dwaipayan Shikari last updated on 20/Oct/20
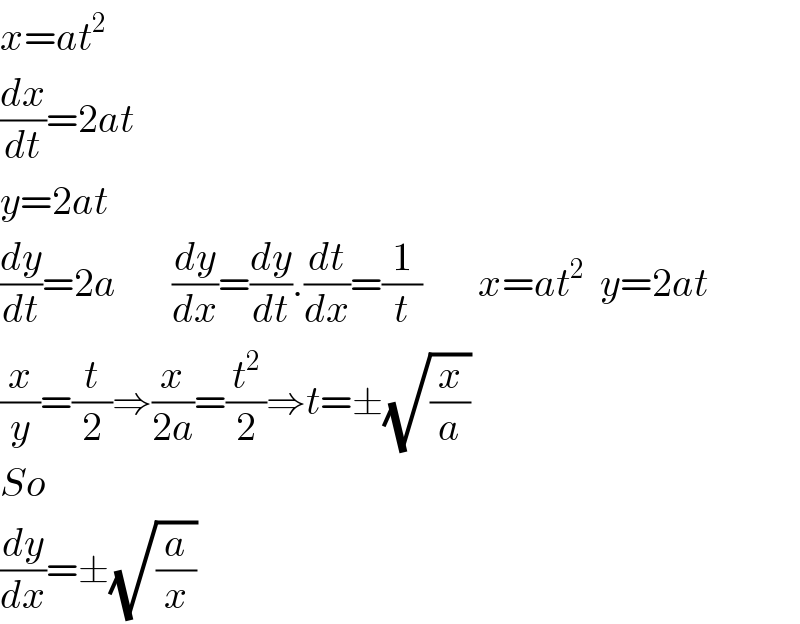
$${x}={at}^{\mathrm{2}} \\ $$$$\frac{{dx}}{{dt}}=\mathrm{2}{at} \\ $$$${y}=\mathrm{2}{at} \\ $$$$\frac{{dy}}{{dt}}=\mathrm{2}{a}\:\:\:\:\:\:\:\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}.\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{t}}\:\:\:\:\:\:\:{x}={at}^{\mathrm{2}} \:\:{y}=\mathrm{2}{at} \\ $$$$\frac{{x}}{{y}}=\frac{{t}}{\mathrm{2}}\Rightarrow\frac{{x}}{\mathrm{2}{a}}=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\Rightarrow{t}=\pm\sqrt{\frac{{x}}{{a}}} \\ $$$${So} \\ $$$$\frac{{dy}}{{dx}}=\pm\sqrt{\frac{{a}}{{x}}} \\ $$
Answered by Olaf last updated on 19/Oct/20
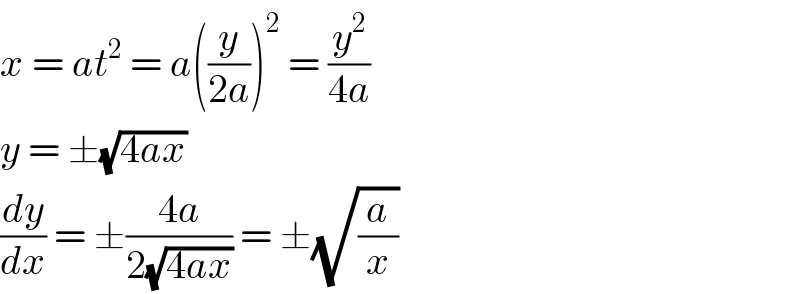
$${x}\:=\:{at}^{\mathrm{2}} \:=\:{a}\left(\frac{{y}}{\mathrm{2}{a}}\right)^{\mathrm{2}} \:=\:\frac{{y}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$${y}\:=\:\pm\sqrt{\mathrm{4}{ax}} \\ $$$$\frac{{dy}}{{dx}}\:=\:\pm\frac{\mathrm{4}{a}}{\mathrm{2}\sqrt{\mathrm{4}{ax}}}\:=\:\pm\sqrt{\frac{{a}}{{x}}} \\ $$
