Question Number 65286 by mathmax by abdo last updated on 27/Jul/19
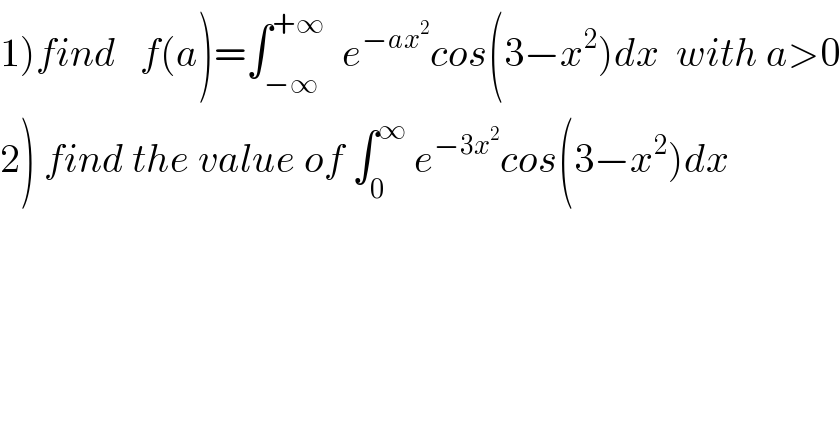
$$\left.\mathrm{1}\right){find}\:\:\:{f}\left({a}\right)=\int_{−\infty} ^{+\infty} \:\:{e}^{−{ax}^{\mathrm{2}} } {cos}\left(\mathrm{3}−{x}^{\mathrm{2}} \right){dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{3}{x}^{\mathrm{2}} } {cos}\left(\mathrm{3}−{x}^{\mathrm{2}} \right){dx} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 29/Jul/19

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:{e}^{−{ax}^{\mathrm{2}} } {cos}\left(\mathrm{3}−{x}^{\mathrm{2}} \right){dx}\:\Rightarrow \\ $$$${f}\left({a}\right)\:={Re}\left(\int_{−\infty} ^{+\infty} \:\:{e}^{−{ax}^{\mathrm{2}} +{i}\left(\mathrm{3}−{x}^{\mathrm{2}} \right)} {dx}\right) \\ $$$${I}=\int_{−\infty} ^{+\infty} \:{e}^{−{ax}^{\mathrm{2}} \:+{i}\left(\mathrm{3}−{x}^{\mathrm{2}} \right)} {dx}\:={e}^{\mathrm{3}{i}} \:\int_{−\infty} ^{+\infty} \:{e}^{−\left({a}+{i}\right){x}^{\mathrm{2}} } {dx}\:\:{changement}\:\sqrt{{a}+{i}}{x}={t} \\ $$$${give}\:{I}\:={e}^{\mathrm{3}{i}} \:\:\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{t}^{\mathrm{2}} } \:\frac{{dt}}{\:\sqrt{{a}+{i}}}\:=\frac{{e}^{\mathrm{3}{i}} }{\:\sqrt{{a}+{i}}}\:\sqrt{\pi} \\ $$$${a}+{i}\:=\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:\left\{\frac{{a}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\:+\frac{{i}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\right\}\:={r}\:{e}^{{i}\theta} \:\Rightarrow{r}\:=\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:\:{and}\:\theta\:={arctan}\left(\frac{\mathrm{1}}{{a}}\right) \\ $$$$\sqrt{{a}+{i}}=\sqrt{{r}}{e}^{\frac{{i}}{\mathrm{2}}\theta} \:=\left(\mathrm{1}+{a}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{a}}\right)} \:=^{\mathrm{4}} \sqrt{\mathrm{1}+{a}^{\mathrm{2}} }{e}^{\frac{{i}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−{arctana}\right)} \\ $$$$=^{\mathrm{4}} \sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:{e}^{\frac{{i}\pi}{\mathrm{4}}−\frac{{i}}{\mathrm{2}}{arctana}} \:\Rightarrow \\ $$$${I}\:=\sqrt{\pi}\:\:\frac{{e}^{\mathrm{3}{i}} }{\left(^{\mathrm{4}} \sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right){e}^{\frac{{i}\pi}{\mathrm{4}}−\frac{{i}}{\mathrm{2}}{arctan}\left({a}\right)} }\:=\frac{\sqrt{\pi}}{\left(^{\mathrm{4}} \sqrt{\left.\mathrm{1}+{a}^{\mathrm{2}} \right)}\right.}\:{e}^{\mathrm{3}{i}−\frac{{i}\pi}{\mathrm{4}}\:+\frac{{i}}{\mathrm{2}}{arctan}\left({a}\right)} \\ $$$$=\frac{\sqrt{\pi}}{\left(^{\mathrm{4}} \sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)}\:{e}^{{i}\left(\mathrm{3}−\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({a}\right)\right)} \:\Rightarrow \\ $$$${f}\left({a}\right)\:=\frac{\sqrt{\pi}}{\left(^{\mathrm{4}} \sqrt{\left.\mathrm{1}+{a}^{\mathrm{2}} \right)}\right.}\:{cos}\left(\mathrm{3}−\frac{\pi}{\mathrm{4}}+\frac{{arctana}}{\mathrm{2}}\right)\:. \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{3}{x}^{\mathrm{2}} } {cos}\left(\mathrm{3}−{x}^{\mathrm{2}} \right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:{e}^{−\mathrm{3}{x}^{\mathrm{2}} } {cos}\left(\mathrm{3}−{x}^{\mathrm{2}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{f}\left(\mathrm{3}\right)\:=\frac{\sqrt{\pi}}{\left(^{\mathrm{4}} \sqrt{\mathrm{10}}\right)}{cos}\left(\mathrm{3}−\frac{\pi}{\mathrm{4}}\:+\frac{{arctan}\left(\mathrm{3}\right)}{\mathrm{2}}\right) \\ $$
Commented by mathmax by abdo last updated on 29/Jul/19
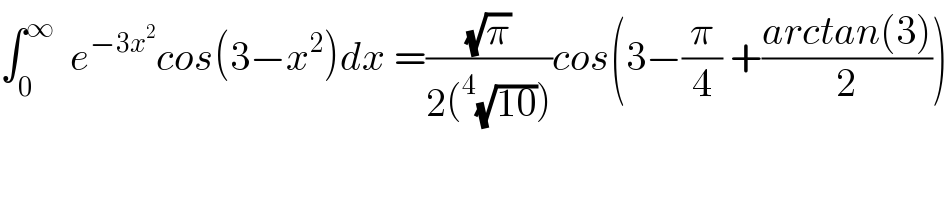
$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{3}{x}^{\mathrm{2}} } {cos}\left(\mathrm{3}−{x}^{\mathrm{2}} \right){dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}\left(^{\mathrm{4}} \sqrt{\mathrm{10}}\right)}{cos}\left(\mathrm{3}−\frac{\pi}{\mathrm{4}}\:+\frac{{arctan}\left(\mathrm{3}\right)}{\mathrm{2}}\right) \\ $$
