Menu Close

1-find-n-1-cos-nx-n-and-n-1-sin-nx-n-2-calculate-n-1-1-n-cos-2npi-3-and-n-1-1-n-sin-2npi-3-

Tinku Tara 0 Comments
Pin




Question Number 45968 by maxmathsup by imad last updated on 19/Oct/18
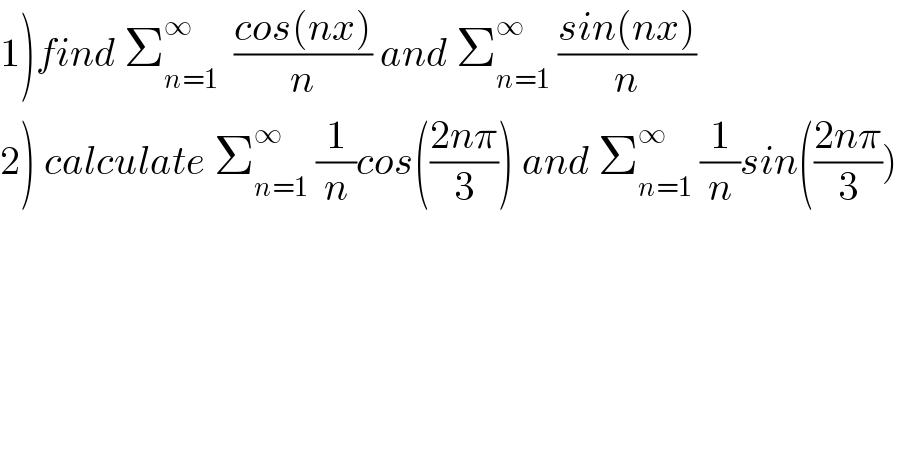
1)find Σ_(n=1) ^∞ ((cos(nx))/n) and Σ_(n=1) ^∞ ((sin(nx))/n) 2) calculate Σ_(n=1) ^∞ (1/n)cos(((2nπ)/3)) and Σ_(n=1) ^∞ (1/n)sin(((2nπ)/3))
$$\left.\mathrm{1}\right){find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{cos}\left({nx}\right)}{{n}}\:{and}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{n}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}{cos}\left(\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right)\:{and}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}{sin}\left(\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right) \\ $$
Commented by maxmathsup by imad last updated on 23/Oct/18
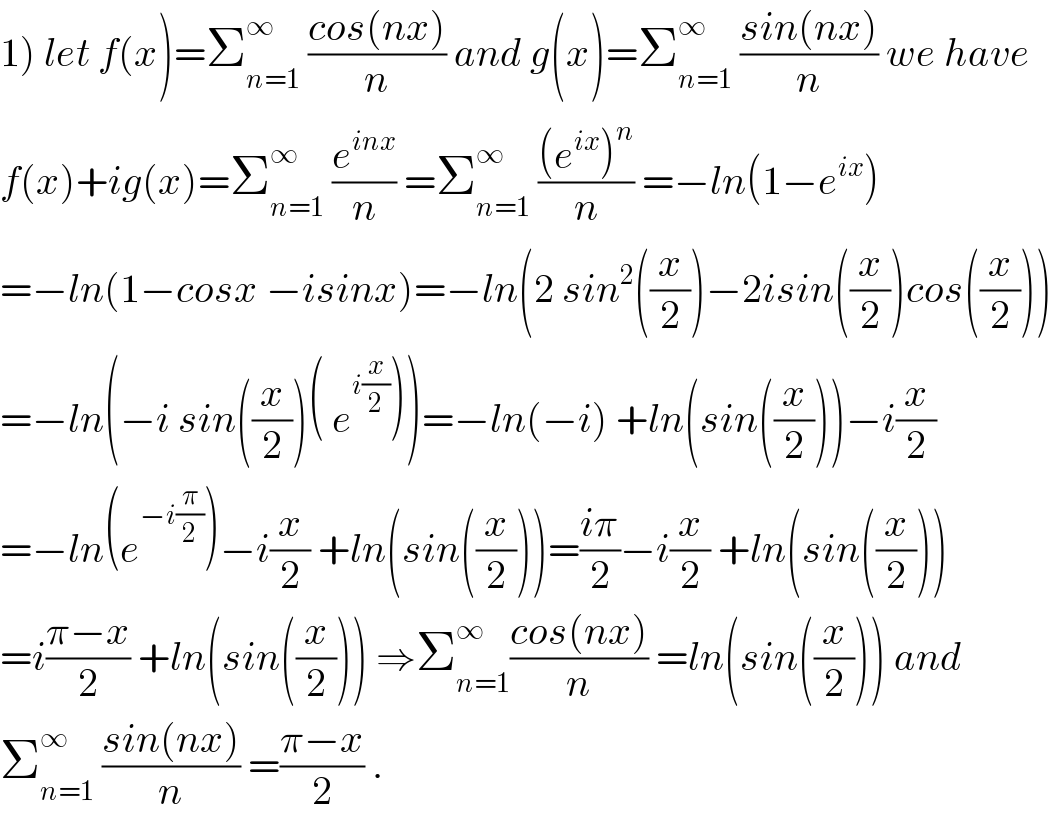
1) let f(x)=Σ_(n=1) ^∞ ((cos(nx))/n) and g(x)=Σ_(n=1) ^∞ ((sin(nx))/n) we have f(x)+ig(x)=Σ_(n=1) ^∞ (e^(inx) /n) =Σ_(n=1) ^∞ (((e^(ix) )^n )/n) =−ln(1−e^(ix) ) =−ln(1−cosx −isinx)=−ln(2 sin^2 ((x/2))−2isin((x/2))cos((x/2))) =−ln(−i sin((x/2))( e^(i(x/2)) ))=−ln(−i) +ln(sin((x/2)))−i(x/2) =−ln(e^(−i(π/2)) )−i(x/2) +ln(sin((x/2)))=((iπ)/2)−i(x/2) +ln(sin((x/2))) =i((π−x)/2) +ln(sin((x/2))) ⇒Σ_(n=1) ^∞ ((cos(nx))/n) =ln(sin((x/2))) and Σ_(n=1) ^∞ ((sin(nx))/n) =((π−x)/2) .
$$\left.\mathrm{1}\right)\:{let}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}}\:{and}\:{g}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{n}}\:{we}\:{have} \\ $$$${f}\left({x}\right)+{ig}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{inx}} }{{n}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left({e}^{{ix}} \right)^{{n}} }{{n}}\:=−{ln}\left(\mathrm{1}−{e}^{{ix}} \right) \\ $$$$=−{ln}\left(\mathrm{1}−{cosx}\:−{isinx}\right)=−{ln}\left(\mathrm{2}\:{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}{isin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$=−{ln}\left(−{i}\:{sin}\left(\frac{{x}}{\mathrm{2}}\right)\left(\:{e}^{{i}\frac{{x}}{\mathrm{2}}} \right)\right)=−{ln}\left(−{i}\right)\:+{ln}\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)\right)−{i}\frac{{x}}{\mathrm{2}} \\ $$$$=−{ln}\left({e}^{−{i}\frac{\pi}{\mathrm{2}}} \right)−{i}\frac{{x}}{\mathrm{2}}\:+{ln}\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)\right)=\frac{{i}\pi}{\mathrm{2}}−{i}\frac{{x}}{\mathrm{2}}\:+{ln}\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$={i}\frac{\pi−{x}}{\mathrm{2}}\:+{ln}\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)\right)\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{cos}\left({nx}\right)}{{n}}\:={ln}\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)\right)\:{and} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{n}}\:=\frac{\pi−{x}}{\mathrm{2}}\:. \\ $$
Commented by maxmathsup by imad last updated on 23/Oct/18
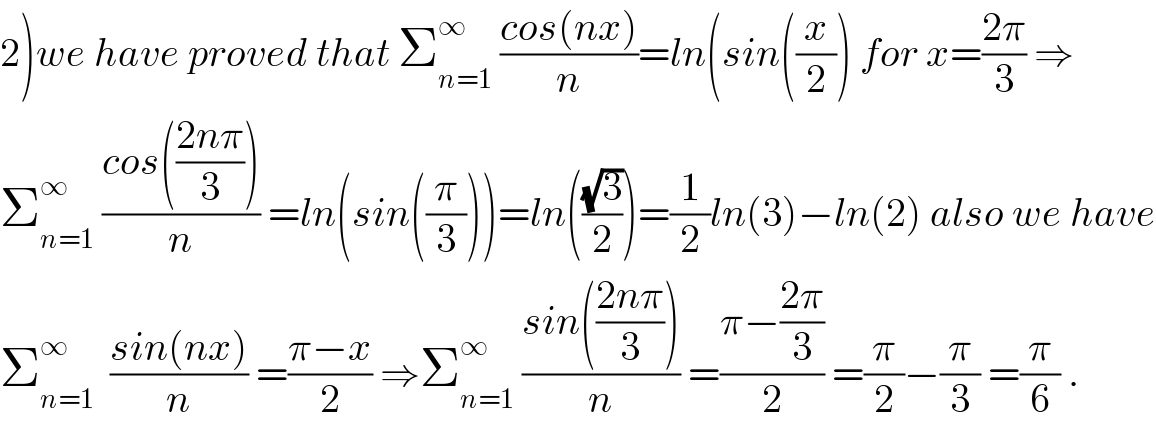
2)we have proved that Σ_(n=1) ^∞ ((cos(nx))/n)=ln(sin((x/2)) for x=((2π)/3) ⇒ Σ_(n=1) ^∞ ((cos(((2nπ)/3)))/n) =ln(sin((π/3)))=ln(((√3)/2))=(1/2)ln(3)−ln(2) also we have Σ_(n=1) ^∞ ((sin(nx))/n) =((π−x)/2) ⇒Σ_(n=1) ^∞ ((sin(((2nπ)/3)))/n) =((π−((2π)/3))/2) =(π/2)−(π/3) =(π/6) .
$$\left.\mathrm{2}\right){we}\:{have}\:{proved}\:{that}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}}={ln}\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)\:{for}\:{x}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:\Rightarrow\right. \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left(\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right)}{{n}}\:={ln}\left({sin}\left(\frac{\pi}{\mathrm{3}}\right)\right)={ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)−{ln}\left(\mathrm{2}\right)\:{also}\:{we}\:{have} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{sin}\left({nx}\right)}{{n}}\:=\frac{\pi−{x}}{\mathrm{2}}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left(\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right)}{{n}}\:=\frac{\pi−\frac{\mathrm{2}\pi}{\mathrm{3}}}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\:=\frac{\pi}{\mathrm{6}}\:. \\ $$
Answered by Smail last updated on 22/Oct/18
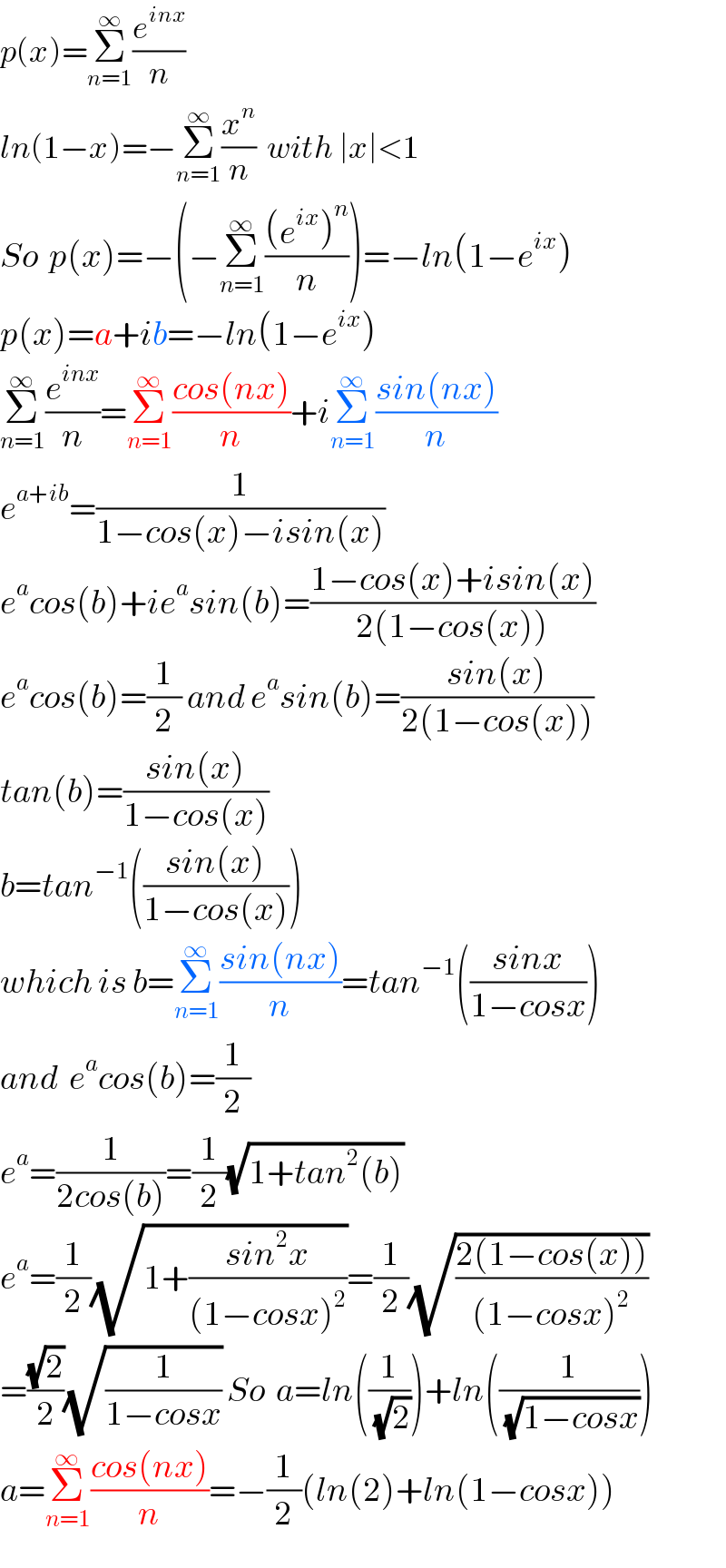
p(x)=Σ_(n=1) ^∞ (e^(inx) /n) ln(1−x)=−Σ_(n=1) ^∞ (x^n /n) with ∣x∣<1 So p(x)=−(−Σ_(n=1) ^∞ (((e^(ix) )^n )/n))=−ln(1−e^(ix) ) p(x)=a+ib=−ln(1−e^(ix) ) Σ_(n=1) ^∞ (e^(inx) /n)=Σ_(n=1) ^∞ ((cos(nx))/n)+iΣ_(n=1) ^∞ ((sin(nx))/n) e^(a+ib) =(1/(1−cos(x)−isin(x))) e^a cos(b)+ie^a sin(b)=((1−cos(x)+isin(x))/(2(1−cos(x)))) e^a cos(b)=(1/2) and e^a sin(b)=((sin(x))/(2(1−cos(x)))) tan(b)=((sin(x))/(1−cos(x))) b=tan^(−1) (((sin(x))/(1−cos(x)))) which is b=Σ_(n=1) ^∞ ((sin(nx))/n)=tan^(−1) (((sinx)/(1−cosx))) and e^a cos(b)=(1/2) e^a =(1/(2cos(b)))=(1/2)(√(1+tan^2 (b))) e^a =(1/2)(√(1+((sin^2 x)/((1−cosx)^2 ))))=(1/2)(√((2(1−cos(x)))/((1−cosx)^2 ))) =((√2)/2)(√(1/(1−cosx))) So a=ln((1/( (√2))))+ln((1/( (√(1−cosx))))) a=Σ_(n=1) ^∞ ((cos(nx))/n)=−(1/2)(ln(2)+ln(1−cosx))
$${p}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{inx}} }{{n}} \\ $$$${ln}\left(\mathrm{1}−{x}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}\:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$${So}\:\:{p}\left({x}\right)=−\left(−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({e}^{{ix}} \right)^{{n}} }{{n}}\right)=−{ln}\left(\mathrm{1}−{e}^{{ix}} \right) \\ $$$${p}\left({x}\right)={a}+{ib}=−{ln}\left(\mathrm{1}−{e}^{{ix}} \right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{inx}} }{{n}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left({nx}\right)}{{n}}+{i}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left({nx}\right)}{{n}} \\ $$$${e}^{{a}+{ib}} =\frac{\mathrm{1}}{\mathrm{1}−{cos}\left({x}\right)−{isin}\left({x}\right)} \\ $$$${e}^{{a}} {cos}\left({b}\right)+{ie}^{{a}} {sin}\left({b}\right)=\frac{\mathrm{1}−{cos}\left({x}\right)+{isin}\left({x}\right)}{\mathrm{2}\left(\mathrm{1}−{cos}\left({x}\right)\right)} \\ $$$${e}^{{a}} {cos}\left({b}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{e}^{{a}} {sin}\left({b}\right)=\frac{{sin}\left({x}\right)}{\mathrm{2}\left(\mathrm{1}−{cos}\left({x}\right)\right)} \\ $$$${tan}\left({b}\right)=\frac{{sin}\left({x}\right)}{\mathrm{1}−{cos}\left({x}\right)} \\ $$$${b}={tan}^{−\mathrm{1}} \left(\frac{{sin}\left({x}\right)}{\mathrm{1}−{cos}\left({x}\right)}\right) \\ $$$${which}\:{is}\:{b}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left({nx}\right)}{{n}}={tan}^{−\mathrm{1}} \left(\frac{{sinx}}{\mathrm{1}−{cosx}}\right) \\ $$$${and}\:\:{e}^{{a}} {cos}\left({b}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${e}^{{a}} =\frac{\mathrm{1}}{\mathrm{2}{cos}\left({b}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \left({b}\right)} \\ $$$${e}^{{a}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\frac{{sin}^{\mathrm{2}} {x}}{\left(\mathrm{1}−{cosx}\right)^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{2}\left(\mathrm{1}−{cos}\left({x}\right)\right)}{\left(\mathrm{1}−{cosx}\right)^{\mathrm{2}} }} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{1}−{cosx}}}\:{So}\:\:{a}={ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{cosx}}}\right) \\ $$$${a}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left({nx}\right)}{{n}}=−\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}−{cosx}\right)\right) \\ $$
Commented by Smail last updated on 22/Oct/18
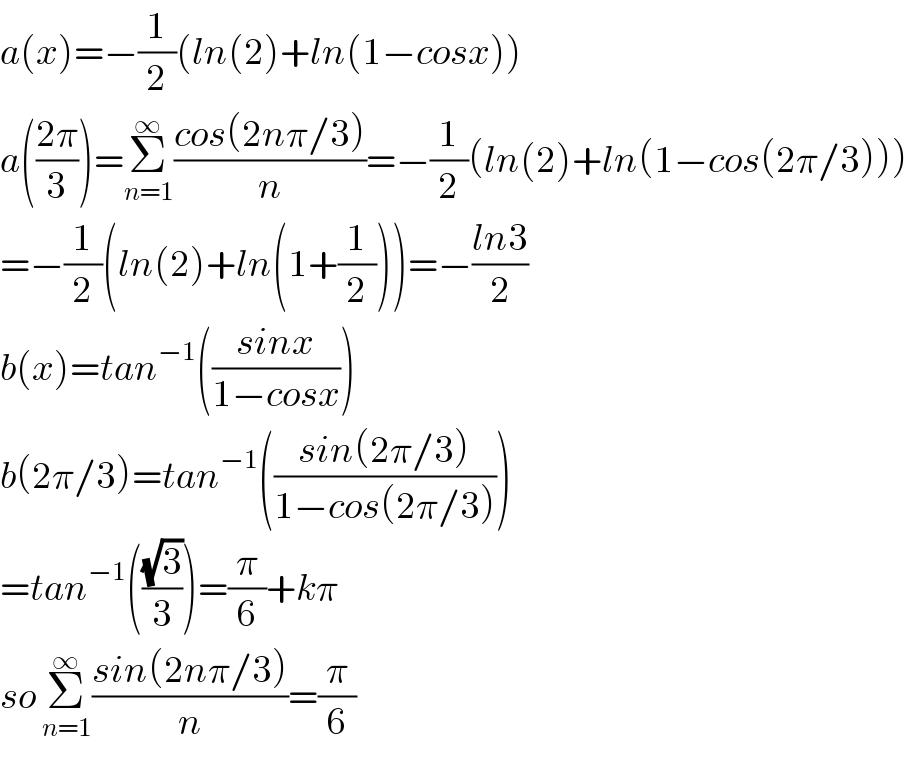
a(x)=−(1/2)(ln(2)+ln(1−cosx)) a(((2π)/3))=Σ_(n=1) ^∞ ((cos(2nπ/3))/n)=−(1/2)(ln(2)+ln(1−cos(2π/3))) =−(1/2)(ln(2)+ln(1+(1/2)))=−((ln3)/2) b(x)=tan^(−1) (((sinx)/(1−cosx))) b(2π/3)=tan^(−1) (((sin(2π/3))/(1−cos(2π/3)))) =tan^(−1) (((√3)/3))=(π/6)+kπ so Σ_(n=1) ^∞ ((sin(2nπ/3))/n)=(π/6)
$${a}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}−{cosx}\right)\right) \\ $$$${a}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left(\mathrm{2}{n}\pi/\mathrm{3}\right)}{{n}}=−\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}−{cos}\left(\mathrm{2}\pi/\mathrm{3}\right)\right)\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=−\frac{{ln}\mathrm{3}}{\mathrm{2}} \\ $$$${b}\left({x}\right)={tan}^{−\mathrm{1}} \left(\frac{{sinx}}{\mathrm{1}−{cosx}}\right) \\ $$$${b}\left(\mathrm{2}\pi/\mathrm{3}\right)={tan}^{−\mathrm{1}} \left(\frac{{sin}\left(\mathrm{2}\pi/\mathrm{3}\right)}{\mathrm{1}−{cos}\left(\mathrm{2}\pi/\mathrm{3}\right)}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)=\frac{\pi}{\mathrm{6}}+{k}\pi \\ $$$${so}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\mathrm{2}{n}\pi/\mathrm{3}\right)}{{n}}=\frac{\pi}{\mathrm{6}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *