Menu Close

1-find-the-radius-of-convergence-for-n-1-x-n-n-n-1-n-2-and-calculate-its-sum-2-find-the-value-of-n-1-1-n-n-2-n-n-1-n-2-

Tinku Tara 0 Comments
Pin




Question Number 33710 by math khazana by abdo last updated on 22/Apr/18
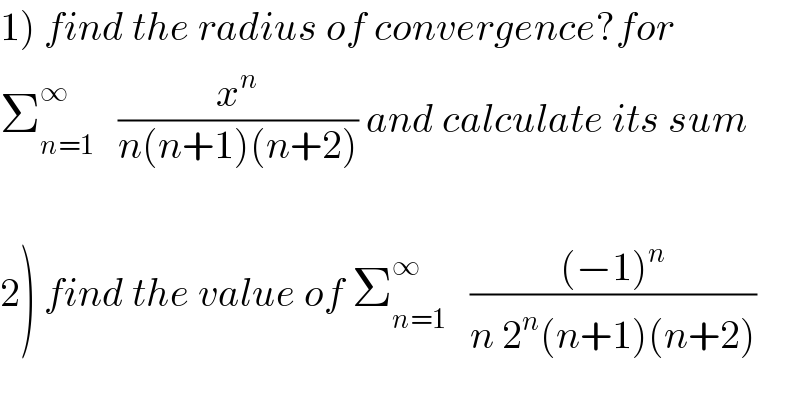
1) find the radius of convergence?for Σ_(n=1) ^∞ (x^n /(n(n+1)(n+2))) and calculate its sum 2) find the value of Σ_(n=1) ^∞ (((−1)^n )/(n 2^n (n+1)(n+2)))
$$\left.\mathrm{1}\right)\:{find}\:{the}\:{radius}\:{of}\:{convergence}?{for} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{x}^{{n}} }{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:{and}\:{calculate}\:{its}\:{sum} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\:\mathrm{2}^{{n}} \left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$
Commented by prof Abdo imad last updated on 27/Apr/18
let put u_n =(1/(n(n+1)(n+2))) we have (u_(n+1) /u_n ) = ((n(n+1)(n+2))/((n+1)(n+2)(n+3))) ⇒lim_(n→+∞) (u_(n+1) /u_n ) =1 ⇒ R =1 let decompose F(x)=(1/(x(x+1)(x+2))) F(x)= (a/x) +(b/(x+1))+(c/(x+2)) a=lim_(x→0) xF(x)=(1/2) b=lim_(x→−1) (x+1)F(x)= (1/(−1)) =−1 c=lim_(x→−2) (x+2)F(x)= (1/((−2)(−1))) =(1/2) ⇒ F(x)= (1/(2x)) −(1/(x+1)) + (1/(2(x+2))) S(x) =Σ_(n=1) ^∞ ((1/(2n)) −(1/(n+1)) +(1/(2(n+2))))x^n =(1/2) Σ_(n=1) ^∞ (x^n /n) −Σ_(n=1) ^∞ (x^n /(n+1)) +(1/2) Σ_(n=1) ^∞ (x^n /(n+2)) but Σ_(n=1) ^∞ (x^n /n) =−ln∣1−x∣ Σ_(n=1) ^∞ (x^n /(n+1)) =Σ_(n=2) ^(+∞) (x^(n−1) /n) = (1/x)( Σ_(n=2) ^(+∞) (x^n /n)) =(1/x)(−ln∣1−x∣−x) Σ_(n=1) ^∞ (x^n /(n+2)) = Σ_(n=3) ^(+∞) (x^(n−2) /n) =(1/x^2 ) Σ_(n=3) ^(+∞) (x^n /n) =(1/x^2 )( Σ_(n=1) ^∞ (x^n /n) −x −(x^2 /2)) = −((ln∣1−x∣)/x^2 ) −(1/x) −(1/2) ⇒ S(x)=−(1/2)ln∣1−x∣ −(1/x)(−ln∣1−x∣ −x) −((ln∣1−x∣)/(2x^2 )) −(1/(2x)) −(1/4) S(x)=(−(1/2) +(1/x) −(1/(2x^2 )))ln∣1−x∣ +1−(1/(2x)) −(1/4) S(x)=(−(1/2)+(1/x) −(1/(2x^2 )))ln∣1−x∣ −(1/(2x)) +(3/4) . 2) Σ_(n=1) ^∞ (((−1)^n )/(2^n n(n+1)(n+2))) = S(−(1/2)) =(−(1/2) −2 −2)ln((3/2)) +1 +(3/4) =(−(1/2)−4)ln((3/2)) +(7/4) = (7/4) −(9/2) (ln(3) −ln(2)) .
$${let}\:{put}\:{u}_{{n}} =\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:\:{we}\:{have} \\ $$$$\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }\:=\:\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }\:=\mathrm{1} \\ $$$$\Rightarrow\:{R}\:=\mathrm{1}\:\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)} \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{{b}}{{x}+\mathrm{1}}+\frac{{c}}{{x}+\mathrm{2}} \\ $$$${a}={lim}_{{x}\rightarrow\mathrm{0}} {xF}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${b}={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{−\mathrm{1}}\:=−\mathrm{1} \\ $$$${c}={lim}_{{x}\rightarrow−\mathrm{2}} \left({x}+\mathrm{2}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{\left(−\mathrm{2}\right)\left(−\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{x}}\:−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{2}\right)} \\ $$$${S}\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{2}\right)}\right){x}^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}+\mathrm{2}}\:{but} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:=−{ln}\mid\mathrm{1}−{x}\mid \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{x}^{{n}} }{{n}+\mathrm{1}}\:=\sum_{{n}=\mathrm{2}} ^{+\infty} \:\:\frac{{x}^{{n}−\mathrm{1}} }{{n}}\:=\:\frac{\mathrm{1}}{{x}}\left(\:\sum_{{n}=\mathrm{2}} ^{+\infty} \:\:\frac{{x}^{{n}} }{{n}}\right) \\ $$$$=\frac{\mathrm{1}}{{x}}\left(−{ln}\mid\mathrm{1}−{x}\mid−{x}\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}+\mathrm{2}}\:=\:\sum_{{n}=\mathrm{3}} ^{+\infty} \:\:\:\frac{{x}^{{n}−\mathrm{2}} }{{n}}\:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\sum_{{n}=\mathrm{3}} ^{+\infty} \:\frac{{x}^{{n}} }{{n}} \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:−{x}\:\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\:−\frac{{ln}\mid\mathrm{1}−{x}\mid}{{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${S}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}−{x}\mid\:−\frac{\mathrm{1}}{{x}}\left(−{ln}\mid\mathrm{1}−{x}\mid\:−{x}\right) \\ $$$$−\frac{{ln}\mid\mathrm{1}−{x}\mid}{\mathrm{2}{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}{x}}\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${S}\left({x}\right)=\left(−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right){ln}\mid\mathrm{1}−{x}\mid\:+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${S}\left({x}\right)=\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right){ln}\mid\mathrm{1}−{x}\mid\:−\frac{\mathrm{1}}{\mathrm{2}{x}}\:+\frac{\mathrm{3}}{\mathrm{4}}\:. \\ $$$$\left.\mathrm{2}\right)\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} {n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:=\:{S}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\left(−\frac{\mathrm{1}}{\mathrm{2}}\:−\mathrm{2}\:−\mathrm{2}\right){ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:\:+\mathrm{1}\:+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{4}\right){ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:+\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$=\:\frac{\mathrm{7}}{\mathrm{4}}\:−\frac{\mathrm{9}}{\mathrm{2}}\:\left({ln}\left(\mathrm{3}\right)\:−{ln}\left(\mathrm{2}\right)\right)\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *