Question Number 36689 by prof Abdo imad last updated on 04/Jun/18
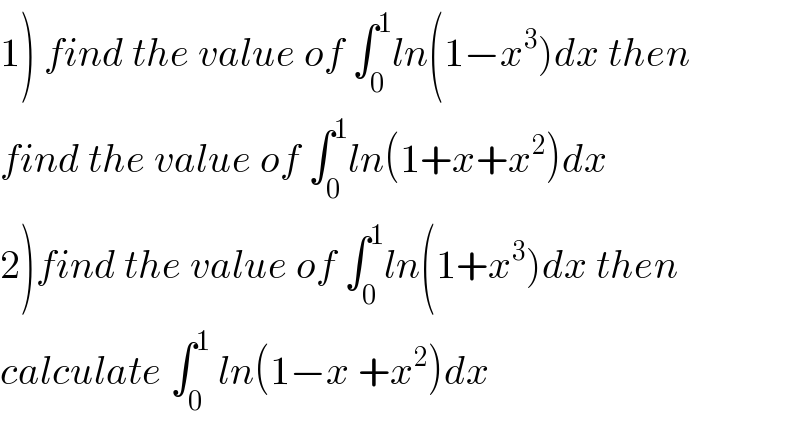
$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{3}} \right){dx}\:{then} \\ $$$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right){dx} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx}\:{then}\: \\ $$$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{x}\:+{x}^{\mathrm{2}} \right){dx} \\ $$
Commented by maxmathsup by imad last updated on 04/Aug/18
![1) let A = ∫_0 ^1 ln(1−x^3 )dx we have ln^′ (1−u)^ =−(1/(1−u)) =−Σ_(n=0) ^∞ u^n with ∣u∣<1 ⇒ ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (u^n /n) ⇒ A = −∫_0 ^1 (Σ_(n=1) ^∞ (x^(3n) /n) )dx =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^(3n) dx =−Σ_(n=1) ^∞ (1/(n(3n+1))) ⇒ −(A/3) =Σ_(n=1) ^∞ (1/(3n(3n+1))) =Σ_(n=1) ^∞ ((1/(3n))−(1/(3n+1))) let S_n =Σ_(k=1) ^n ((1/(3k)) −(1/(3k+1))) ⇒ S_n =(1/3)H_n −Σ_(k=1) ^n (1/(3k+1)) but Σ_(k=1) ^n (1/(3k+1))? we have Σ_(k=1) ^n (1/k) = Σ_(k=3p) (1/k) +Σ_(k=3p+1) (1/k) +Σ_(k=3p+2) (1/k) =Σ_(p=1) ^([(n/3)]) (1/(3p)) +Σ_(p=0) ^([((n−1)/3)]) (1/(3p+1)) + Σ_(p=0) ^([((n−2)/3)]) (1/(3p+2)) but Σ_(p=0) ^([((n−2)/3)]) (1/(3p+2)) =_(p=j−1) Σ_(j=1) ^([((n−2)/3)]−1) (1/(3j−1)) ⇒ Σ_(p=0) ^([((n−1)/3)]) (1/(3p+1)) +Σ_(p=1) ^([((n−5)/3)]) (1/(3p−1)) = H_n −(1/3) H_([(n/3)]) ...be continued...](https://www.tinkutara.com/question/Q41285.png)
$$\left.\mathrm{1}\right)\:{let}\:{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{3}} \right){dx}\:\:{we}\:{have}\:{ln}^{'} \left(\mathrm{1}−{u}\right)^{} \:=−\frac{\mathrm{1}}{\mathrm{1}−{u}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} {u}^{{n}} \\ $$$${with}\:\mid{u}\mid<\mathrm{1}\:\Rightarrow\:{ln}\left(\mathrm{1}−{u}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow \\ $$$${A}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{3}{n}} }{{n}}\:\right){dx}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{3}{n}} {dx}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\left(\mathrm{3}{n}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$−\frac{{A}}{\mathrm{3}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{3}{n}\left(\mathrm{3}{n}+\mathrm{1}\right)}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(\frac{\mathrm{1}}{\mathrm{3}{n}}−\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}}\right)\:{let}\: \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\left(\frac{\mathrm{1}}{\mathrm{3}{k}}\:−\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\right)\:\Rightarrow\:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}}{H}_{{n}} \:−\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\:\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}?\:\:\:\:\:{we}\:{have}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:=\:\sum_{{k}=\mathrm{3}{p}} \frac{\mathrm{1}}{{k}}\:+\sum_{{k}=\mathrm{3}{p}+\mathrm{1}} \frac{\mathrm{1}}{{k}}\:+\sum_{{k}=\mathrm{3}{p}+\mathrm{2}} \:\frac{\mathrm{1}}{{k}} \\ $$$$=\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{3}}\right]} \:\frac{\mathrm{1}}{\mathrm{3}{p}}\:\:+\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{3}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{3}{p}+\mathrm{1}}\:+\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{2}}{\mathrm{3}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{3}{p}+\mathrm{2}}\:\:{but} \\ $$$$\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{2}}{\mathrm{3}}\right]} \:\frac{\mathrm{1}}{\mathrm{3}{p}+\mathrm{2}}\:=_{{p}={j}−\mathrm{1}} \:\:\:\sum_{{j}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{2}}{\mathrm{3}}\right]−\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{3}{j}−\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{3}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{3}{p}+\mathrm{1}}\:+\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{5}}{\mathrm{3}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{3}{p}−\mathrm{1}}\:=\:{H}_{{n}} −\frac{\mathrm{1}}{\mathrm{3}}\:{H}_{\left[\frac{{n}}{\mathrm{3}}\right]} \:\:\:…{be}\:{continued}… \\ $$$$ \\ $$
