Menu Close

1-find-the-value-of-u-n-cos-nx-4-x-2-dx-2-find-the-nature-of-u-n-

Tinku Tara 0 Comments
Pin




Question Number 33129 by prof Abdo imad last updated on 10/Apr/18
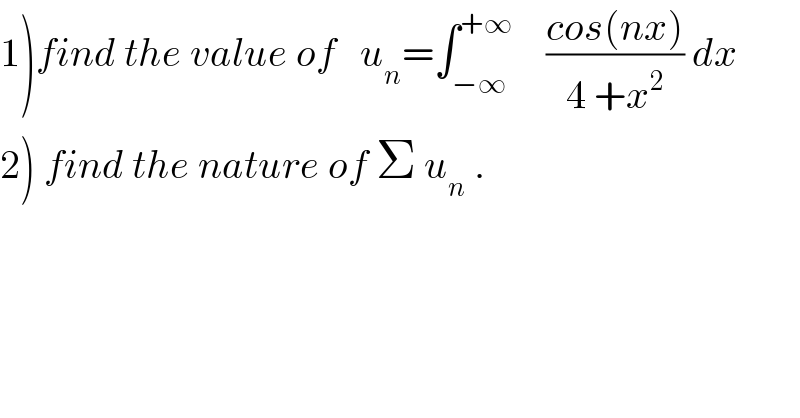
1)find the value of u_n =∫_(−∞) ^(+∞) ((cos(nx))/(4 +x^2 )) dx 2) find the nature of Σ u_n .
$$\left.\mathrm{1}\right){find}\:{the}\:{value}\:{of}\:\:\:{u}_{{n}} =\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{cos}\left({nx}\right)}{\mathrm{4}\:+{x}^{\mathrm{2}} }\:{dx} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{nature}\:{of}\:\Sigma\:{u}_{{n}} \:. \\ $$
Commented by prof Abdo imad last updated on 12/Apr/18
let calculate u_n by redidus theorem. u_n = Re( ∫_(−∞) ^(+∞) (e^(inx) /(4+x^2 ))dx) let consider ϕ(z) = (e^(inz) /(z^2 +4)) .poles of ϕ? ϕ(z) = (e^(inz) /((z −2i)(z+2i))) so the poles are 2i and −2i ∫_(−∞) ^(+∞) ϕ(z)dz = 2iπ Res(ϕ,2i) = (e^(in(2i)) /(4i)) = (e^(−2n) /(4i)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz = 2iπ (e^(−2n) /(4i)) = (π/2) e^(−2n) ⇒ u_n = (π/2) e^(−2n) 2) Σ_(n=0) ^(+∞) u_n =(π/2) Σ_(n=0) ^∞ (e^(−2) )^n =(π/2) (1/(1−e^(−2) )) = (π/(2( 1 −(1/e^2 )))) = ((π e^2 )/(2(e^2 −1))) .
$${let}\:{calculate}\:{u}_{{n}} \:{by}\:{redidus}\:{theorem}. \\ $$$${u}_{{n}} =\:{Re}\left(\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{e}^{{inx}} }{\mathrm{4}+{x}^{\mathrm{2}} }{dx}\right)\:{let}\:{consider} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{{inz}} }{{z}^{\mathrm{2}} \:+\mathrm{4}}\:.{poles}\:{of}\:\varphi? \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{{inz}} }{\left({z}\:−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)}\:\:{so}\:{the}\:{poles}\:{are} \\ $$$$\mathrm{2}{i}\:{and}\:−\mathrm{2}{i}\: \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\:\mathrm{2}{i}\pi\:{Res}\left(\varphi,\mathrm{2}{i}\right) \\ $$$$=\:\frac{{e}^{{in}\left(\mathrm{2}{i}\right)} }{\mathrm{4}{i}}\:=\:\frac{{e}^{−\mathrm{2}{n}} }{\mathrm{4}{i}}\:\Rightarrow\:\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\:\mathrm{2}{i}\pi\:\frac{{e}^{−\mathrm{2}{n}} }{\mathrm{4}{i}} \\ $$$$=\:\frac{\pi}{\mathrm{2}}\:{e}^{−\mathrm{2}{n}} \:\:\Rightarrow\:{u}_{{n}} \:=\:\frac{\pi}{\mathrm{2}}\:{e}^{−\mathrm{2}{n}} \\ $$$$\left.\mathrm{2}\right)\:\:\sum_{{n}=\mathrm{0}} ^{+\infty} \:{u}_{{n}} \:\:\:=\frac{\pi}{\mathrm{2}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left({e}^{−\mathrm{2}} \right)^{{n}} \:=\frac{\pi}{\mathrm{2}}\:\frac{\mathrm{1}}{\mathrm{1}−{e}^{−\mathrm{2}} } \\ $$$$=\:\frac{\pi}{\mathrm{2}\left(\:\mathrm{1}\:−\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\right)}\:=\:\frac{\pi\:{e}^{\mathrm{2}} }{\mathrm{2}\left({e}^{\mathrm{2}} \:−\mathrm{1}\right)}\:. \\ $$
Commented by prof Abdo imad last updated on 12/Apr/18
remark Im( ∫_(−∞) ^(+∞) (e^(inx) /(x^2 +4))dx)= ∫_(−∞) ^(+∞) ((sin(nx))/(x^2 +4))dx=0 brcausethe function is odd.
$${remark}\:\:{Im}\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{inx}} }{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}\right)=\:\int_{−\infty} ^{+\infty} \:\:\frac{{sin}\left({nx}\right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}=\mathrm{0} \\ $$$${brcausethe}\:{function}\:{is}\:{odd}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *