Question Number 146087 by mathmax by abdo last updated on 10/Jul/21
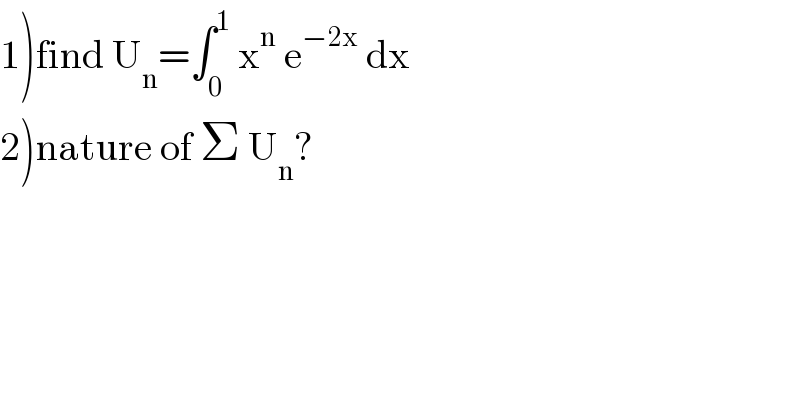
$$\left.\mathrm{1}\right)\mathrm{find}\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$\left.\mathrm{2}\right)\mathrm{nature}\:\mathrm{of}\:\Sigma\:\mathrm{U}_{\mathrm{n}} ? \\ $$
Answered by ArielVyny last updated on 24/Jul/21
![U_n =∫_0 ^1 x^n e^(−2x) dx x^n e^(−2x) =Σ_(n≥0) (((−1)^n 2^n x^(2n) )/(n!)) ∫_0 ^1 x^n e^(−2x) dx=Σ_(n≥0) (((−2)^n )/(n!))[(1/(2n+1))] U_n =Σ_(n≥0) (((−2)^n )/(n!(2n+1)))=Σ_(n≥0) (((−1)^n 2^n )/((2n+1)n!)) U_n CV](https://www.tinkutara.com/question/Q147880.png)
$${U}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {e}^{−\mathrm{2}{x}} {dx} \\ $$$${x}^{{n}} {e}^{−\mathrm{2}{x}} =\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{2}^{{n}} {x}^{\mathrm{2}{n}} }{{n}!} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {e}^{−\mathrm{2}{x}} {dx}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{2}\right)^{{n}} }{{n}!}\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right] \\ $$$${U}_{{n}} =\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{2}\right)^{{n}} }{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{2}^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!} \\ $$$${U}_{{n}} \:{CV} \\ $$$$ \\ $$
