Question Number 82872 by abdomathmax last updated on 25/Feb/20
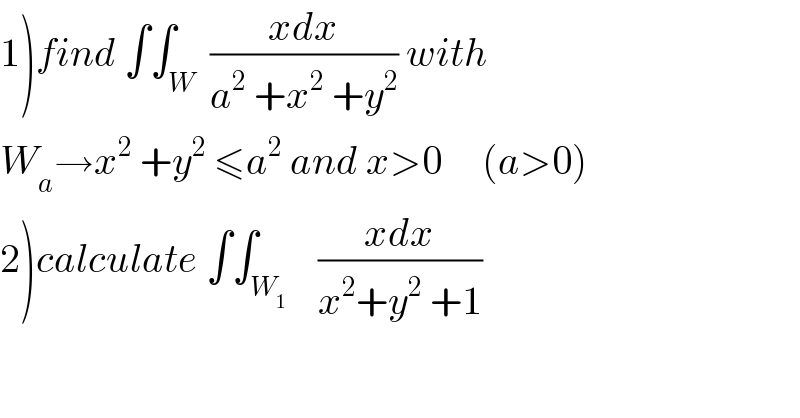
$$\left.\mathrm{1}\right){find}\:\int\int_{{W}} \:\frac{{xdx}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:{with} \\ $$$${W}_{{a}} \rightarrow{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant{a}^{\mathrm{2}} \:{and}\:{x}>\mathrm{0}\:\:\:\:\:\left({a}>\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right){calculate}\:\int\int_{{W}_{\mathrm{1}} } \:\:\:\frac{{xdx}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:+\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 25/Feb/20
![1) we use the diffeomorphism (r,θ)→(x,y)/x=rcosθ and y=rsinθ wehave x^2 +y^2 ≤a^2 ⇒0≤r≤a x>0 ⇒θ∈]−(π/2),(π/2)[ ⇒∫∫_W_a ((xdxdy)/(a^2 +r^2 )) =∫_0 ^a ∫_(−(π/2)) ^(π/2) ((rcosθ rdr dθ)/(a^2 +r^2 )) ∫_0 ^a (r^2 /(r^2 +a^2 )) dr ×∫_(−(π/2)) ^(π/2) cosθ dθ =2 ∫_0 ^a (r^2 /(r^2 +a^2 ))dr =2 ∫_0 ^a ((r^2 +a^2 −a^2 )/(r^2 +a^2 ))dr =2a −2a^2 ∫_0 ^a (dr/(r^2 +a^2 )) (ch. r=ax) =2a−2a^2 ∫_0 ^1 ((adx)/(a^2 (1+x^2 ))) =2a−2a [arctanx]_0 ^1 =2a−2a×(π/4) =(2−(π/2))a 2) ∫∫_W_1 ((xdx)/(x^2 +y^2 +1)) =_(a=1) 2−(π/2)](https://www.tinkutara.com/question/Q82916.png)
$$\left.\mathrm{1}\right)\:\:{we}\:{use}\:{the}\:{diffeomorphism}\:\:\left({r},\theta\right)\rightarrow\left({x},{y}\right)/{x}={rcos}\theta \\ $$$$\left.{and}\:{y}={rsin}\theta\:\:{wehave}\:\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant{r}\leqslant{a}\:\:\:{x}>\mathrm{0}\:\Rightarrow\theta\in\right]−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\left[\right. \\ $$$$\Rightarrow\int\int_{{W}_{{a}} } \:\frac{{xdxdy}}{{a}^{\mathrm{2}} \:+{r}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{{a}} \:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{rcos}\theta\:{rdr}\:{d}\theta}{{a}^{\mathrm{2}} \:+{r}^{\mathrm{2}} } \\ $$$$\:\int_{\mathrm{0}} ^{{a}} \:\frac{{r}^{\mathrm{2}} }{{r}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:{dr}\:×\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\theta\:{d}\theta\:\:=\mathrm{2}\:\int_{\mathrm{0}} ^{{a}} \:\frac{{r}^{\mathrm{2}} }{{r}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dr} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{{a}} \:\frac{{r}^{\mathrm{2}} \:+{a}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{r}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dr}\:=\mathrm{2}{a}\:−\mathrm{2}{a}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{{a}} \:\frac{{dr}}{{r}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:\:\left({ch}.\:{r}={ax}\right) \\ $$$$=\mathrm{2}{a}−\mathrm{2}{a}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{adx}}{{a}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=\mathrm{2}{a}−\mathrm{2}{a}\:\left[{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{2}{a}−\mathrm{2}{a}×\frac{\pi}{\mathrm{4}}\:=\left(\mathrm{2}−\frac{\pi}{\mathrm{2}}\right){a}\: \\ $$$$\left.\mathrm{2}\right)\:\int\int_{{W}_{\mathrm{1}} } \:\:\:\:\frac{{xdx}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+\mathrm{1}}\:=_{{a}=\mathrm{1}} \:\:\:\mathrm{2}−\frac{\pi}{\mathrm{2}} \\ $$
