Question Number 82442 by mathmax by abdo last updated on 21/Feb/20
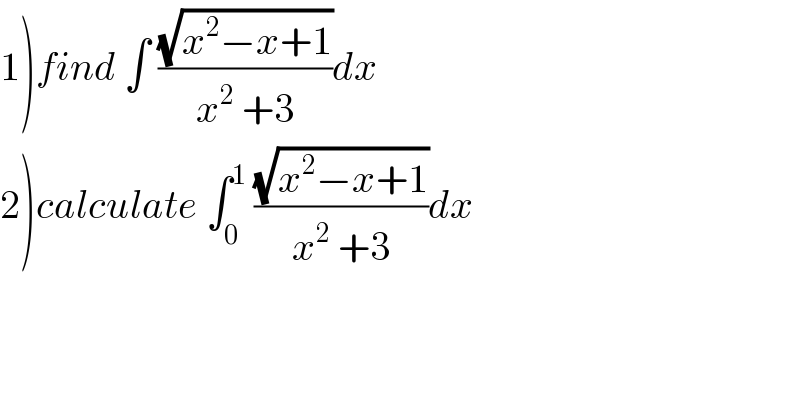
$$\left.\mathrm{1}\right){find}\:\int\:\frac{\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{{x}^{\mathrm{2}} \:+\mathrm{3}}{dx} \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{{x}^{\mathrm{2}} \:+\mathrm{3}}{dx} \\ $$
Commented by mathmax by abdo last updated on 23/Feb/20

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{x}^{\mathrm{2}} −{x}+\mathrm{1}\:=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\:\:{changement}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right) \\ $$$${give}\:{I}=\int\:\frac{\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{{x}^{\mathrm{2}} \:+\mathrm{3}}{dx}\:=\int\:\:\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\:}\:{ch}\left({t}\right)}{\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\right)^{\mathrm{2}} \:+\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\:\int\:\:\:\frac{{ch}^{\mathrm{2}} \left({t}\right)}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)+\mathrm{3}{sh}^{\mathrm{2}} \left({t}\right)\right)}{dt} \\ $$$$=\mathrm{3}\:\int\:\:\frac{{ch}^{\mathrm{2}} \left({t}\right)}{\mathrm{13}+\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)+\mathrm{3}{sh}^{\mathrm{2}} {t}}{dt}\:\:=\mathrm{3}\:\int\:\:\frac{\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}{\mathrm{13}+\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)+\mathrm{3}×\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}}{dt} \\ $$$$=\mathrm{3}\int\:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{26}+\mathrm{4}\sqrt{\mathrm{3}}{sh}\left({t}\right)+\mathrm{3}{ch}\left(\mathrm{2}{t}\right)−\mathrm{3}}{dt} \\ $$$$=\mathrm{3}\:\int\:\:\frac{\mathrm{1}+\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}{\mathrm{23}+\mathrm{4}\sqrt{\mathrm{3}}×\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}+\mathrm{3}×\frac{{e}^{\mathrm{2}{t}} +{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}{dt} \\ $$$$=\mathrm{3}\:\int\:\:\frac{\mathrm{2}+{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{46}+\mathrm{4}\sqrt{\mathrm{3}}\left({e}^{{t}} −{e}^{−{t}} \right)+\mathrm{3}{e}^{\mathrm{2}{t}} +\mathrm{3}{e}^{−\mathrm{2}{t}} }{dt} \\ $$$$=_{{e}^{{t}} \:={u}} \:\:\:\:\mathrm{3}\:\int\:\:\:\frac{\mathrm{2}+{u}^{\mathrm{2}} \:+{u}^{−\mathrm{2}} }{\mathrm{46}+\mathrm{4}\sqrt{\mathrm{3}}{u}\:−\mathrm{4}\sqrt{\mathrm{3}}{u}^{−\mathrm{1}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{3}{u}^{−\mathrm{2}} }\frac{{du}}{{u}} \\ $$$$=\mathrm{3}\:\int\:\:\:\frac{\mathrm{2}{u}^{\mathrm{2}} \:+{u}^{\mathrm{4}} \:+\mathrm{1}}{\mathrm{46}{u}^{\mathrm{3}} \:+\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{4}} −\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} \:+\mathrm{3}{u}^{\mathrm{5}} \:+\mathrm{3}{u}}{du} \\ $$$$=\mathrm{3}\:\int\:\:\frac{{u}^{\mathrm{4}} \:+\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}\left(\mathrm{3}{u}^{\mathrm{4}} \:+\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{3}} \:+\mathrm{46}{u}^{\mathrm{2}} +\mathrm{3}\right)}{du} \\ $$$${let}\:{decompose}\:{F}\left({u}\right)\:=\frac{{u}^{\mathrm{4}} \:+\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}\left(\mathrm{3}{u}^{\mathrm{4}} \:+\mathrm{4}\sqrt{\mathrm{3}}{u}^{\mathrm{3}} \:+\mathrm{46}\:{u}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$$…{be}\:{continued}… \\ $$
