Menu Close

1-findf-a-0-1-x-2-x-a-dx-with-a-gt-1-2-2-explicite-g-a-0-1-dx-x-2-x-a-3-calculate-0-1-dx-x-2-x-3-

Tinku Tara 0 Comments
Pin




Question Number 97800 by abdomathmax last updated on 09/Jun/20
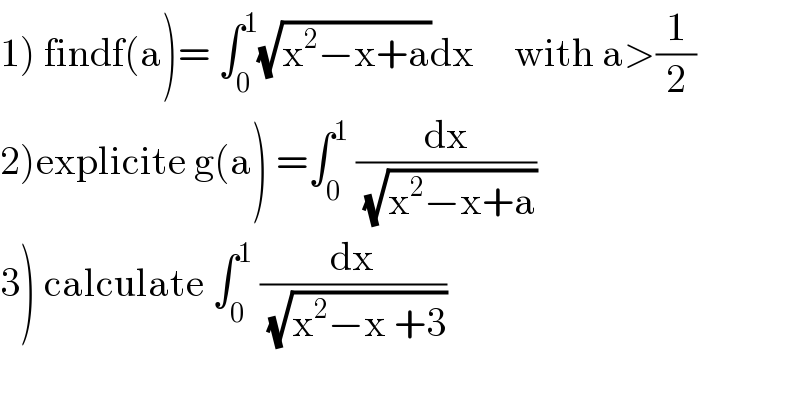
1) findf(a)= ∫_0 ^1 (√(x^2 −x+a))dx with a>(1/2) 2)explicite g(a) =∫_0 ^1 (dx/( (√(x^2 −x+a)))) 3) calculate ∫_0 ^1 (dx/( (√(x^2 −x +3))))
$$\left.\mathrm{1}\right)\:\mathrm{findf}\left(\mathrm{a}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{a}}\mathrm{dx}\:\:\:\:\:\mathrm{with}\:\mathrm{a}>\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\mathrm{explicite}\:\mathrm{g}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{a}}}\: \\ $$$$\left.\mathrm{3}\right)\:\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{3}}} \\ $$
Answered by niroj last updated on 09/Jun/20
(3).I= ∫_0 ^1 (dx/( (√(x^2 −x+3)))) = ∫_0 ^( 1) (1/( (√(x^2 −2.x.(1/2)+(1/4)−(1/4)+3))))dx = ∫_0 ^1 (1/( (√((x−(1/2))^2 −(((1−12)/4))))))dx = ∫_0 ^1 (1/( (√((x−(1/2))^2 +((( (√(11)))/2))^2 ))))dx Put ,x−(1/2)=t dx=dt if x=1, t=(1/2) if x= 0, t=−(1/2) = ∫_(−(1/2)) ^(1/2) (( 1)/( (√((t)^2 +(((√(11))/2))^2 ))))dt = [log (t+(√(t^2 +((11)/4))) )]^(1/2) _(−(1/2)) = {log ((1/2)+(√((1/4)+((11)/4))) )−log(−(1/2)+(√((1/4)+((11)/4))) )} = log(((1/2)+((2(√3))/2))/(−(1/2)+((2(√3))/2)))= log (( (√3)+ (1/2))/( (√3)− (1/2))) = log ((2(√3) +1)/( 2(√3) −1)) //.
$$\left(\mathrm{3}\right).\mathrm{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{3}}} \\ $$$$\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2}.\mathrm{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3}}}\mathrm{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}−\mathrm{12}}{\mathrm{4}}\right)}}\mathrm{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\:\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }}\mathrm{dx} \\ $$$$\:\mathrm{Put}\:,\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{t} \\ $$$$\:\:\:\:\mathrm{dx}=\mathrm{dt} \\ $$$$\:\:\mathrm{if}\:\mathrm{x}=\mathrm{1},\:\mathrm{t}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\mathrm{if}\:\mathrm{x}=\:\mathrm{0},\:\mathrm{t}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:=\:\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\:\mathrm{1}}{\:\sqrt{\left(\mathrm{t}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }}\mathrm{dt} \\ $$$$\:=\:\left[\mathrm{log}\:\left(\mathrm{t}+\sqrt{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}}}\:\:\:\right)\underset{−\frac{\mathrm{1}}{\mathrm{2}}} {\right]}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:\left\{\mathrm{log}\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{11}}{\mathrm{4}}}\:\:\:\right)−\mathrm{log}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{11}}{\mathrm{4}}}\:\:\right)\right\} \\ $$$$=\:\mathrm{log}\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}}{−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}}=\:\mathrm{log}\:\frac{\:\:\:\sqrt{\mathrm{3}}+\:\frac{\mathrm{1}}{\mathrm{2}}}{\:\:\:\sqrt{\mathrm{3}}−\:\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:\mathrm{log}\:\:\frac{\mathrm{2}\sqrt{\mathrm{3}}\:\:+\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{3}}\:−\mathrm{1}}\://. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 09/Jun/20
thank you sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by niroj last updated on 09/Jun/20
you welcome sir����������
Answered by 1549442205 last updated on 10/Jun/20
1)∫_0 ^1 (√(x^2 −x+a)) dx=∫_0 ^1 (√((x−(1/2))^2 +a−(1/4) )) dx=∫_0 ^1 (√(u^2 +m )) du(with u=x−(1/2),m=a−(1/4)) Putting (m/u^2 )+1=v^2 ⇒((−mdu)/u^3 )=vdv.We get F=∫((−vu^3 ×uv)/m)dv⇒(F/m)=−∫((v^2 mdv)/((v^2 −1)^2 ))=−(1/4)∫(((2v−1)/(v^2 −2v+1))+((2v+1)/(v^2 +2v+1)))dv =−(1/4)∫(((d(v^2 −2v+1))/(v^2 −2v+1))−∫((d(v^2 +2v+1))/(v^2 +2v+1))−(1/4)∫(dv/((v−1)^2 ))+(1/4)∫(dv/((v+1)^2 )) =((−1)/4)ln∣v^2 −2v+1∣−(1/4)ln∣v^2 +2v+1∣ +(1/(4(v−1)))−(1/(4(v+1)))=−(1/4)ln(v^2 −1)^2 +(1/(2(v^2 −1))) Hence,F=((−m)/2)ln(v^2 −1)+(m/(2(v^2 −1)))=(((1/4)−a)/2)ln∣(((1/4)−a)/((x−(1/2))^2 ))∣+((a−(1/4))/(2(x−(1/2))^2 )) ∫_0 ^1 (√(x^2 −x+a)) dx=F(1)−F(0)=0 since F(1)=F(0) 2/∫_0 ^1 (dx/( (√(x^2 −x+a)) ))=∫_0 ^1 ((d(x−(1/2)))/( (√((x−(1/2))^2 +((4a−1)/4)))))=ln∣x−(1/2)+(√(x^2 −x+a)) ∣_0 ^1 = =ln∣(1/2)+(√a) ∣−ln∣((−1)/2)+(√(a )) ∣=ln∣((1+2(√a))/(2(√a)−1))∣
$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{a}}\:\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{a}−\frac{\mathrm{1}}{\mathrm{4}}\:}\:\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{u}^{\mathrm{2}} +\mathrm{m}\:}\:\mathrm{du}\left(\mathrm{with}\:\mathrm{u}=\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}},\mathrm{m}=\mathrm{a}−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\mathrm{Putting}\:\frac{\mathrm{m}}{\mathrm{u}^{\mathrm{2}} }+\mathrm{1}=\mathrm{v}^{\mathrm{2}} \Rightarrow\frac{−\mathrm{mdu}}{\mathrm{u}^{\mathrm{3}} }=\mathrm{vdv}.\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{F}=\int\frac{−\mathrm{vu}^{\mathrm{3}} ×\mathrm{uv}}{\mathrm{m}}\mathrm{dv}\Rightarrow\frac{\mathrm{F}}{\mathrm{m}}=−\int\frac{\mathrm{v}^{\mathrm{2}} \mathrm{mdv}}{\left(\mathrm{v}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{\mathrm{2v}−\mathrm{1}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2v}+\mathrm{1}}+\frac{\mathrm{2v}+\mathrm{1}}{\mathrm{v}^{\mathrm{2}} +\mathrm{2v}+\mathrm{1}}\right)\mathrm{dv} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{\mathrm{d}\left(\mathrm{v}^{\mathrm{2}} −\mathrm{2v}+\mathrm{1}\right)}{\mathrm{v}^{\mathrm{2}} −\mathrm{2v}+\mathrm{1}}−\int\frac{\mathrm{d}\left(\mathrm{v}^{\mathrm{2}} +\mathrm{2v}+\mathrm{1}\right)}{\mathrm{v}^{\mathrm{2}} +\mathrm{2v}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{dv}}{\left(\mathrm{v}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{dv}}{\left(\mathrm{v}+\mathrm{1}\right)^{\mathrm{2}} }\right. \\ $$$$=\frac{−\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{v}^{\mathrm{2}} −\mathrm{2v}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{v}^{\mathrm{2}} +\mathrm{2v}+\mathrm{1}\mid \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{v}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{v}+\mathrm{1}\right)}=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{v}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{v}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\mathrm{Hence},\mathrm{F}=\frac{−\mathrm{m}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{v}^{\mathrm{2}} −\mathrm{1}\right)+\frac{\mathrm{m}}{\mathrm{2}\left(\mathrm{v}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{a}}{\mathrm{2}}\mathrm{ln}\mid\frac{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{a}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\mid+\frac{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{2}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{a}}\:\mathrm{dx}=\mathrm{F}\left(\mathrm{1}\right)−\mathrm{F}\left(\mathrm{0}\right)=\mathrm{0}\:\mathrm{since}\:\mathrm{F}\left(\mathrm{1}\right)=\mathrm{F}\left(\mathrm{0}\right) \\ $$$$\mathrm{2}/\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{a}}\:}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{d}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{4a}−\mathrm{1}}{\mathrm{4}}}}=\mathrm{ln}\mid\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{a}}\:\mid_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\mathrm{ln}\mid\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{a}}\:\mid−\mathrm{ln}\mid\frac{−\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{a}\:}\:\mid=\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{a}}}{\mathrm{2}\sqrt{\mathrm{a}}−\mathrm{1}}\mid \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 11/Jun/20
thanks sir.
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Answered by mathmax by abdo last updated on 11/Jun/20
1) we hsve x^2 −x+a =x^2 −2x×(1/2) +(1/4) +a−(1/4) =(x−(1/2))^2 +((4a−1)/4) so we do the changement x−(1/2) =((√(4a−1))/2)t ⇒ f(a) =∫_(−(1/( (√(4a−1))))) ^(1/( (√(4a−1)))) ((√(4a−1))/2)(√(1+t^2 ))((√(4a−1))/2)dt =((4a−1)/2) ∫_0 ^(1/( (√(4a−1)))) (√(1+t^2 ))dt =_(t =shu) ∫_0 ^(argsh((1/( (√(4a−1)))))) chu chu du =(1/2)∫_0 ^(argsh((1/( (√(4a−1)))))) (1+ch(2u))du =(1/2) argsh((1/( (√(4a−1))))) +(1/4) [sh(2u)]_0 ^(ln((1/( (√(4a−1))))+(√(1+(1/(4a−1)))))) =(1/2)ln((1/( (√(4a−1)))) +(√(1+(1/(4a−1))))) +(1/8)[ e^(2u) −e^(−2u) ]_0 ^(ln((1/( (√(4a−1))))+((2(√a))/( (√(4a−1)))))) =(1/2)ln((1/( (√(4a−1)))) +((2(√a))/( (√(4a−1))))) +(1/8){ (((1+2(√a))/( (√(4a−1)))))^2 −(((√(4a−1))/(1+2(√a))))^2 } f(a)=(1/2)ln(((1+2(√a))/( (√(4a−1))))) +(1/8){ (((1+2(√a))^2 )/(4a−1))−((4a−1)/((1+2(√a))^2 ))}
$$\left.\mathrm{1}\right)\:\mathrm{we}\:\mathrm{hsve}\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{a}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}×\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\mathrm{a}−\frac{\mathrm{1}}{\mathrm{4}}\:=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4a}−\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}} \frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\mathrm{dt}\:=\frac{\mathrm{4a}−\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}} \:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=_{\mathrm{t}\:=\mathrm{shu}} \:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)} \:\mathrm{chu}\:\mathrm{chu}\:\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)} \left(\mathrm{1}+\mathrm{ch}\left(\mathrm{2u}\right)\right)\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\:\left[\mathrm{sh}\left(\mathrm{2u}\right)\right]_{\mathrm{0}} ^{\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4a}−\mathrm{1}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4a}−\mathrm{1}}}\right)\:\:+\frac{\mathrm{1}}{\mathrm{8}}\left[\:\mathrm{e}^{\mathrm{2u}} −\mathrm{e}^{−\mathrm{2u}} \right]_{\mathrm{0}} ^{\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}+\frac{\mathrm{2}\sqrt{\mathrm{a}}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\:+\frac{\mathrm{2}\sqrt{\mathrm{a}}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{a}}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{a}}}\right)^{\mathrm{2}} \right\} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{a}}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\:\frac{\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{a}}\right)^{\mathrm{2}} }{\mathrm{4a}−\mathrm{1}}−\frac{\mathrm{4a}−\mathrm{1}}{\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{a}}\right)^{\mathrm{2}} }\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *