Question Number 57490 by Abdo msup. last updated on 05/Apr/19
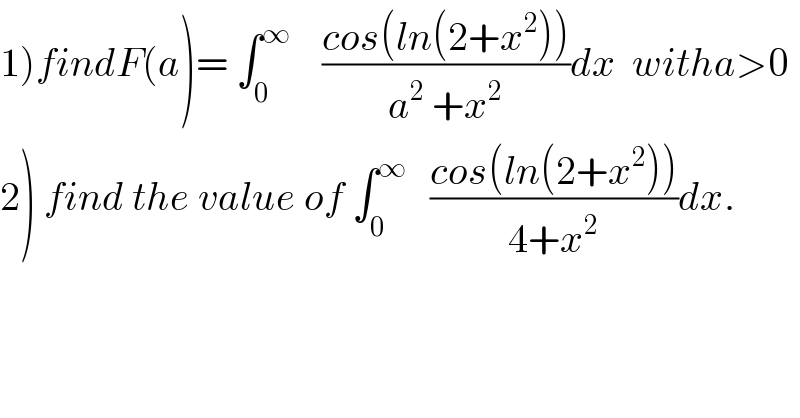
$$\left.\mathrm{1}\right){findF}\left({a}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{cos}\left({ln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)\right)}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }{dx}\:\:{witha}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left({ln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)\right)}{\mathrm{4}+{x}^{\mathrm{2}} }{dx}. \\ $$
Commented by maxmathsup by imad last updated on 06/Apr/19
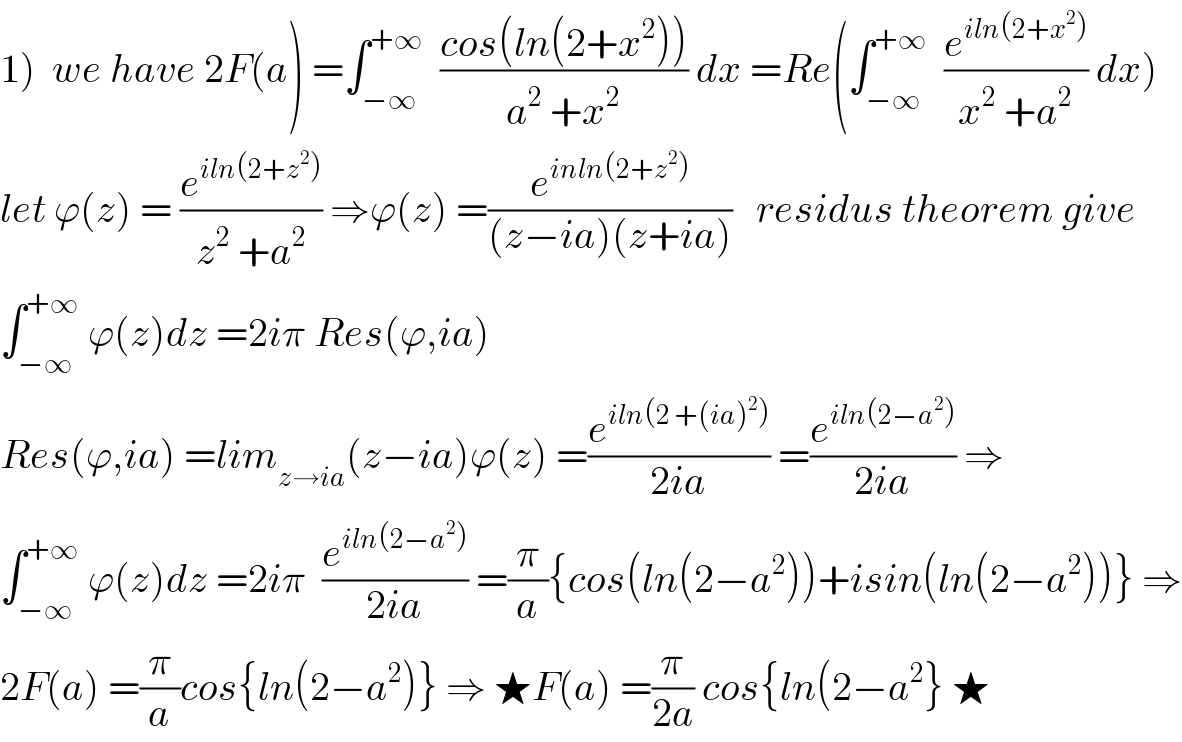
$$\left.\mathrm{1}\right)\:\:{we}\:{have}\:\mathrm{2}{F}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left({ln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)\right)}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:{dx}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{iln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)} }{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:{dx}\right) \\ $$$${let}\:\varphi\left({z}\right)\:=\:\frac{{e}^{{iln}\left(\mathrm{2}+{z}^{\mathrm{2}} \right)} }{{z}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:\Rightarrow\varphi\left({z}\right)\:=\frac{{e}^{{inln}\left(\mathrm{2}+{z}^{\mathrm{2}} \right)} }{\left({z}−{ia}\right)\left({z}+{ia}\right)}\:\:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{ia}\right) \\ $$$${Res}\left(\varphi,{ia}\right)\:={lim}_{{z}\rightarrow{ia}} \left({z}−{ia}\right)\varphi\left({z}\right)\:=\frac{{e}^{{iln}\left(\mathrm{2}\:+\left({ia}\right)^{\mathrm{2}} \right)} }{\mathrm{2}{ia}}\:=\frac{{e}^{{iln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)} }{\mathrm{2}{ia}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\:\frac{{e}^{{iln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)} }{\mathrm{2}{ia}}\:=\frac{\pi}{{a}}\left\{{cos}\left({ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)\right)+{isin}\left({ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)\right)\right\}\:\Rightarrow \\ $$$$\mathrm{2}{F}\left({a}\right)\:=\frac{\pi}{{a}}{cos}\left\{{ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)\right\}\:\Rightarrow\:\bigstar{F}\left({a}\right)\:=\frac{\pi}{\mathrm{2}{a}}\:{cos}\left\{{ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right\}\:\bigstar\right. \\ $$
Commented by maxmathsup by imad last updated on 06/Apr/19
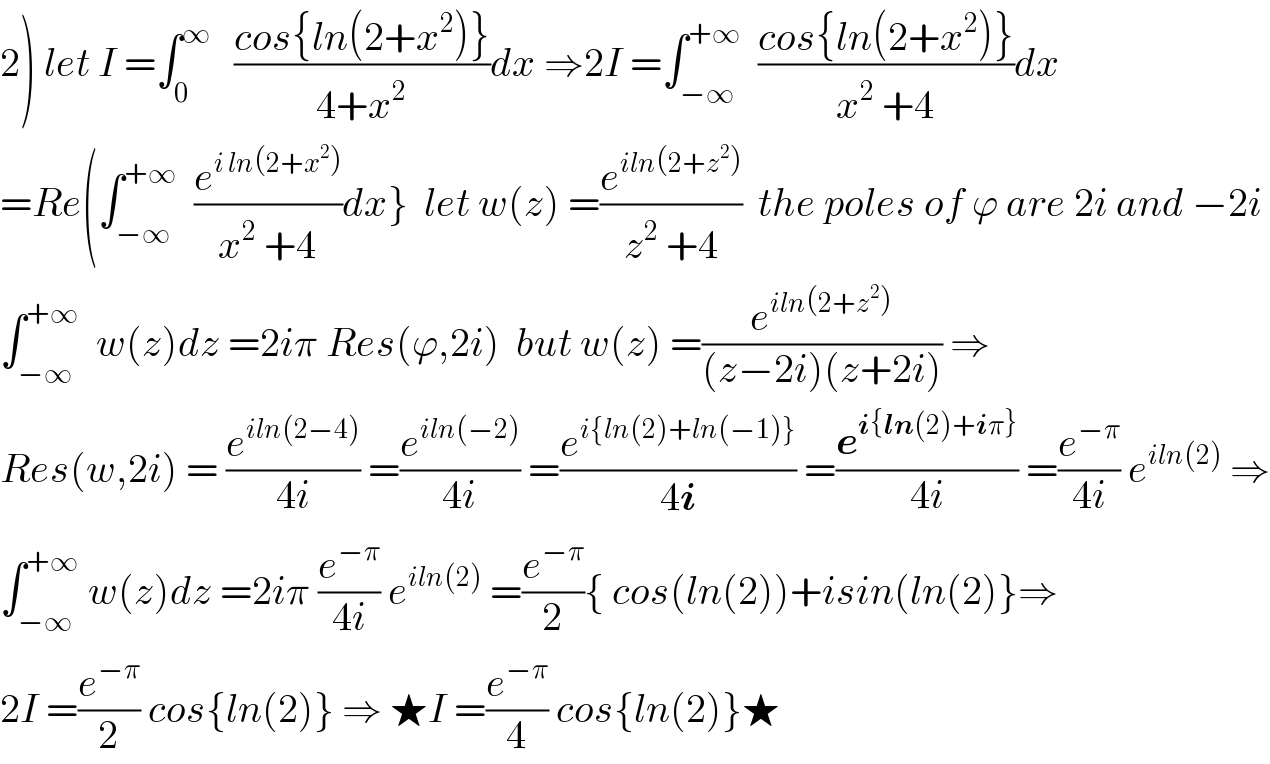
$$\left.\mathrm{2}\right)\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left\{{ln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)\right\}}{\mathrm{4}+{x}^{\mathrm{2}} }{dx}\:\Rightarrow\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left\{{ln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)\right\}}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx} \\ $$$$={Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{i}\:{ln}\left(\mathrm{2}+{x}^{\mathrm{2}} \right)} }{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}\right\}\:\:{let}\:{w}\left({z}\right)\:=\frac{{e}^{{iln}\left(\mathrm{2}+{z}^{\mathrm{2}} \right)} }{{z}^{\mathrm{2}} \:+\mathrm{4}}\:\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\mathrm{2}{i}\:{and}\:−\mathrm{2}{i} \\ $$$$\int_{−\infty} ^{+\infty} \:\:{w}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,\mathrm{2}{i}\right)\:\:{but}\:{w}\left({z}\right)\:=\frac{{e}^{{iln}\left(\mathrm{2}+{z}^{\mathrm{2}} \right)} }{\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)}\:\Rightarrow \\ $$$${Res}\left({w},\mathrm{2}{i}\right)\:=\:\frac{{e}^{{iln}\left(\mathrm{2}−\mathrm{4}\right)} }{\mathrm{4}{i}}\:=\frac{{e}^{{iln}\left(−\mathrm{2}\right)} }{\mathrm{4}{i}}\:=\frac{{e}^{{i}\left\{{ln}\left(\mathrm{2}\right)+{ln}\left(−\mathrm{1}\right)\right\}} }{\mathrm{4}\boldsymbol{{i}}}\:=\frac{\boldsymbol{{e}}^{\boldsymbol{{i}}\left\{\boldsymbol{{ln}}\left(\mathrm{2}\right)+\boldsymbol{{i}}\pi\right\}} }{\mathrm{4}{i}}\:=\frac{{e}^{−\pi} }{\mathrm{4}{i}}\:{e}^{{iln}\left(\mathrm{2}\right)} \:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{w}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{{e}^{−\pi} }{\mathrm{4}{i}}\:{e}^{{iln}\left(\mathrm{2}\right)} \:=\frac{{e}^{−\pi} }{\mathrm{2}}\left\{\:{cos}\left({ln}\left(\mathrm{2}\right)\right)+{isin}\left({ln}\left(\mathrm{2}\right)\right\}\Rightarrow\right. \\ $$$$\mathrm{2}{I}\:=\frac{{e}^{−\pi} }{\mathrm{2}}\:{cos}\left\{{ln}\left(\mathrm{2}\right)\right\}\:\Rightarrow\:\bigstar{I}\:=\frac{{e}^{−\pi} }{\mathrm{4}}\:{cos}\left\{{ln}\left(\mathrm{2}\right)\right\}\bigstar \\ $$
Answered by einsteindrmaths@hotmail.fr last updated on 05/Apr/19
![a)f(a)=(1/2)∫_(−∞) ^∞ ((cosln (2+x^2 ))/(a^2 +x^2 ))dx letf(z)=((cos(ln(2+z^2 )))/(a^2 +z^2 )) withe z≠{−i(√2) .i(√2) } res(f(z).ia)=lim_(z→ia) ((cos(ln(z^2 +2)))/((z+ia)))=((cos(ln(2−a^2 )))/(2ia)) we get f(a)=(1/2)2iπ×((cos(ln(2−a^2 )))/(2ia))=((πcos(ln(2−a^2 )))/(2a)) for a≠i(√2) 2)f(2)=π((cos(ln(−2)))/4)=(π/4)[cos( ln2).cosh(π)+sin (ln2) sh(π) ]](https://www.tinkutara.com/question/Q57497.png)
$$ \\ $$$$ \\ $$$$\left.{a}\right){f}\left({a}\right)=\frac{\mathrm{1}}{\mathrm{2}}\underset{−\infty} {\overset{\infty} {\int}}\frac{{cos}\mathrm{ln}\:\left(\mathrm{2}+{x}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx} \\ $$$${letf}\left({z}\right)=\frac{{cos}\left({ln}\left(\mathrm{2}+{z}^{\mathrm{2}} \right)\right)}{{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }\:\:{withe}\:{z}\neq\left\{−{i}\sqrt{\mathrm{2}}\:.{i}\sqrt{\mathrm{2}}\:\right\} \\ $$$${res}\left({f}\left({z}\right).{ia}\right)={lim}_{{z}\rightarrow{ia}} \frac{{cos}\left({ln}\left({z}^{\mathrm{2}} +\mathrm{2}\right)\right)}{\left({z}+{ia}\right)}=\frac{{cos}\left({ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)\right)}{\mathrm{2}{ia}} \\ $$$${we}\:{get}\:{f}\left({a}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}{i}\pi×\frac{{cos}\left({ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)\right)}{\mathrm{2}{ia}}=\frac{\pi{cos}\left({ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)\right)}{\mathrm{2}{a}}\:{for}\:{a}\neq{i}\sqrt{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right){f}\left(\mathrm{2}\right)=\pi\frac{{cos}\left({ln}\left(−\mathrm{2}\right)\right)}{\mathrm{4}}=\frac{\pi}{\mathrm{4}}\left[\mathrm{cos}\left(\:{ln}\mathrm{2}\right).\mathrm{cosh}\left(\pi\right)+{sin}\:\left({ln}\mathrm{2}\right)\:{sh}\left(\pi\right)\:\right] \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 05/Apr/19
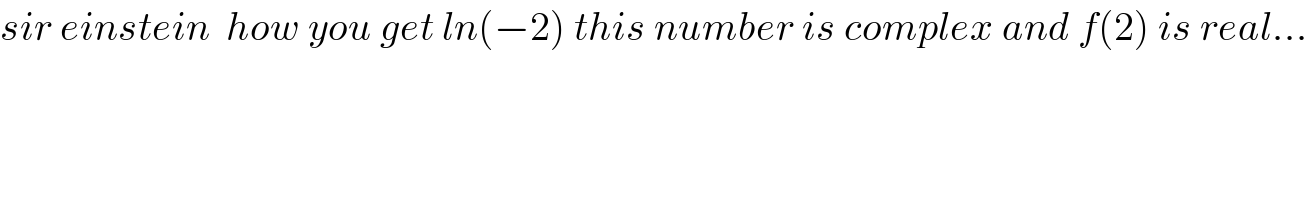
$${sir}\:{einstein}\:\:{how}\:{you}\:{get}\:{ln}\left(−\mathrm{2}\right)\:{this}\:{number}\:{is}\:{complex}\:{and}\:{f}\left(\mathrm{2}\right)\:{is}\:{real}… \\ $$
Commented by einsteindrmaths@hotmail.fr last updated on 06/Apr/19
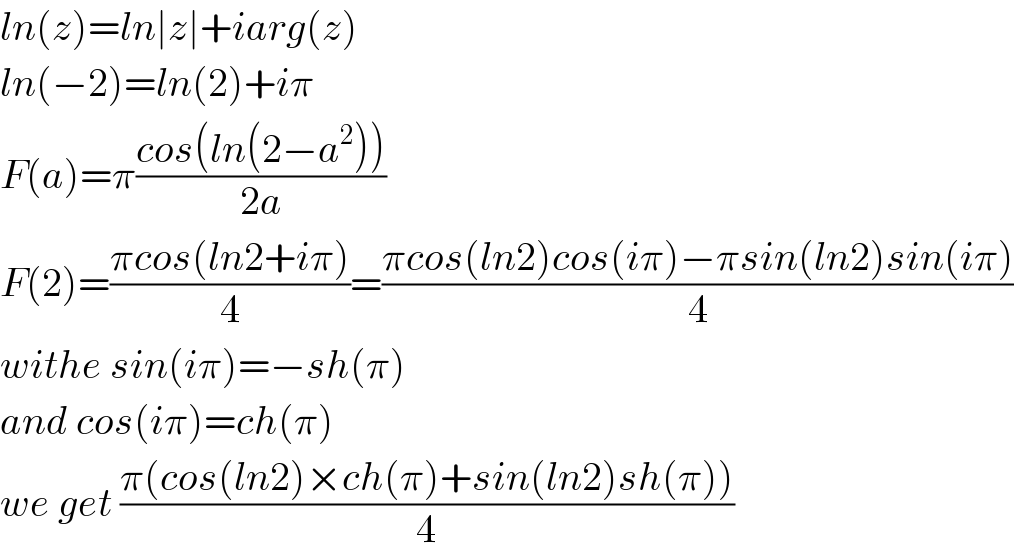
$${ln}\left({z}\right)={ln}\mid{z}\mid+{iarg}\left({z}\right) \\ $$$${ln}\left(−\mathrm{2}\right)={ln}\left(\mathrm{2}\right)+{i}\pi \\ $$$${F}\left({a}\right)=\pi\frac{{cos}\left({ln}\left(\mathrm{2}−{a}^{\mathrm{2}} \right)\right)}{\mathrm{2}{a}} \\ $$$${F}\left(\mathrm{2}\right)=\frac{\pi{cos}\left({ln}\mathrm{2}+{i}\pi\right)}{\mathrm{4}}=\frac{\pi{cos}\left({ln}\mathrm{2}\right){cos}\left({i}\pi\right)−\pi{sin}\left({ln}\mathrm{2}\right){sin}\left({i}\pi\right)}{\mathrm{4}} \\ $$$${withe}\:{sin}\left({i}\pi\right)=−{sh}\left(\pi\right) \\ $$$${and}\:{cos}\left({i}\pi\right)={ch}\left(\pi\right) \\ $$$${we}\:{get}\:\frac{\pi\left({cos}\left({ln}\mathrm{2}\right)×{ch}\left(\pi\right)+{sin}\left({ln}\mathrm{2}\right){sh}\left(\pi\right)\right)}{\mathrm{4}} \\ $$
