Question Number 128232 by math35 last updated on 05/Jan/21
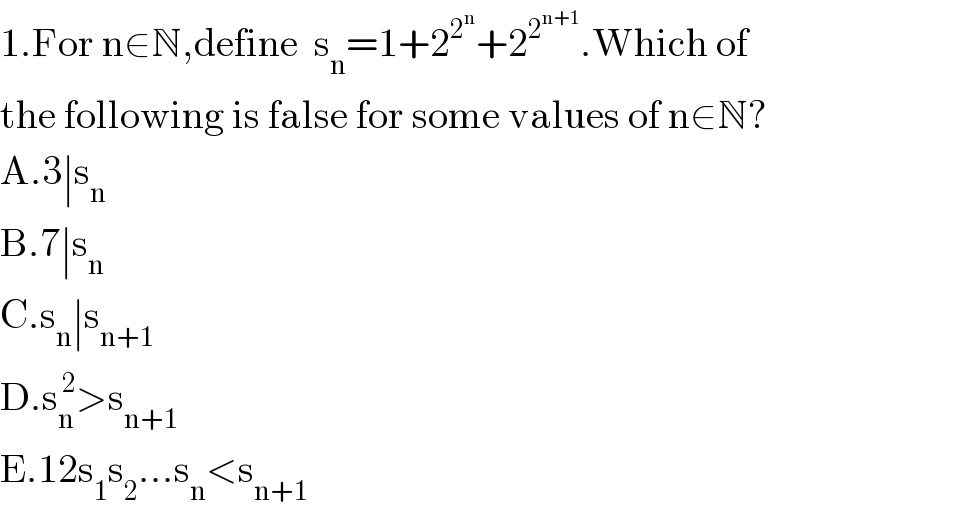
$$\mathrm{1}.\mathrm{For}\:\mathrm{n}\in\mathbb{N},\mathrm{define}\:\:\mathrm{s}_{\mathrm{n}} =\mathrm{1}+\mathrm{2}^{\mathrm{2}^{\mathrm{n}} } +\mathrm{2}^{\mathrm{2}^{\mathrm{n}+\mathrm{1}} } .\mathrm{Which}\:\mathrm{of}\: \\ $$$$\mathrm{the}\:\mathrm{following}\:\mathrm{is}\:\mathrm{false}\:\mathrm{for}\:\mathrm{some}\:\mathrm{values}\:\mathrm{of}\:\mathrm{n}\in\mathbb{N}? \\ $$$$\mathrm{A}.\mathrm{3}\mid\mathrm{s}_{\mathrm{n}} \\ $$$$\mathrm{B}.\mathrm{7}\mid\mathrm{s}_{\mathrm{n}} \\ $$$$\mathrm{C}.\mathrm{s}_{\mathrm{n}} \mid\mathrm{s}_{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{D}.\mathrm{s}_{\mathrm{n}} ^{\:\mathrm{2}} >\mathrm{s}_{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{E}.\mathrm{12s}_{\mathrm{1}} \mathrm{s}_{\mathrm{2}} …\mathrm{s}_{\mathrm{n}} <\mathrm{s}_{\mathrm{n}+\mathrm{1}} \\ $$
