Menu Close

1-give-D-n-1-o-for-f-x-1-x-2-2-drcompose-inside-R-x-the-fraction-F-x-1-x-n-x-2-

Tinku Tara 0 Comments
Pin




Question Number 33335 by prof Abdo imad last updated on 14/Apr/18
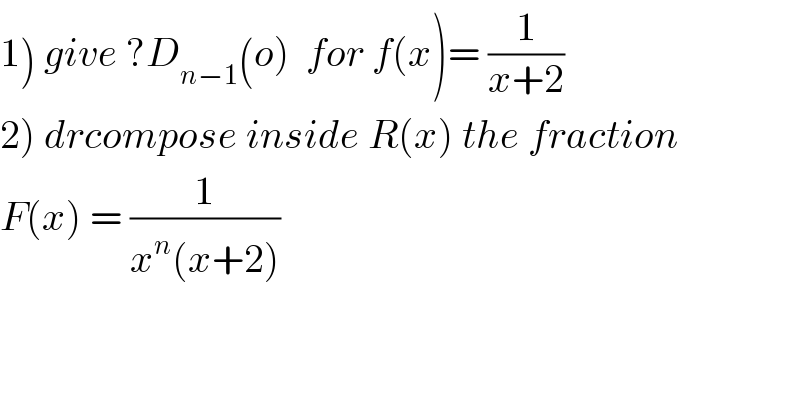
1) give ?D_(n−1) (o) for f(x)= (1/(x+2)) 2) drcompose inside R(x) the fraction F(x) = (1/(x^n (x+2)))
$$\left.\mathrm{1}\right)\:{give}\:?{D}_{{n}−\mathrm{1}} \left({o}\right)\:\:{for}\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{{x}+\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:{drcompose}\:{inside}\:{R}\left({x}\right)\:{the}\:{fraction} \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}^{{n}} \left({x}+\mathrm{2}\right)} \\ $$
Commented by prof Abdo imad last updated on 25/Apr/18
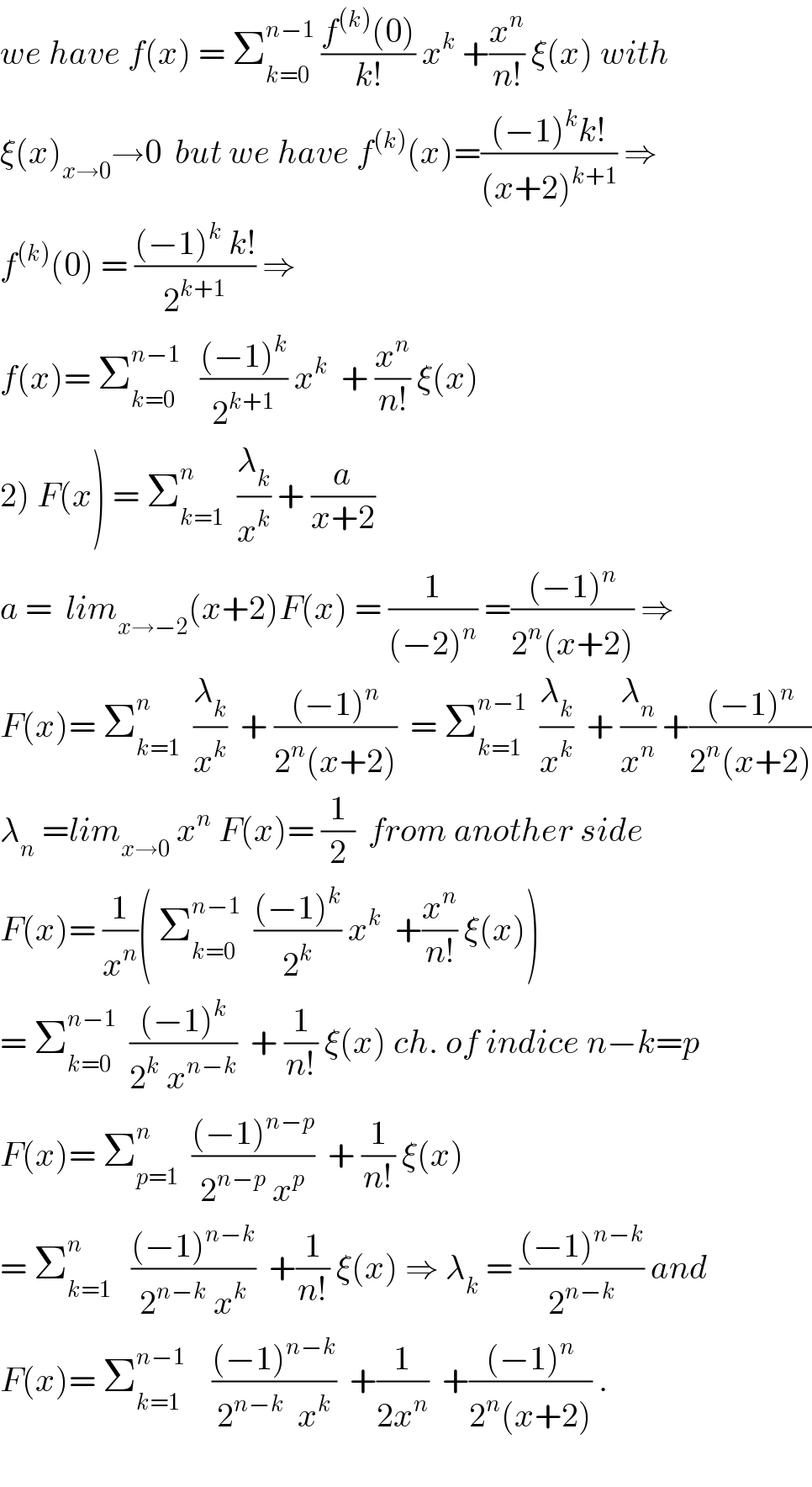
we have f(x) = Σ_(k=0) ^(n−1) ((f^((k)) (0))/(k!)) x^k +(x^n /(n!)) ξ(x) with ξ(x)_(x→0) →0 but we have f^((k)) (x)=(((−1)^k k!)/((x+2)^(k+1) )) ⇒ f^((k)) (0) = (((−1)^k k!)/2^(k+1) ) ⇒ f(x)= Σ_(k=0) ^(n−1) (((−1)^k )/2^(k+1) ) x^k + (x^n /(n!)) ξ(x) 2) F(x) = Σ_(k=1) ^n (λ_k /x^k ) + (a/(x+2)) a = lim_(x→−2) (x+2)F(x) = (1/((−2)^n )) =(((−1)^n )/(2^n (x+2))) ⇒ F(x)= Σ_(k=1) ^n (λ_k /x^k ) + (((−1)^n )/(2^n (x+2))) = Σ_(k=1) ^(n−1) (λ_k /x^k ) + (λ_n /x^n ) +(((−1)^n )/(2^n (x+2))) λ_n =lim_(x→0) x^n F(x)= (1/2) from another side F(x)= (1/x^n )( Σ_(k=0) ^(n−1) (((−1)^k )/2^k ) x^k +(x^n /(n!)) ξ(x)) = Σ_(k=0) ^(n−1) (((−1)^k )/(2^k x^(n−k) )) + (1/(n!)) ξ(x) ch. of indice n−k=p F(x)= Σ_(p=1) ^n (((−1)^(n−p) )/(2^(n−p) x^p )) + (1/(n!)) ξ(x) = Σ_(k=1) ^n (((−1)^(n−k) )/(2^(n−k) x^k )) +(1/(n!)) ξ(x) ⇒ λ_k = (((−1)^(n−k) )/2^(n−k) ) and F(x)= Σ_(k=1) ^(n−1) (((−1)^(n−k) )/(2^(n−k) x^k )) +(1/(2x^n )) +(((−1)^n )/(2^n (x+2))) .
$${we}\:{have}\:{f}\left({x}\right)\:=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{f}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:{x}^{{k}} \:+\frac{{x}^{{n}} }{{n}!}\:\xi\left({x}\right)\:{with} \\ $$$$\xi\left({x}\right)_{{x}\rightarrow\mathrm{0}} \rightarrow\mathrm{0}\:\:{but}\:{we}\:{have}\:{f}^{\left({k}\right)} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{k}} {k}!}{\left({x}+\mathrm{2}\right)^{{k}+\mathrm{1}} }\:\Rightarrow \\ $$$${f}^{\left({k}\right)} \left(\mathrm{0}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{k}!}{\mathrm{2}^{{k}+\mathrm{1}} }\:\Rightarrow \\ $$$${f}\left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}+\mathrm{1}} }\:{x}^{{k}} \:\:+\:\frac{{x}^{{n}} }{{n}!}\:\xi\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{F}\left({x}\right)\:=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\lambda_{{k}} }{{x}^{{k}} }\:+\:\frac{{a}}{{x}+\mathrm{2}} \\ $$$${a}\:=\:\:{lim}_{{x}\rightarrow−\mathrm{2}} \left({x}+\mathrm{2}\right){F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\left(−\mathrm{2}\right)^{{n}} }\:=\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left({x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\lambda_{{k}} }{{x}^{{k}} }\:\:+\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left({x}+\mathrm{2}\right)}\:\:=\:\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\:\frac{\lambda_{{k}} }{{x}^{{k}} }\:\:+\:\frac{\lambda_{{n}} }{{x}^{{n}} }\:+\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left({x}+\mathrm{2}\right)} \\ $$$$\lambda_{{n}} \:={lim}_{{x}\rightarrow\mathrm{0}} \:{x}^{{n}} \:{F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:{from}\:{another}\:{side} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{{x}^{{n}} }\left(\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\:{x}^{{k}} \:\:+\frac{{x}^{{n}} }{{n}!}\:\xi\left({x}\right)\right) \\ $$$$=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} \:{x}^{{n}−{k}} }\:\:+\:\frac{\mathrm{1}}{{n}!}\:\xi\left({x}\right)\:{ch}.\:{of}\:{indice}\:{n}−{k}={p} \\ $$$${F}\left({x}\right)=\:\sum_{{p}=\mathrm{1}} ^{{n}} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−{p}} }{\mathrm{2}^{{n}−{p}} \:{x}^{{p}} }\:\:+\:\frac{\mathrm{1}}{{n}!}\:\xi\left({x}\right) \\ $$$$=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−{k}} }{\mathrm{2}^{{n}−{k}} \:{x}^{{k}} }\:\:+\frac{\mathrm{1}}{{n}!}\:\xi\left({x}\right)\:\Rightarrow\:\lambda_{{k}} \:=\:\frac{\left(−\mathrm{1}\right)^{{n}−{k}} }{\mathrm{2}^{{n}−{k}} }\:{and} \\ $$$${F}\left({x}\right)=\:\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−{k}} }{\mathrm{2}^{{n}−{k}} \:\:{x}^{{k}} }\:\:+\frac{\mathrm{1}}{\mathrm{2}{x}^{{n}} }\:\:+\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} \left({x}+\mathrm{2}\right)}\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *