Question Number 122903 by Khalmohmmad last updated on 20/Nov/20

$$\left(\frac{\mathrm{1}+{i}}{\mathrm{1}−{i}}\right)^{\mathrm{50}} =? \\ $$
Answered by Dwaipayan Shikari last updated on 20/Nov/20
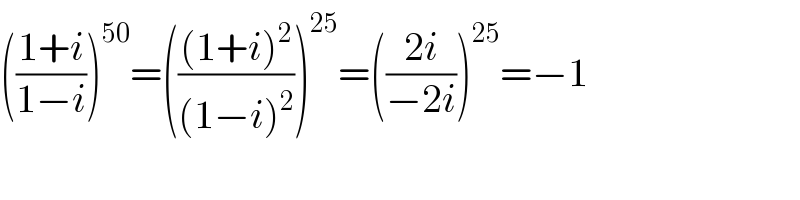
$$\left(\frac{\mathrm{1}+{i}}{\mathrm{1}−{i}}\right)^{\mathrm{50}} =\left(\frac{\left(\mathrm{1}+{i}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{i}\right)^{\mathrm{2}} }\right)^{\mathrm{25}} =\left(\frac{\mathrm{2}{i}}{−\mathrm{2}{i}}\right)^{\mathrm{25}} =−\mathrm{1} \\ $$
Answered by Bird last updated on 20/Nov/20
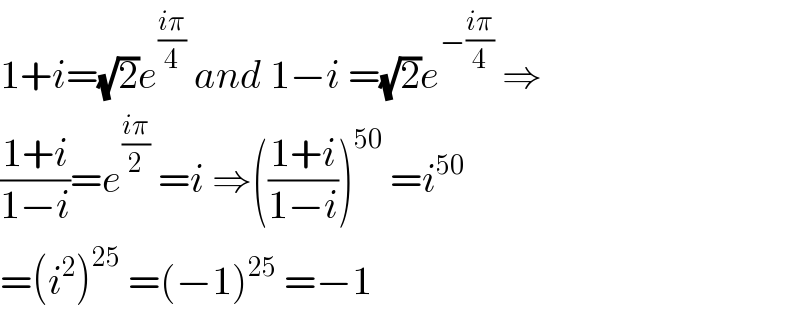
$$\mathrm{1}+{i}=\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{and}\:\mathrm{1}−{i}\:=\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}+{i}}{\mathrm{1}−{i}}={e}^{\frac{{i}\pi}{\mathrm{2}}} \:={i}\:\Rightarrow\left(\frac{\mathrm{1}+{i}}{\mathrm{1}−{i}}\right)^{\mathrm{50}} \:={i}^{\mathrm{50}} \\ $$$$=\left({i}^{\mathrm{2}} \right)^{\mathrm{25}} \:=\left(−\mathrm{1}\right)^{\mathrm{25}} \:=−\mathrm{1} \\ $$
