Question Number 81966 by naka3546 last updated on 17/Feb/20
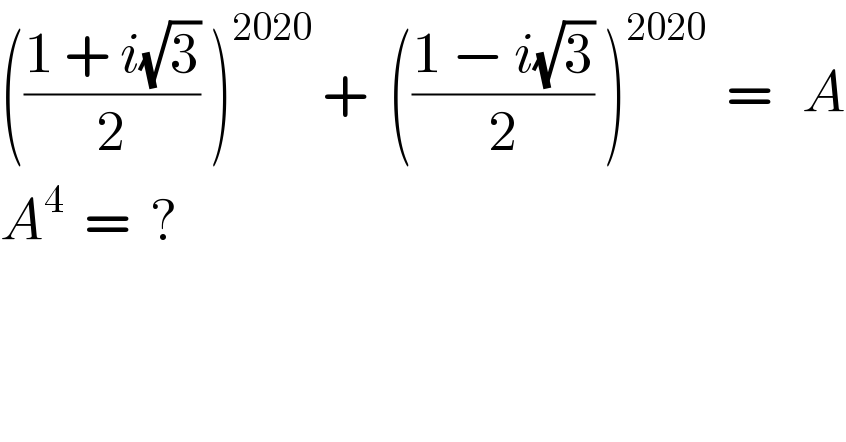
$$\left(\frac{\mathrm{1}\:+\:{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\right)^{\mathrm{2020}} \:+\:\:\left(\frac{\mathrm{1}\:−\:{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\right)^{\mathrm{2020}} \:\:=\:\:\:{A} \\ $$$${A}^{\mathrm{4}} \:\:=\:\:? \\ $$
Answered by TANMAY PANACEA last updated on 17/Feb/20
![(1/2)=cos(π/3) ((√3)/2)=sin(π/3) (cos(π/3)+isin(π/3))^(2020) +(cos(π/3)−isin(π/3))^(2020) (e^(i×(π/3)) )^(2020) +(e^(−i×(π/3)) )^(2020) e^(iθ) +e^(−iθ) =2cosθ where[θ=((2020π)/3)] A=2cosθ A^4 =16(cosθ)^4 now cos(((2020π)/3)) cos(2020×60) =cos(121200) =cos(336×360+240) =−cos60 =((−1)/2) so required answer is16× (((−1)/2))^4 =1](https://www.tinkutara.com/question/Q81967.png)
$$\frac{\mathrm{1}}{\mathrm{2}}={cos}\frac{\pi}{\mathrm{3}}\:\:\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={sin}\frac{\pi}{\mathrm{3}} \\ $$$$\left({cos}\frac{\pi}{\mathrm{3}}+{isin}\frac{\pi}{\mathrm{3}}\right)^{\mathrm{2020}} +\left({cos}\frac{\pi}{\mathrm{3}}−{isin}\frac{\pi}{\mathrm{3}}\right)^{\mathrm{2020}} \\ $$$$\left({e}^{{i}×\frac{\pi}{\mathrm{3}}} \right)^{\mathrm{2020}} +\left({e}^{−{i}×\frac{\pi}{\mathrm{3}}} \right)^{\mathrm{2020}} \\ $$$${e}^{{i}\theta} +{e}^{−{i}\theta} =\mathrm{2}{cos}\theta\:\:\:{where}\left[\theta=\frac{\mathrm{2020}\pi}{\mathrm{3}}\right] \\ $$$${A}=\mathrm{2}{cos}\theta \\ $$$${A}^{\mathrm{4}} =\mathrm{16}\left({cos}\theta\right)^{\mathrm{4}} \\ $$$${now}\:{cos}\left(\frac{\mathrm{2020}\pi}{\mathrm{3}}\right) \\ $$$${cos}\left(\mathrm{2020}×\mathrm{60}\right) \\ $$$$={cos}\left(\mathrm{121200}\right) \\ $$$$={cos}\left(\mathrm{336}×\mathrm{360}+\mathrm{240}\right) \\ $$$$=−{cos}\mathrm{60} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{required}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}}\mathrm{16}×\:\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} =\mathrm{1} \\ $$
Commented by naka3546 last updated on 17/Feb/20
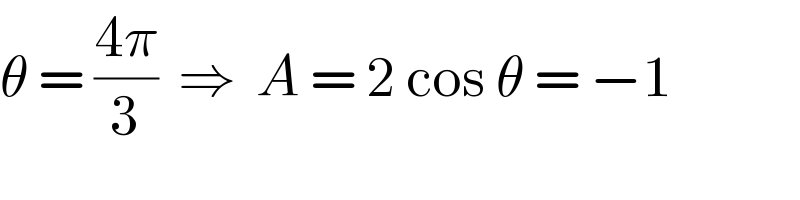
$$\theta\:=\:\frac{\mathrm{4}\pi}{\mathrm{3}}\:\:\Rightarrow\:\:{A}\:=\:\mathrm{2}\:\mathrm{cos}\:\theta\:=\:−\mathrm{1} \\ $$
