Question Number 48227 by gunawan last updated on 21/Nov/18

$$\left(\mathrm{1}−{i}\right)^{\mathrm{4}{i}} =.. \\ $$
Answered by Smail last updated on 21/Nov/18
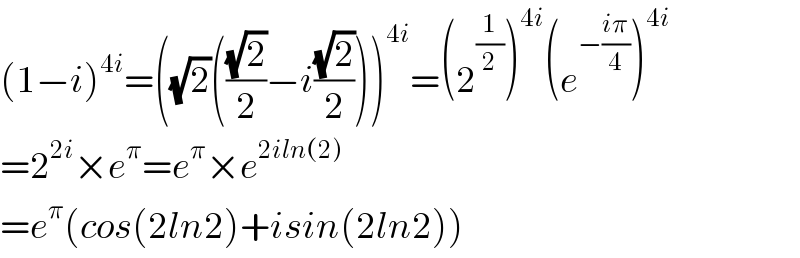
$$\left(\mathrm{1}−{i}\right)^{\mathrm{4}{i}} =\left(\sqrt{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\right)^{\mathrm{4}{i}} =\left(\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\mathrm{4}{i}} \left({e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{\mathrm{4}{i}} \\ $$$$=\mathrm{2}^{\mathrm{2}{i}} ×{e}^{\pi} ={e}^{\pi} ×{e}^{\mathrm{2}{iln}\left(\mathrm{2}\right)} \\ $$$$={e}^{\pi} \left({cos}\left(\mathrm{2}{ln}\mathrm{2}\right)+{isin}\left(\mathrm{2}{ln}\mathrm{2}\right)\right) \\ $$
