Menu Close

1-i-Evaluate-1-sin-x-cos-x-2-dx-ii-Evaluate-2-2-2-x-2-2-x-2-x-dx-iii-Evaluate-cos-3-x-sin-2-x-sin-x-dx-2-cosec-tan-1-cos-cot-1-sec-sin-1-a-What-3-Prove-that-s

Tinku Tara 0 Comments
Pin




Question Number 65011 by AnjanDey last updated on 24/Jul/19
1.(i)Evaluate:∫(1/(sin x−cos x+(√2)))dx (ii)Evaluate:∫2^2^2^x 2^2^x 2^x dx (iii)Evaluate:∫((cos^3 x)/(sin^2 x+sin x))dx 2.cosec [tan^(−1) {cos (cot^(−1) (sec(sin^(−1) a)))}]=What? 3.Prove that, sin [cot^(−1) {cos (tan^(−1) x)}]=(√((x^2 +1)/(x^2 +2))) 4.Mention Order and Degree and state also if it is linear or non-linear. y+(d^2 y/dx^2 )=((19)/(25))∫y^2 dx
$$\mathrm{1}.\left(\mathrm{i}\right)\mathrm{Evaluate}:\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}+\sqrt{\mathrm{2}}}{dx} \\ $$$$\left(\mathrm{ii}\right)\mathrm{Evaluate}:\int\mathrm{2}^{\mathrm{2}^{\mathrm{2}^{{x}} } } \mathrm{2}^{\mathrm{2}^{{x}} } \mathrm{2}^{{x}} \:{dx} \\ $$$$\left(\mathrm{iii}\right)\mathrm{Evaluate}:\int\frac{\mathrm{cos}\:^{\mathrm{3}} {x}}{\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{sin}\:{x}}{dx} \\ $$$$\mathrm{2}.\mathrm{cosec}\:\left[\mathrm{tan}^{−\mathrm{1}} \left\{\mathrm{cos}\:\left(\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{sec}\left(\mathrm{sin}^{−\mathrm{1}} {a}\right)\right)\right)\right\}\right]=\mathrm{What}? \\ $$$$\mathrm{3}.\mathrm{Prove}\:\mathrm{that},\:\:\mathrm{sin}\:\left[\mathrm{cot}^{−\mathrm{1}} \left\{\mathrm{cos}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)\right\}\right]=\sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}} \\ $$$$\mathrm{4}.\mathrm{Mention}\:\mathrm{Order}\:\mathrm{and}\:\mathrm{Degree}\:\mathrm{and}\:\:\mathrm{state}\:\mathrm{also}\:\mathrm{if}\:\mathrm{it}\:\mathrm{is}\:\mathrm{linear}\:\mathrm{or}\:\mathrm{non}-{l}\mathrm{inear}. \\ $$$$\:\:\:\:\:{y}+\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\mathrm{19}}{\mathrm{25}}\int{y}^{\mathrm{2}} \:{dx} \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
1) let I =∫ (dx/(sinx−cosx +(√2))) changement tan((x/2))=t give I =∫ (1/(((2t)/(1+t^2 ))−((1−t^2 )/(1+t^2 ))+(√2))) ((2dt)/(1+t^2 )) =∫ ((2dt)/(2t−1+t^2 +(√2)+(√2)t^2 )) = ∫ ((2dt)/((1+(√2))t^2 +2t +(√2)−1)) Δ^′ =1−(2−1) =0 ⇒one roots x_0 =((−b^′ )/a) =((−1)/(1+(√2))) ⇒ I =(1/(1+(√2))) ∫ ((2dt)/((t+(1/(1+(√2))))^2 ))+C =((−2)/((1+(√2))( t+(1/(1+(√2))))))+C =((−2)/((1+(√2))t +1)) +C =((−2)/(1+(1+(√2))tan((x/2)))) +C .
$$\left.\mathrm{1}\right)\:{let}\:{I}\:=\int\:\:\:\frac{{dx}}{{sinx}−{cosx}\:+\sqrt{\mathrm{2}}}\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\sqrt{\mathrm{2}}}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}{t}−\mathrm{1}+{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}{t}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}^{\mathrm{2}} +\mathrm{2}{t}\:+\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\Delta^{'} =\mathrm{1}−\left(\mathrm{2}−\mathrm{1}\right)\:=\mathrm{0}\:\Rightarrow{one}\:{roots}\:{x}_{\mathrm{0}} =\frac{−{b}^{'} }{{a}}\:=\frac{−\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\:\int\:\:\:\frac{\mathrm{2}{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }+{C}\:=\frac{−\mathrm{2}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left(\:{t}+\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)}+{C}\:=\frac{−\mathrm{2}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}\:+\mathrm{1}}\:+{C} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{1}+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){tan}\left(\frac{{x}}{\mathrm{2}}\right)}\:+{C}\:. \\ $$
Answered by Tanmay chaudhury last updated on 24/Jul/19
1)(1/( (√2)))∫(dx/(1+sin(x−(π/4)))) (1/( (√2)))∫((1−sin(x−(π/4)))/(cos^2 (x−(π/4))))dx (1/( (√2)))∫sec^2 (x−(π/4))−tan(x−(π/4))sec(x−(π/4)) dx (1/( (√2)))[tan(x−(π/4))−sec(x−(π/4))]+c
$$\left.\mathrm{1}\right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dx}}{\mathrm{1}+{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\mathrm{1}−{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{{cos}^{\mathrm{2}} \left({x}−\frac{\pi}{\mathrm{4}}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int{sec}^{\mathrm{2}} \left({x}−\frac{\pi}{\mathrm{4}}\right)−{tan}\left({x}−\frac{\pi}{\mathrm{4}}\right){sec}\left({x}−\frac{\pi}{\mathrm{4}}\right)\:\:\:{dx} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[{tan}\left({x}−\frac{\pi}{\mathrm{4}}\right)−{sec}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right]+{c} \\ $$
Commented by AnjanDey last updated on 24/Jul/19
Alter: I=∫(1/(sin x−cos x+(√2)))dx Here,sin x−cos x+(√2)=(√2)−(√2)((1/( (√2)))cos x−(1/( (√2)))sin x) =(√2){1−cos ((π/4)+x)} =2(√2)sin^2 ((π/2)+2x) =2(√2)cos^2 2x ∴I=∫(1/(2(√2)cos^2 2x))dx =(1/(2(√2)))∫sec^2 2x dx =(1/(2(√2)))∙((tan 2x)/2)+C (Where C= constant of integration) =(1/(4(√2)))tan 2x+C It may be easy method...
$$ \\ $$$$ \\ $$$${Alter}: \\ $$$$\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}+\sqrt{\mathrm{2}}}{dx} \\ $$$${Here},\mathrm{sin}\:{x}−\mathrm{cos}\:{x}+\sqrt{\mathrm{2}}=\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{cos}\:{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sin}\:{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}}\left\{\mathrm{1}−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+{x}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x} \\ $$$$\therefore\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}}{dx} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x}\:{dx} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\centerdot\frac{\mathrm{tan}\:\mathrm{2}{x}}{\mathrm{2}}+\mathrm{C}\:\:\left({Where}\:{C}=\:{constant}\:{of}\:{integration}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{tan}\:\mathrm{2}{x}+\mathrm{C}\: \\ $$$${It}\:{may}\:{be}\:{easy}\:{method}… \\ $$
Answered by Tanmay chaudhury last updated on 24/Jul/19
3)∫(((1−sin^2 x)cosxdx)/(sinx(1+sinx))) ∫(((1−sinx)cosxdx)/(sinx)) ∫(((1−t))/t)dt [t=sinx (dt/dx)=cosx] ∫(dt/t)−∫dt =lnt−t+c =ln(sinx)−sinx+c
$$\left.\mathrm{3}\right)\int\frac{\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right){cosxdx}}{{sinx}\left(\mathrm{1}+{sinx}\right)} \\ $$$$\int\frac{\left(\mathrm{1}−{sinx}\right){cosxdx}}{{sinx}} \\ $$$$\int\frac{\left(\mathrm{1}−{t}\right)}{{t}}{dt}\:\:\:\left[{t}={sinx}\:\:\:\frac{{dt}}{{dx}}={cosx}\right] \\ $$$$\int\frac{{dt}}{{t}}−\int{dt} \\ $$$$={lnt}−{t}+{c} \\ $$$$={ln}\left({sinx}\right)−{sinx}+{c} \\ $$
Answered by Tanmay chaudhury last updated on 24/Jul/19
3)tan^(−1) x=θ tanθ=x sin[cot^(−1) {cos(tan^(−1) x)}] =sin[cot^(−1) {cosθ}] let cot^(−1) (cosθ)=α cotα=cosθ=(1/( (√(1+x^2 )))) [since tanθ=x cosθ=(1/( (√(1+x^2 ))))] sin(α)=(1/(cosecα)) sinα=(1/( (√(1+cot^2 α))))=(1/( (√(1+(1/(1+x^2 )))))) sinα=((√(1+x^2 ))/( (√(2+x^2 ))))
$$\left.\mathrm{3}\right){tan}^{−\mathrm{1}} {x}=\theta\:\:\:\:{tan}\theta={x} \\ $$$${sin}\left[{cot}^{−\mathrm{1}} \left\{{cos}\left({tan}^{−\mathrm{1}} {x}\right)\right\}\right] \\ $$$$={sin}\left[{cot}^{−\mathrm{1}} \left\{{cos}\theta\right\}\right] \\ $$$${let}\:\:\:\:\:\:{cot}^{−\mathrm{1}} \left({cos}\theta\right)=\alpha \\ $$$${cot}\alpha={cos}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\:\:\:\left[{since}\:{tan}\theta={x}\:\:\:{cos}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right] \\ $$$${sin}\left(\alpha\right)=\frac{\mathrm{1}}{{cosec}\alpha} \\ $$$${sin}\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{cot}^{\mathrm{2}} \alpha}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }}} \\ $$$${sin}\alpha=\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }} \\ $$
Answered by Tanmay chaudhury last updated on 24/Jul/19
2)sin^(−1) a=θ secθ=(1/(cosθ))=(1/( (√(1−sin^2 θ))))=(1/( (√(1−a^2 )))) cosec[tan^(−1) {cos(cot^(−1) (sec(sin^(−1) a)))}] =cosec[tan^(−1) {cos(cot^(−1) ((1/( (√(1−a^2 ))))))}] cot^(−1) ((1/( (√(1−a^2 )))))=α cotα=(1/( (√(1−a^2 )))) so cosα=(1/( (√(2−a^2 )))) cosec[tan^(−1) {(1/( (√(2−a^2 ))))}] tanβ=(1/( (√(2−a^2 )))) →sinβ=(1/( (√(3−a^2 )))) cosec[tan^(−1) {tanβ}] cosecβ =(√(3−a^2 ))
$$\left.\mathrm{2}\right){sin}^{−\mathrm{1}} {a}=\theta \\ $$$${sec}\theta=\frac{\mathrm{1}}{{cos}\theta}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \theta}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }} \\ $$$${cosec}\left[{tan}^{−\mathrm{1}} \left\{{cos}\left({cot}^{−\mathrm{1}} \left({sec}\left({sin}^{−\mathrm{1}} {a}\right)\right)\right)\right\}\right] \\ $$$$={cosec}\left[{tan}^{−\mathrm{1}} \left\{{cos}\left({cot}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right)\right)\right\}\right] \\ $$$${cot}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right)=\alpha \\ $$$${cot}\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:\:\:{so}\:{cos}\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{a}^{\mathrm{2}} }} \\ $$$${cosec}\left[{tan}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{a}^{\mathrm{2}} }}\right\}\right] \\ $$$${tan}\beta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{a}^{\mathrm{2}} }}\:\:\rightarrow{sin}\beta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}−{a}^{\mathrm{2}} }} \\ $$$${cosec}\left[{tan}^{−\mathrm{1}} \left\{{tan}\beta\right\}\right] \\ $$$${cosec}\beta \\ $$$$=\sqrt{\mathrm{3}−{a}^{\mathrm{2}} }\: \\ $$
Answered by Tanmay chaudhury last updated on 24/Jul/19
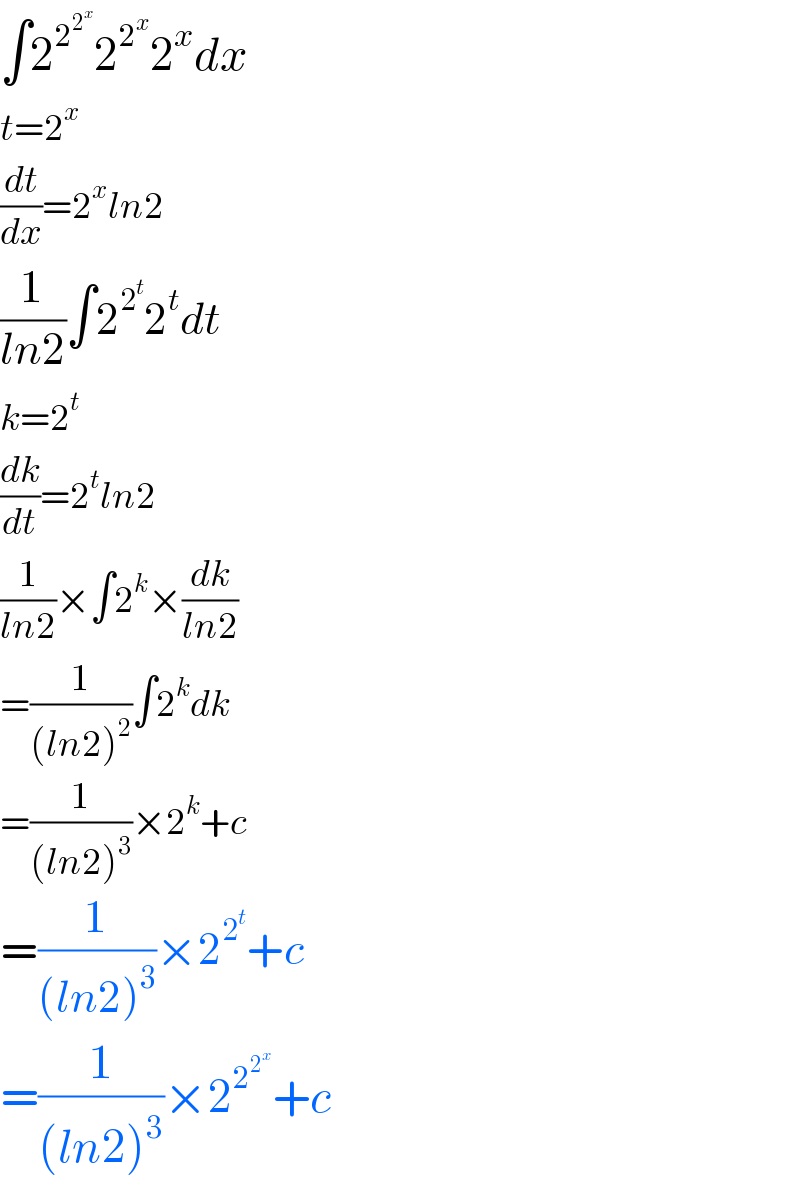
∫2^2^2^x 2^2^x 2^x dx t=2^x (dt/dx)=2^x ln2 (1/(ln2))∫2^2^t 2^t dt k=2^t (dk/dt)=2^t ln2 (1/(ln2))×∫2^k ×(dk/(ln2)) =(1/((ln2)^2 ))∫2^k dk =(1/((ln2)^3 ))×2^k +c =(1/((ln2)^3 ))×2^2^t +c =(1/((ln2)^3 ))×2^2^2^x +c
$$\int\mathrm{2}^{\mathrm{2}^{\mathrm{2}^{{x}} } } \mathrm{2}^{\mathrm{2}^{{x}} } \mathrm{2}^{{x}} {dx} \\ $$$${t}=\mathrm{2}^{{x}} \\ $$$$\frac{{dt}}{{dx}}=\mathrm{2}^{{x}} {ln}\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{ln}\mathrm{2}}\int\mathrm{2}^{\mathrm{2}^{{t}} } \mathrm{2}^{{t}} {dt} \\ $$$${k}=\mathrm{2}^{{t}} \\ $$$$\frac{{dk}}{{dt}}=\mathrm{2}^{{t}} {ln}\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{ln}\mathrm{2}}×\int\mathrm{2}^{{k}} ×\frac{{dk}}{{ln}\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\left({ln}\mathrm{2}\right)^{\mathrm{2}} }\int\mathrm{2}^{{k}} {dk} \\ $$$$=\frac{\mathrm{1}}{\left({ln}\mathrm{2}\right)^{\mathrm{3}} }×\mathrm{2}^{{k}} +{c} \\ $$$$=\frac{\mathrm{1}}{\left({ln}\mathrm{2}\right)^{\mathrm{3}} }×\mathrm{2}^{\mathrm{2}^{{t}} } +{c} \\ $$$$=\frac{\mathrm{1}}{\left({ln}\mathrm{2}\right)^{\mathrm{3}} }×\mathrm{2}^{\mathrm{2}^{\mathrm{2}^{{x}} } } +{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *