1-Integrate-F-x-y-x-2-over-the-region-bounded-by-y-x-2-x-2-and-x-1-2-Integrate-G-x-y-x-2-y-2-over-the-region-bounded-by-the-triangle-x-y-y-

Facebook Tweet Pin

Question Number 80914 by TawaTawa last updated on 07/Feb/20

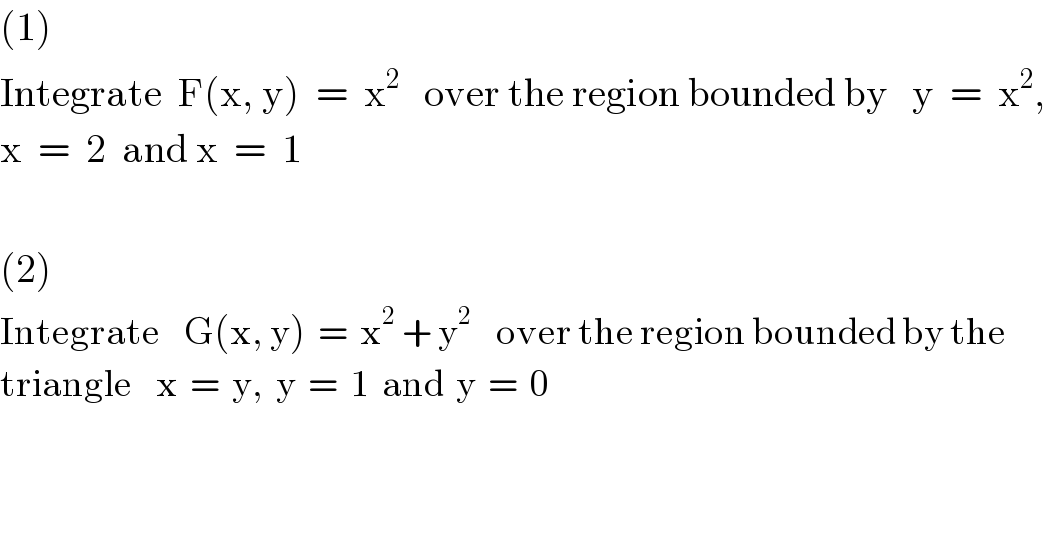
(1) Integrate F(x, y) = x^2 over the region bounded by y = x^2 , x = 2 and x = 1 (2) Integrate G(x, y) = x^2 + y^2 over the region bounded by the triangle x = y, y = 1 and y = 0

$$\left(\mathrm{1}\right) \\ $$$$\mathrm{Integrate}\:\:\mathrm{F}\left(\mathrm{x},\:\mathrm{y}\right)\:\:=\:\:\mathrm{x}^{\mathrm{2}} \:\:\:\mathrm{over}\:\mathrm{the}\:\mathrm{region}\:\mathrm{bounded}\:\mathrm{by}\:\:\:\mathrm{y}\:\:=\:\:\mathrm{x}^{\mathrm{2}} , \\ $$$$\mathrm{x}\:\:=\:\:\mathrm{2}\:\:\mathrm{and}\:\mathrm{x}\:\:=\:\:\mathrm{1} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{Integrate}\:\:\:\:\mathrm{G}\left(\mathrm{x},\:\mathrm{y}\right)\:\:=\:\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \:\:\:\:\mathrm{over}\:\mathrm{the}\:\mathrm{region}\:\mathrm{bounded}\:\mathrm{by}\:\mathrm{the}\: \\ $$$$\mathrm{triangle}\:\:\:\:\mathrm{x}\:\:=\:\:\mathrm{y},\:\:\mathrm{y}\:\:=\:\:\mathrm{1}\:\:\mathrm{and}\:\:\mathrm{y}\:\:=\:\:\mathrm{0} \\ $$

Facebook Tweet Pin

1-Integrate-F-x-y-x-2-over-the-region-bounded-by-y-x-2-x-2-and-x-1-2-Integrate-G-x-y-x-2-y-2-over-the-region-bounded-by-the-triangle-x-y-y-

Leave a Reply Cancel reply