Question Number 61915 by aseerimad last updated on 11/Jun/19

$$\mathrm{1}+{iw}+\left({iw}\right)^{\mathrm{2}} +\left({iw}\right)^{\mathrm{3}} +………\left({iw}\right)^{\mathrm{989}} =? \\ $$$$ \\ $$$${ans}=\:\:\:\:\frac{\mathrm{2}}{\mathrm{1}−{iw}}\:\:\:\:\:\:{answer}\:{is}\:{correct}. \\ $$$${pls}\:{help}\:..\:{how}\:{to}\:{do}\:{this}? \\ $$$${TIA} \\ $$
Answered by tanmay last updated on 11/Jun/19
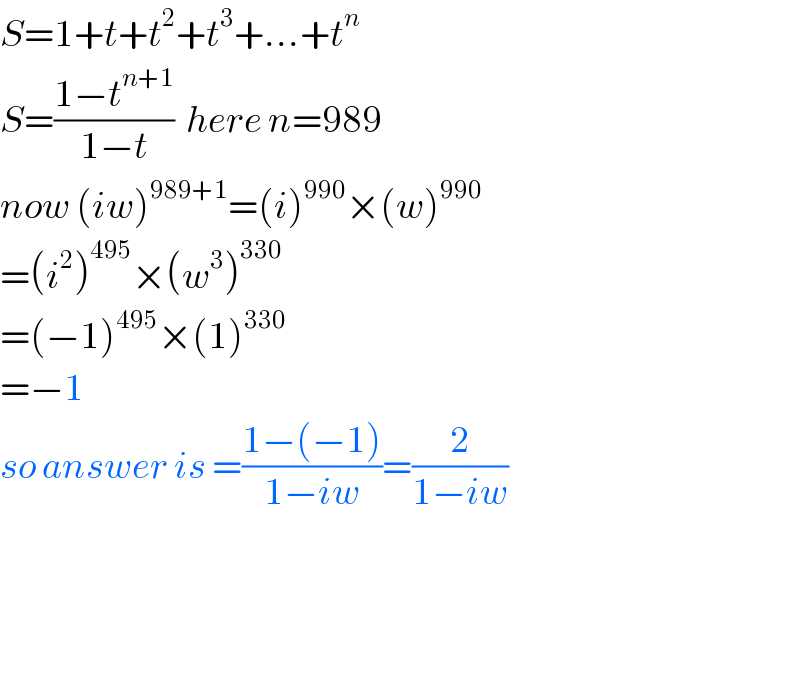
$${S}=\mathrm{1}+{t}+{t}^{\mathrm{2}} +{t}^{\mathrm{3}} +…+{t}^{{n}} \\ $$$${S}=\frac{\mathrm{1}−{t}^{{n}+\mathrm{1}} }{\mathrm{1}−{t}}\:\:{here}\:{n}=\mathrm{989} \\ $$$${now}\:\left({iw}\right)^{\mathrm{989}+\mathrm{1}} =\left({i}\right)^{\mathrm{990}} ×\left({w}\right)^{\mathrm{990}} \\ $$$$=\left({i}^{\mathrm{2}} \right)^{\mathrm{495}} ×\left({w}^{\mathrm{3}} \right)^{\mathrm{330}} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{495}} ×\left(\mathrm{1}\right)^{\mathrm{330}} \\ $$$$=−\mathrm{1} \\ $$$${so}\:{answer}\:{is}\:=\frac{\mathrm{1}−\left(−\mathrm{1}\right)}{\mathrm{1}−{iw}}=\frac{\mathrm{2}}{\mathrm{1}−{iw}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
