Question Number 127572 by mathocean1 last updated on 30/Dec/20
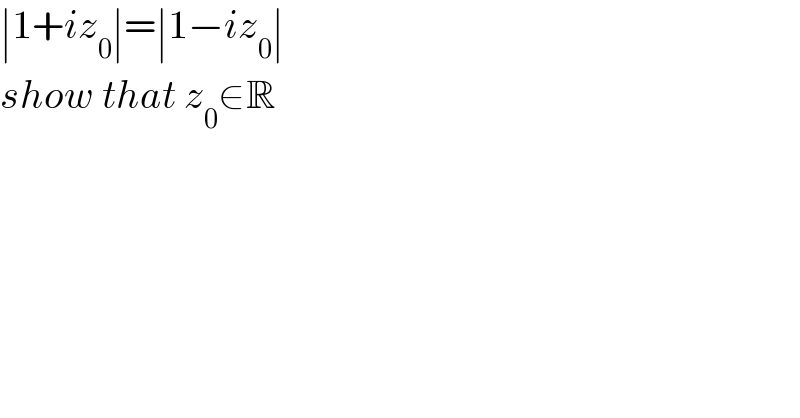
$$\mid\mathrm{1}+{iz}_{\mathrm{0}} \mid=\mid\mathrm{1}−{iz}_{\mathrm{0}} \mid \\ $$$${show}\:{that}\:{z}_{\mathrm{0}} \in\mathbb{R} \\ $$
Answered by mathmax by abdo last updated on 31/Dec/20
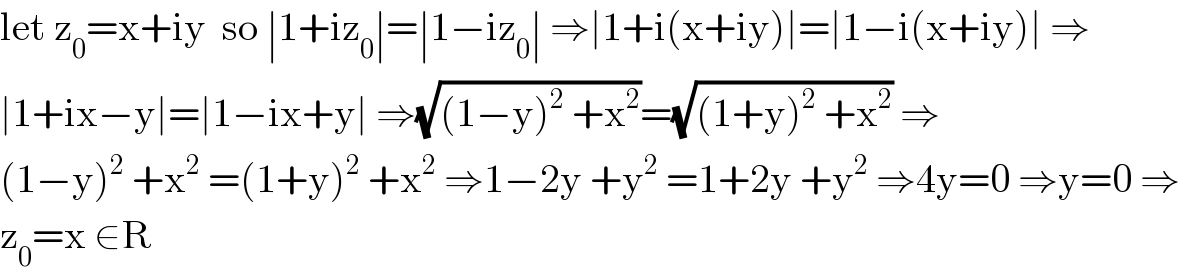
$$\mathrm{let}\:\mathrm{z}_{\mathrm{0}} =\mathrm{x}+\mathrm{iy}\:\:\mathrm{so}\:\mid\mathrm{1}+\mathrm{iz}_{\mathrm{0}} \mid=\mid\mathrm{1}−\mathrm{iz}_{\mathrm{0}} \mid\:\Rightarrow\mid\mathrm{1}+\mathrm{i}\left(\mathrm{x}+\mathrm{iy}\right)\mid=\mid\mathrm{1}−\mathrm{i}\left(\mathrm{x}+\mathrm{iy}\right)\mid\:\Rightarrow \\ $$$$\mid\mathrm{1}+\mathrm{ix}−\mathrm{y}\mid=\mid\mathrm{1}−\mathrm{ix}+\mathrm{y}\mid\:\Rightarrow\sqrt{\left(\mathrm{1}−\mathrm{y}\right)^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} }=\sqrt{\left(\mathrm{1}+\mathrm{y}\right)^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{y}\right)^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} \:=\left(\mathrm{1}+\mathrm{y}\right)^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{1}−\mathrm{2y}\:+\mathrm{y}^{\mathrm{2}} \:=\mathrm{1}+\mathrm{2y}\:+\mathrm{y}^{\mathrm{2}} \:\Rightarrow\mathrm{4y}=\mathrm{0}\:\Rightarrow\mathrm{y}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{z}_{\mathrm{0}} =\mathrm{x}\:\in\mathrm{R} \\ $$
