Question Number 39030 by maxmathsup by imad last updated on 01/Jul/18
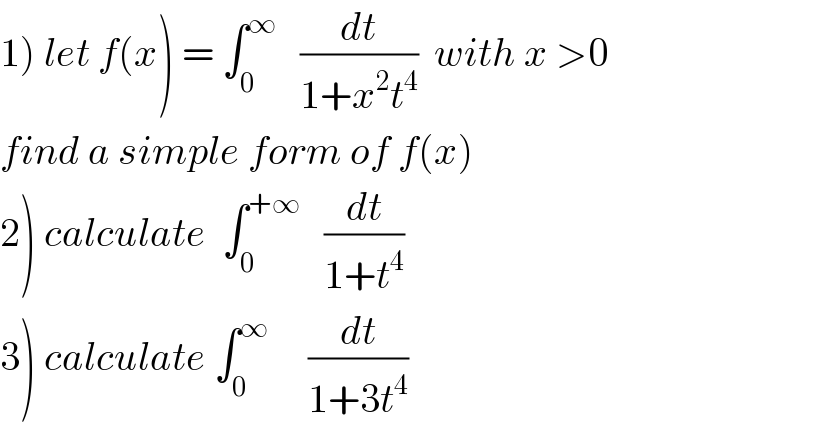
Commented by maxmathsup by imad last updated on 02/Jul/18

Commented by ajfour last updated on 02/Jul/18

Commented by maxmathsup by imad last updated on 02/Jul/18

Answered by behi83417@gmail.com last updated on 02/Jul/18
![(1−ixt^2 )(1+ixt^2 )=0 ⇒t^2 =(1/(ix)),−(1/(ix))⇒t=±(1/( (√(ix)))),((±i)/( (√(ix)))),(1/( (√(ix))))=m m=(1/( (√(ix))))=((√i)/(i(√x)))=−((ie^((iπ)/4) )/( (√x)))=−((i(((√2)/2)+i((√2)/2)))/( (√x)))=((1−i)/( (√(2x)))) I=∫(dt/((t−m)(t+m)(t−im)(t+im)))= (1/((t−m)(t+m)(t−im)(t+im)))= =(a/(t−m))+(b/(t+m))+(c/(t−im))+(d/(t+im)) a=(1/(2m.m^2 (1−i^2 )))=(1/(4m^3 )) b=(1/(−2m.m^2 (1−i^2 )))=((−1)/(4m^3 )) c=(1/(m(i−1)m(i+1)(2im)))=(i/(4m^3 )) d=(1/(−m(i+1)m(i−1)(2im)))=((−i)/(4m^3 )) I=(1/(4m^3 ))∫[(1/(t−m))−(1/(t+m))+(i/(t−im))−(i/(t+im))]dt =(1/(4m^3 ))[ln((t−m)/(t+m))+i.ln((t−im)/(t+im))]= =(1/(4m^3 ))[ln((t^2 −2mt+m^2 )/(t^2 −m^2 ))+i.ln((t^2 −2mit−m^2 )/(t^2 +m^2 ))]= =(1/(4.(((1−i)^3 )/(2x(√(2x))))))[ln((t^2 −2t((1−i)/( (√(2x))))+(i/x))/(t^2 −(i/x)))+i.ln((t^2 −2t((1+i)/( (√(2x))))−(i/x))/(t^2 +(i/x)))]= =−((x(√(2x)))/(4(2i+1)))[ln(((x(√(2x)).t^2 −2(1−i)xt+i.(√(2x)))/(xt^2 −i)))+ +i.ln(((x(√(2x)).t^2 −2(1+i)xt−i(√(2x)))/(xt^2 +i)))]+const. F(x)=F(∞)−F(0)=−((x(√(2x)))/(4(2i+1)))[ln(√(2x))+i.ln(√(2x))− −ln(−(√(2x)))−i.ln(−(√(2x)))]= =((−x(√(2x)))/(4(2i+1)))[ln(−1)+iln(−1)]= =((−x(√(2x)))/(4(−4−1)))(2i−1)(1+i).i𝛑=((−π.x(√(2x)))/(20))(3i+1) F(1)=((−π(√2))/(20))(3i+1) F((√3))=((−π(√(6(√3))))/(20))(3i+1) .](https://www.tinkutara.com/question/Q39046.png)
Answered by ajfour last updated on 02/Jul/18
![f(x)=(1/x^2 )∫_0 ^( ∞) (dt/(t^4 +((1/x))^2 )) let (1/x) = y f(x)=y^2 ∫((dt/t^2 )/(t^2 +(y^2 /t^2 ))) = (y/2)∫(([(1+(y/t^2 ))−(1−(y/t^2 ))]dt)/((t−(y/t))^2 +2y)) =(y/2)[∫(du/(u^2 +((√(2y)))^2 ))−∫^ (dv/(v^2 −((√(2y)))^2 ))] =(y/(2(√(2y))))tan^(−1) ((u/( (√(2y)))))−(y/(4(√(2y))))ln ∣((v−(√(2y)))/(v+(√(2y))))∣+c =(1/(2(√(2x))))tan^(−1) (((t−(1/(tx)))/( (√(2/x)))))∣_0 ^∞ −(1/(4(√(2x))))ln ∣((t+(1/(tx))−(√(2/x)))/(t+(1/(tx))+(√(2/x))))∣_0 ^∞ ⇒ f(x) = (π/(2(√(2x))))](https://www.tinkutara.com/question/Q39075.png)
Commented by ajfour last updated on 02/Jul/18

Commented by maxmathsup by imad last updated on 02/Jul/18

